- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад на тему Прогрессии в окружающей нас жизни
Содержание
- 1. Прогрессии в окружающей нас жизни
- 2. Актуальность исследования (Почему это важно для
- 3. Объект исследования: последовательности: арифметическая и геометрическая
- 4. Цель исследования:Установить картину возникновения понятия прогрессииВыявление интересных
- 5. Исторические сведения Прогрессия – «движение вперед» Первые
- 6. Последовательность ФибоначчиУ европейцев правило для нахождения суммы
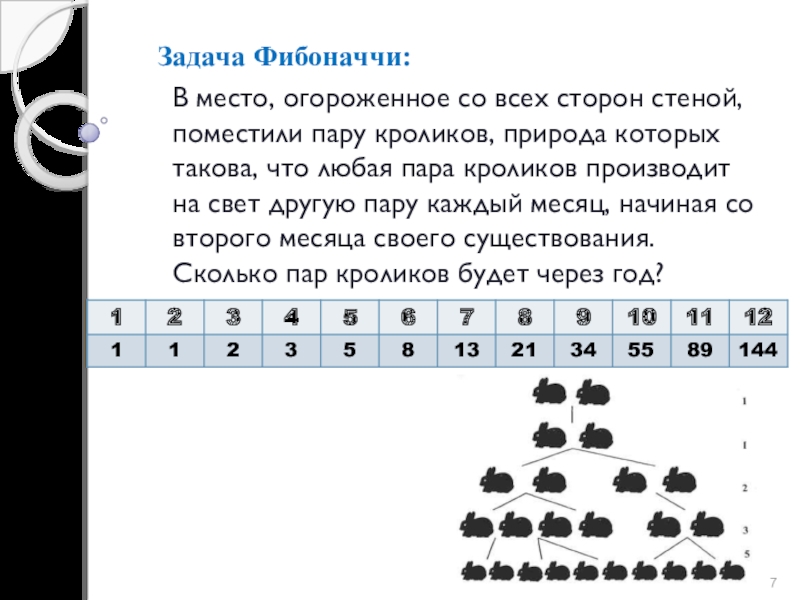
- 7. Задача Фибоначчи:В место, огороженное со всех сторон
- 8. «Сколько пар кроликов в один год от
- 9. Сведения из историиСами по себе прогрессии известны
- 10. Для того чтобы подсчитать величину награды, надо сложить зерна, лежащие на всех клеточках доски.
- 11. Решение:Дано: 1; 2; 4; 8; 16; …;b1=1;
- 12. Можно подсчитать, что масса такого числа пшеничных
- 13. Арифметическая прогрессия – последовательность, каждый член которой,
- 14. Геометрическая прогрессия –последовательность, первый член которой отличен
- 15. Задачи на применение прогрессий встречаются в старых учебниках по математике
- 16. Задача из арифметики Магницкого Некто продал лошадь
- 17. Решение:
- 18. «Давай, говорит, в течение месяца ябуду приносить
- 19. Слайд 19
- 20. Дано: b1=1; q=2Найти: S30 - ?РешениеS30 =
- 21. Сравним доходыКупец получил – 3 000 000
- 22. Имеют ли арифметическая и геометрическая прогрессии прикладное значение?
- 23. Задача № 614. Алгебра. 9 класс: Учебник
- 24. Задача № 471 Алгебра. 9 класс,
- 25. Задачи на прогрессииБольной принимает лекарство по следующей
- 26. Как сосчитать количество бревен?Представьте, что вы –
- 27. Задача. При хранении бревен строевого леса их
- 28. Интересные фактыХимия. При повышении температуры по арифметической
- 29. Когда сложное лучше простого?Существует две основные схемы
- 30. Прогрессии и банковские расчеты Рассмотрим конкретный пример.
- 31. Возведение многоэтажного здания — пример арифметической прогрессии.
- 32. О финансовых пирамидах: Разберёмся в механизмах этих
- 33. Прогрессии в природеИзвестно, что бактерии размножаются делением:
- 34. Задача №17.51 Алгебра. 9 класс, Ч.2.
- 35. Интенсивность размножения бактерий используют…
- 36. ВЫВОДЫ: В ходе выполнения данного исследования я:
- 37. Таким образом, поставленная цель проекта установить картину
- 38. Список использованных источниковАлгебра. 9 класс. В 2
Слайд 2Актуальность исследования
(Почему это важно для нас?)
В 9 классе мы изучаем
Слайд 3Объект исследования: последовательности: арифметическая и геометрическая прогрессии
Предмет исследования:
Гипотеза исследования: прогрессии имеют определенное практическое значение: сфер жизни человека, где встречаются прогрессии бесчисленное множество
Слайд 4Цель исследования:
Установить картину возникновения понятия прогрессии
Выявление интересных фактов о прогрессиях
Применение прогрессий
Методы исследования:
Поиск и анализ различных источников информации.
Систематизация и обобщение материалов исследования.
Слайд 5Исторические сведения
Прогрессия – «движение вперед»
Первые теоретические сведения, связанные с прогрессиями,
Пифагор (IV в. до н. э.) и его ученики рассматривали последовательности, связанные с геометрическими фигурами. Подсчитывая число кружков в треугольниках, квадратах, пятиугольниках, они получали:
- последовательность (аn) треугольных чисел 1; 3; 6; 10; 15; ... ;
- последовательность (bn) квадратных чисел 1; 4; 9; 16; 25; ... ;
- последовательность (cn) пятиугольных чисел 1; 5; 12; 22; 35; ... ;
Слайд 6Последовательность Фибоначчи
У европейцев правило для нахождения суммы членов любой арифметической прогрессии
«Книга об абаке» (1202 г.)
Слайд 7Задача Фибоначчи:
В место, огороженное со всех сторон стеной, поместили пару кроликов,
Слайд 8«Сколько пар кроликов в один год от одной пары родится».
Ряд чисел
Слайд 9Сведения из истории
Сами по себе прогрессии известны так давно, что конечно,
О том, как давно была известна геометрическая прогрессия, свидетельствует знаменитое предание о создании шахмат.
Индийский принц решил наградить изобретателя шахмат и предложил ему самому выбрать себе награду.
Изобретатель попросил в награду за первую клетку шахматной доски 1 зерно, за вторую — 2 зерна, за третью — 4 зерна и т. д. Каково же было удивление принца, когда он узнал, что такую, казалось бы, скромную просьбу невозможно выполнить.
Слайд 10Для того чтобы подсчитать величину награды, надо сложить зерна, лежащие на
Слайд 11Решение:
Дано: 1; 2; 4; 8; 16; …;
b1=1; n=64; q=2
Найти: S64 -
S64 = 264 - 1
Сумма равна: 18 446 744 073 709 551 615 - восемнадцать квинтильонов четыреста сорок шесть квадрильонов семьсот сорок четыре триллиона семьдесят три биллиона семьсот девять миллионов пятьсот пятьдесят одна тысяча шестьсот пятнадцать
Слайд 12Можно подсчитать, что масса такого числа пшеничных зёрен больше триллиона тонн.
Слайд 13Арифметическая прогрессия – последовательность, каждый член которой, начиная со второго, равен
Слайд 14Геометрическая прогрессия –последовательность, первый член которой отличен от нуля, а каждый
Слайд 16Задача из арифметики Магницкого
Некто продал лошадь за 156 рублей. Но
«Если по-твоему цена лошади высока, то купи ее подковные гвозди, лошадь же получишь тогда в придачу бесплатно. Гвоздей в каждой подкове 6. За первый гвоздь дай мне 1/4 коп., за второй - 1/2коп., за третий - 1коп., и т.д.»
Покупатель, соблазненный низкой ценой, и желая даром получить лошадь, принял условия продавца, рассчитывая, что за гвозди придется уплатить не более 10 рублей.
Слайд 18«Давай, говорит, в течение месяца я
буду приносить тебе каждое утро по
100
день отдашь 1 коп., а в каждый последующий в 2 раза больше. Во второй день - 2 коп.,
в третий - 4 коп. и т.д.»
Подумал купец и подписал договор.
Кому выгодна сделка?
Приходит как-то раз к одному богатому
купцу мужик и предлагает сделку.
Слайд 21Сравним доходы
Купец получил – 3 000 000 р.
Мужик – 10 737
Разница составляет – 7 737 418 руб. 23 коп.
Слайд 23Задача № 614. Алгебра. 9 класс: Учебник для общеобразовательных учреждений/ Макарычев Ю.Н.,
При свободном падении тело прошло в первую секунду 5м, а в каждую следующую на 10м больше. Найдите глубину шахты, если свободно падающее тело достигло его дна через 5с после начала падения.
Решение: Составим математическую модель задачи:
в первую секунду - 5м,
во вторую секунду - 15м,
в третью секунду - 25м,
в четвертую секунду - 35м,
в пятую секунду - 45м.
Всего за пять секунд - 5+15+25+35+45=125(м).
Ответ: глубина шахты 125м.
Слайд 24Задача № 471 Алгебра. 9 класс, в 2ч. Ч.2. Учебник для
Альпинисты в первый день восхождения поднялись на высоту 1400м, а затем каждый следующий день они проходи ли на 100м меньше, чем в предыдущий. За сколько дней они покорили высоту в 5000м?
Дано: 1400; 1300; …; a1=1400; d=-100; Sn=5000
Найти: n
Решение
Sn= (2a1+ d (n-1))n/2;
5000= (2·1400-100 · (n-1)) n/2;
10000= (2800-100 n+100) n;
10000= (2900-100 n) n;
100 n2-2900 n+10000=0;
n2-29 n+100=0;
n=25, n=4 – условию задачи удовлетворяет n=4 ( при n=25, аn=-1000, но аn>0)
Ответ: Значит, альпинисты покорили высоту за 4 дня.
Слайд 25Задачи на прогрессии
Больной принимает лекарство по следующей схеме: в первый день
Дано: 5; 10; 15; …; 40; 40; 40; 35; 30; …; 5
а1=5; d=5(возрастающая ар. пр.); а1=5; d=-5(убывающая ар. пр.)
Решение
а1 = а1+d(n-1)
40=5+5(n-1)
n = 8
Ответ: 2 пузырька лекарства
Слайд 26Как сосчитать количество бревен?
Представьте, что вы – учетчик на стройке. Привезли
В данном случае, чтобы подсчет бревен осуществлялся по простым формулам, один из способов – использовать естественное расположение бревен так, чтобы в каждом верхнем ряду их оказалось на единицу меньше, чем в нижнем. Тогда число бревен ряда образует арифметическую прогрессию и общее количество легко подчитывается по формуле суммы арифметической прогрессии с разностью, равной единице.
Слайд 27Задача. При хранении бревен строевого леса их укладывают как показано на
Решение. Составим математическую модель задачи: 1, 2, 3, 4,…,12. Это арифметическая прогрессия, а1=1, d=1,аn=12. Надо найти n.
аn=a1+d(n-1); 12=1+1(n-1); n=12.
Sn=(a1+an)∙n:2; Sn=(1+12)·12:2; Sn=78.
В одной кладке находится 78 бревен.
Ответ: 78 бревен.
Слайд 28Интересные факты
Химия. При повышении температуры по арифметической прогрессии скорость химических реакций
Геометрия. Вписанные друг в друга правильные треугольники образуют геометрическую прогрессию.
Физика. И в физических процессах встречается эта закономерность. Нейтрон, ударяя по ядру урана, раскалывает его на две части. Получаются два нейтрона. Затем два нейтрона, ударяя по двум ядрам, раскалывает их еще на 4 части и т.д. – это геометрическая прогрессия.
Биология. Микроорганизмы размножаются делением пополам, поэтому при благоприятных условиях, через одинаковый промежуток времени их число удваивается.
Экономика. Вклады в банках увеличиваются по схемам сложных и простых процентов. Простые проценты – увеличение первоначального вклада в арифметической прогрессии, сложные проценты – увеличение в геометрической прогрессии.
Слайд 29Когда сложное лучше простого?
Существует две основные схемы наращивания капитала:
- схема
- схема сложных процентов.
Опустим все экономические сложности и покажем, в чём отличие между простыми и сложными процентами. Если проценты простые, то это значит, что деньги за определённый период времени будут начисляться на изначальную сумму вклада. Вклад со сложным процентом отличается от предыдущего тем, что проценты приписываются к первоначальному вкладу (капитализируются) через определенный период и затем, через следующий период, проценты уже начисляются на всю сумму.
В схемах простых и сложных процентов несложно заметить закономерности. Цепочка чисел, образующаяся при начислении простых процентов, составляет арифметическую прогрессию. Действительно, каждая сумма, начиная со второй, больше предыдущей на одно и то же количество денег. А при начислении сложных процентов сумма возрастает в геометрической прогрессии, так как каждая, начиная со второй, больше предыдущей в одно и то же число.
Это наглядный пример того, что знание арифметической и геометрической прогрессий помогает человеку, облегчает ему жизнь.
Слайд 30Прогрессии и банковские расчеты
Рассмотрим конкретный пример.
Пусть вклад
хранения вклада - 5 лет. Если вы выбрали стратегию простых
процентов, то к концу срока хранения вы получите в итоге сумму,
равную10 000 • (1 + ) , т. е. 15 000 р. Если же вы выбрали стратегию
сложных процентов, то к концу срока хранения вы получите
в итоге сумму, равную 10 000 • ( 1 + )5, т. е. 16 105,1 р.
Как говорится в одном рекламном слогане, почувствуйте разницу.
Алгебра. 9 класс, в 2ч. Ч.1. Учебник для
общеобразовательных учреждений/ Мордкович А.Г.,
П.В. Семенов ,-М.:Мнемозина,2010,-224с.(с.169-171)
Слайд 31Возведение многоэтажного здания — пример арифметической прогрессии. Каждый раз высота здания
Равноускоренное движение — арифметическая прогрессия, т.к. за каждые промежутки времени тело увеличивает скорость в одинаковое число раз.
Технические задачи: После каждого движения поршня разрежающего насоса из сосуда удаляется 20% находящегося в нём воздуха. Определите давление воздуха внутри сосуда, после 6 движений поршня, если первоначально давление было 760 мм. рт. ст.
В каких процессах ещё встречаются такие закономерности?
Слайд 32О финансовых пирамидах:
Разберёмся в механизмах этих организаций. Организатор начинает вовлекать в
Решение. Дело в том, что число участников увеличивается в 5 раз с каждым кругом. Если пятёрка устроителей подпишет, допустим, 120 человек со своими адресами, то в первом круге участвуют 120 человек, во втором – 600, в третьем – 3 000, …, в десятом – 234 375 000 человек; это намного больше населения страны. Так что участник, включившийся в восьмом или девятом круге, уже ничего не получит.
Слайд 33Прогрессии в природе
Известно, что бактерии размножаются делением: одна бактерия делится на
Слайд 34Задача №17.51 Алгебра. 9 класс, Ч.2. Учебник для общеобразовательных учреждений/ Мордкович
Бактерия, попав в живой организм, к концу 20-й минуты делится на две бактерии, каждая из них к концу следующих 20 минут делится опять на две и т.д. Найдите число бактерий, образующихся из одной бактерии к концу суток.
Решение:
В сутках 1 440 минут, каждые двадцать минут появляется новое поколение - за сутки 72 поколения. По формуле суммы n первых членов геометрической прогрессии, у которой b1=1, q=2, n=72, находим, что S72=272-1= 4 722 366 482 869 645 213 696 - 1=
= 4 722 366 482 869 645 213 695.
Слайд 36ВЫВОДЫ: В ходе выполнения данного исследования я:
установила, что сами по
убедилась в том, что задачи на прогрессии, дошедшие до нас из древности, также как и многие другие знания по математике, были связаны с запросами хозяйственной жизни: распределение продуктов, деление наследства и др.;
выяснила, что в развитие теории о прогрессиях внесли ученые Архимед, Пифагор и его ученики, французский математик Леонард Фибоначчи;
нашла много задач на арифметическую и геометрическую прогрессию в старых и в современных учебниках по математике. Заметили, что арифметическая прогрессия в практических задачах встречается чаще геометрической;
сделав анализ задач на прогрессии с практическим содержанием я увидела, что прогрессии встречаются при решении задач в медицине, в строительстве, в банковских расчетах, в живой природе, в спортивных соревнованиях и в других жизненных ситуациях;
следовательно, нам необходим навык применения знаний, связанных с прогрессиями.
Слайд 37Таким образом, поставленная цель проекта установить картину возникновения понятия прогрессии; выявление
Слайд 38Список использованных источников
Алгебра. 9 класс. В 2 ч. Ч.1. Учебник для
Алгебра. 9 класс. Учебник для общеобразовательных учреждений/ Ю.Н. Макарычев и др. под ред. С.А. Теляковского –М.: Просвещение, 2009 – 271 с.;
Алгебра. 9 класс, : Учебник для общеобразовательных учреждений / Макарычев Ю.Н., Миндюк Н.Г., Нешков К.И., Феактистов И.Е. . -М.: Мнеозина, 2008, -447с. № 698, 699,702,725,734, 788, 789 (7 задач)
Математика. Алгебра. Функции. Анализ данных.9 кл.: Учебник для общеобразовательных учебных заведений/ Г.В. Дорофеев , С.Б. Суворова, Е.А. Бунимович, Л.В. Кузнецова, С.С. Минаева; под ред. Г.В. Дорофеева. -М. :Дрофа, 2000,-352с.;
Пичурин Л.Ф. За страницами учебника алгебры. Книга для учащихся 7-9 классов средней школы -М.: Просвещение, 1990.-224сю;
Энциклопедический словарь юного математика /Сост. А.П.Савин.- М.: Педагогика, 1989.-352с..
http://n-t.ru/tp/iz/zs.htm
http://students.tspu.ru/students/legostaeva/index.php?page=op
http://festival.1september.ru/articles/568100/