- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад на тему Проектно-исследовательская работа по геометрии
Содержание
- 1. Проектно-исследовательская работа по геометрии
- 2. План. I. Введение. II.
- 3. I. Введение: Великий древнегреческий мыслитель
- 4. Слайд 4
- 5. Поставленные задачиИзучение основных свойств, формул, теорем и
- 6. II. Основная часть: Свойства и формулы метода
- 7. Решение геометрических задач Задача 1
- 8. Задача 2 В треугольнике ABC точка
- 9. Задача 3 В треугольнике АВС точка
- 10. III. Построение геометрических моделей.
- 11. Теория нахождения центроидов различных геометрических фигур
- 12. Центры тяжести окружности, площади круга,
- 13. Создание собственных моделей Нахождение центра тяжести прямоугольного треугольника
- 14. Нахождение центра тяжести тупоугольного треугольника
- 15. Нахождение центра тяжести остроугольного треугольника
- 16. Нахождение центра тяжести произвольного четырехугольника
- 17. IV. Заключение. Работая над проектом, я
Слайд 2План.
I. Введение.
II. Основная часть.
Определение центра
Свойства и формулы метода масс
Основной принцип решения геометрических задач
Решение задач
III. Построение геометрических моделей.
Теория нахождения центроидов различных геометрических фигур
Создание собственных моделей
IV. Заключение.
Слайд 3I. Введение:
Великий древнегреческий мыслитель Архимед открыл оригинальный
Слайд 5Поставленные задачи
Изучение основных свойств, формул, теорем и принципов использования метода масс.
Изучение
Применение полученных результатов для решения задач разного уровня сложности.
Построение моделей для наглядного представления центра масс системы материальных точек
Слайд 6II. Основная часть:
Свойства и формулы метода масс:
Любая система материальных точек имеет
Система из двух материальных точек имеет центр масс, принадлежащий отрезку, соединяющему эти точки, его положение определяется правилом рычага: m1d1=m2d2
Если в системе, состоящей из конечного числа материальных точек, отметить несколько точек и массы всех отмеченных точек перенести в их центр масс, то от этого положение центра масс всей системы не изменится
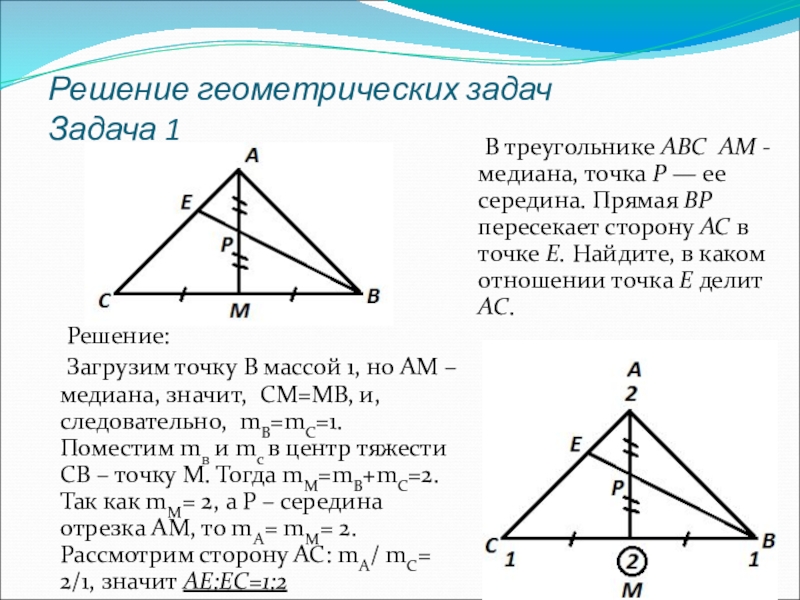
Слайд 7Решение геометрических задач
Задача 1
В треугольнике ABC AM -
Решение:
Загрузим точку В массой 1, но АМ – медиана, значит, СМ=МВ, и, следовательно, mВ=mC=1. Поместим mв и mс в центр тяжести СВ – точку М. Тогда mM=mB+mC=2. Так как mM= 2, а Р – середина отрезка АМ, то mА= mM= 2. Рассмотрим сторону АС: mА/ mC= 2/1, значит АЕ:ЕС=1:2
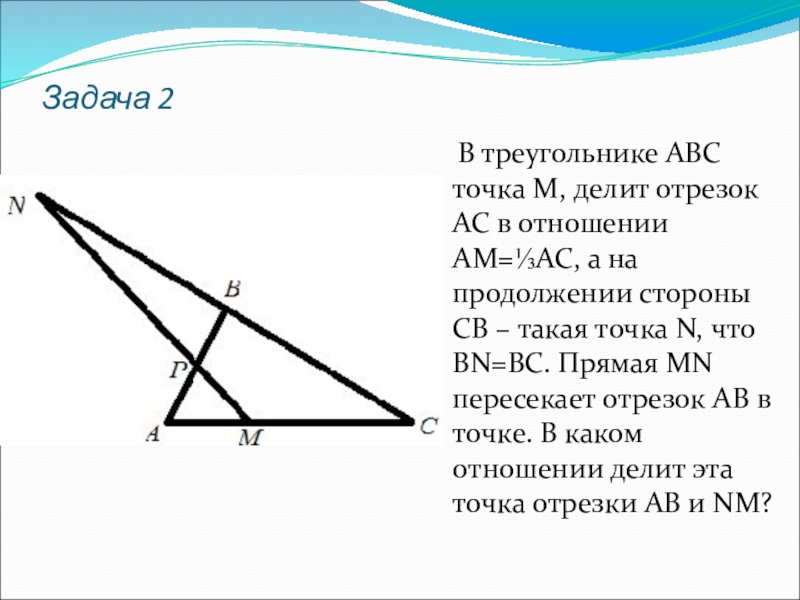
Слайд 8Задача 2
В треугольнике ABC точка M, делит отрезок АС
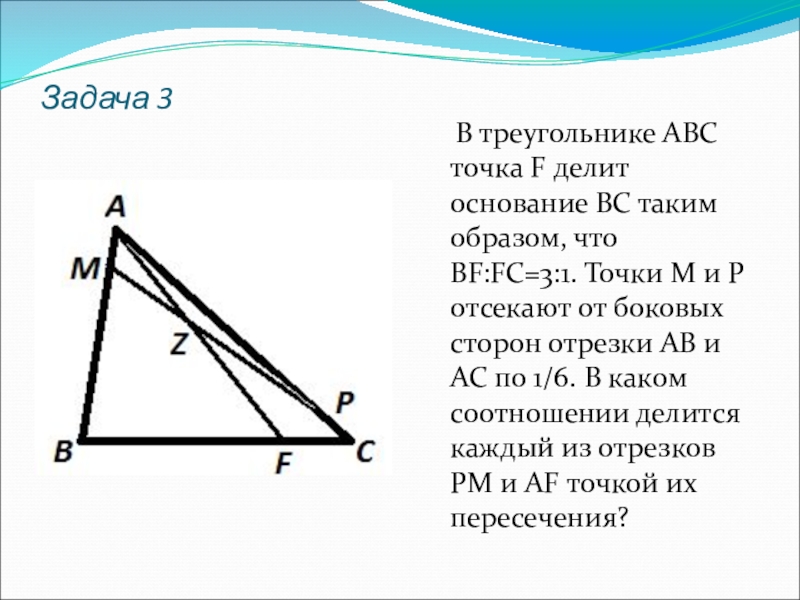
Слайд 9Задача 3
В треугольнике АВС точка F делит основание ВС
Слайд 11Теория нахождения центроидов различных геометрических фигур
Центр тяжести любого треугольника
Диагональ трапеции разделяет трапецию на два треугольника. Центр тяжести трапеции находится в точке пересечения линии, соединяющей центры тяжести этих треугольников, и средней линии трапеции, соединяющей ее основания.
Слайд 12 Центры тяжести окружности, площади круга, поверхности и объема шара
Центр тяжести правильного многоугольника находится в центре вписанной (или описанной) окружности.
Центры тяжести параллелограмма, ромба, прямоугольника и квадрата лежат в точках пересечения их диагоналей
Слайд 17IV. Заключение.
Работая над проектом, я изучила новый для меня
На основе проведенных исследований, можно сделать вывод, что применение метода масс при решении геометрических задач может намного облегчить ход решений