Номинация: «Хочу все знать»
Руководитель проекта: Аверина Л.В., учитель математики.
Автор проекта - Аверина Маргарита, ученица 8 класса.
- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад на тему Проектная работа Изгибаемые многогранники
Содержание
- 1. Проектная работа Изгибаемые многогранники
- 2. Цель: познакомиться с изгибаемыми многогранниками
- 3. План 1. Постановка задачи 2. Из истории
- 4. Герберт Спенсер сравнивал процесс познания с расширяющейся
- 5. На первых уроках геометрии в 8 классе
- 6. Многогранник называется изгибаемым,
- 7. В 1813 Огюстен Луи Коши опубликовал работу
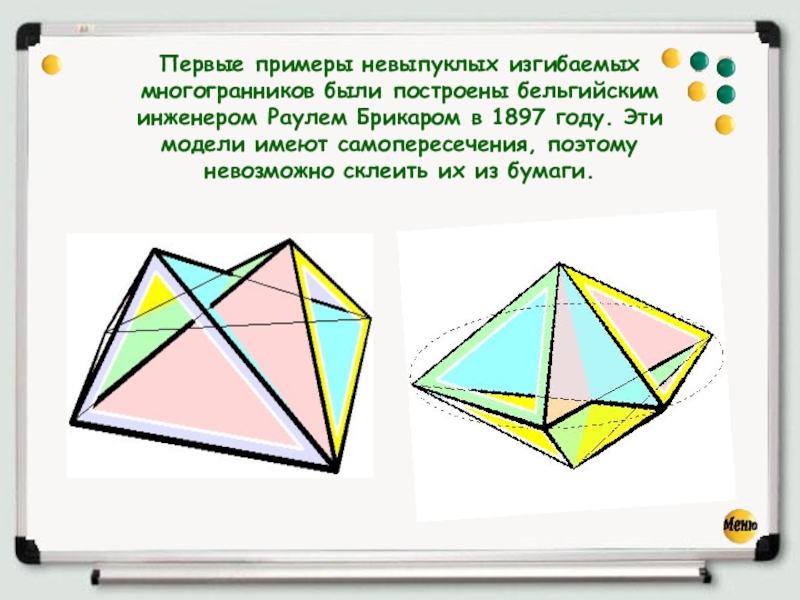
- 8. Первые примеры невыпуклых изгибаемых многогранников были построены
- 9. Только в 1976 году американский математик Роберт Коннелли построил достаточно сложный изгибаемый многогранник без самопересечений.
- 10. Роберт Коннелли исследовал жёсткость, устойчивость и изгибаемость
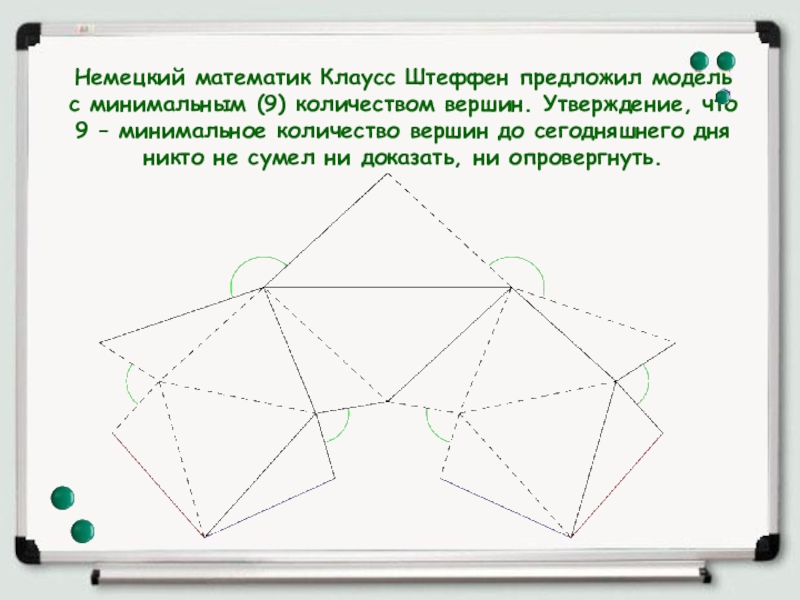
- 11. Немецкий математик Клаусс Штеффен предложил модель с
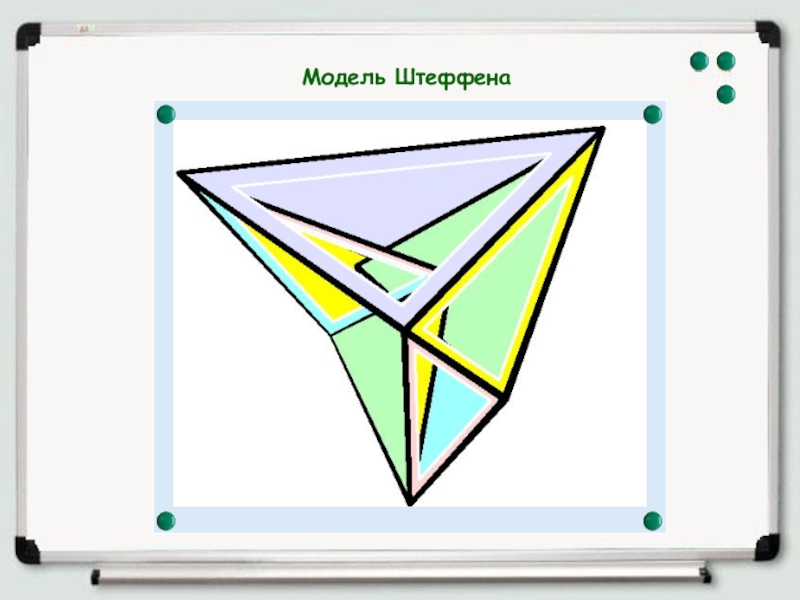
- 12. Модель Штеффена
- 13. Я попыталась склеить многогранник Штеффена Практика показала, что для модели нужно выбрать максимально плотный картон
- 14. Дж.М. Андреас и Р.М. Сталкер независимо друг
- 15. Если расположить числа от 1 до 32
- 16. При n=6 фигура достаточно жесткаяn=8Фигура может изгибаться
- 17. Очевидно, что в процессе вращения, объем флексоров
- 18. Проведем эксперимент. Поскольку трудно сделать картонные модели
- 19. В 1996 году Иджад Хакович Сабитов,
- 20. Никколо Тарталья через длины ребер выразил объем
- 21. Теорема Сабитова устанавливает связь между длинами
- 22. На одной из западных научных выставок
- 23. Изучая статью Александрова В.А. «Изгибаемые многогранные
- 24. По пунктирным линиям развертку многогранника нужно согнуть
- 25. Измерю объем получившихся фигур полюбившимся мне способом…300 мл400 мл
- 26. Применение теории изгибаемых многогранниковСтроительство (увеличение/ уменьшение
- 27. При изучении многогранников мне удалось прикоснуться к
- 28. Литература -У. Болл, Г. Коксетер. Математические
Слайд 1ГОУ – основная общеобразовательная школа с углубленным изучением иностранного языка при
Слайд 2Цель:
познакомиться с изгибаемыми многогранниками
_______________________________________
Задачи:
-развивать пространственное мышление;
-учиться работать с научным текстом;
-учиться работать с графической информацией различного типа, создавать анимированные изображения.
_______________________________________
Слайд 3План
1. Постановка задачи
2. Из истории проблемы
3. Модели изгибаемых многогранников
4.Гипотеза
5. Применение теории изгибаемых многогранников
6. Вывод
_________________________________
Слайд 4
Герберт Спенсер сравнивал процесс познания с расширяющейся сферой: внутренность сферы заполнена
__________________________________
Вопрос об изгибаемых многогранниках – яркий тому пример
Слайд 5На первых уроках геометрии в 8 классе мы познакомились с многоугольниками
А можно ли деформировать, изогнуть многогранник?
Слайд 6
Многогранник называется изгибаемым,
Слайд 7
В 1813 Огюстен Луи Коши опубликовал работу «О многоугольниках и многогранниках»,
После знакомства с этой работой немецкий математик Феликс Клейн сказал: «По блестящим достижениям во всех областях математики Коши можно поставить почти рядом с Гауссом»
Эта оценка очень весома, особенно если учесть, что взаимоотношения между французскими и немецкими математиками развивались в атмосфере острой конкуренции, и признание заслуг соперников никогда не отличалось щедростью.
_______________________
Слайд 8Первые примеры невыпуклых изгибаемых многогранников были построены бельгийским инженером Раулем Брикаром в
Слайд 9Только в 1976 году американский математик Роберт Коннелли построил достаточно сложный
Слайд 10
Роберт Коннелли исследовал жёсткость, устойчивость и изгибаемость многогранников и каркасов.
Он решил
Открытию изгибаемого многогранника без самопересечений был посвящён доклад на Международном математическом конгрессе, который Коннелли сделал в Хельсинки в 1978 году. Одна из моделей изгибаемого многогранника находится в Национальном музее американской истории
Слайд 11Немецкий математик Клаусс Штеффен предложил модель с минимальным (9) количеством вершин.
Слайд 13
Я попыталась склеить многогранник Штеффена
Практика показала, что для модели нужно
Слайд 14Дж.М. Андреас и Р.М. Сталкер независимо друг от друга открыли семейство
Гранями служат грани n тетраэдров, соединенных между собой в циклическом порядке по определенным парам противоположных ребер каждого, так что получается фигура наподобие кольца.
Слайд 15Если расположить числа от 1 до 32 так, как показано на
Развертка для флексора при n=10
Слайд 16
При n=6 фигура достаточно жесткая
n=8
Фигура может изгибаться и поворачиваться
n=10
На мой
n=12
«Раскрыть» фигуру полностью не удается, при n>22 она заузливается
Слайд 17Очевидно, что в процессе вращения, объем флексоров не меняется. А меняется
Роберт Коннелли назвал предположение о постоянстве объёма изгибаемого многогранника в ходе его изгибания «гипотезой кузнечных мехов».
Слайд 18Проведем эксперимент. Поскольку трудно сделать картонные модели герметичными, наполним два многогранника
>
<
=
Объемы оказались равными!
Слайд 19
В 1996 году Иджад Хакович Сабитов, преподаватель
Герон Александрийский
Тарталья (Niccolò Fontana Tartaglia)
Сабитов И.Х.
Слайд 20Никколо Тарталья через длины ребер выразил объем тетраэдра:
V2=1/144*(l12l52 (l22+l32+l42+l62-l12-l52)+(l22l62 (l12+l32+l42+l52-l22-l62)+(l32l42 (l12+l22+l52+l62-l32-l42)-l12l22l42-l22l32l52-l12l32l62-l42l52l62))
По
a
b
c
l1
l2
l3
l4
l5
l6
Слайд 21
Теорема Сабитова устанавливает связь между длинами рёбер любого, не обязательно
Существует такой многочлен одной переменной, что его коэффициенты зависят только от длин рёбер многогранника, а объём есть корень этого многочлена. Так как рёбра у изгибаемых многогранников не меняются, то и сам этот многочлен, а значит, и его корни не меняются при изгибании самого многогранника.
При малых деформациях многогранника объём может меняться мало, поэтому не может резко перепрыгнуть из одного корня многочлена в другой. Значит, объём изгибаемых многогранников не меняется при их изгибаниях!
______________________________________
Слайд 22
На одной из западных научных выставок произошел казус. Демонстрировалась модель
Но позже выяснилось, что в математическом смысле модель неизгибаема, а ее "изгибания" - следствие растяжения материала.
Были предприняты попытки опровержения теории о постоянстве объемов путём построения контрпримеров.
Слайд 23
Изучая статью Александрова В.А. «Изгибаемые многогранные поверхности», я с удивлением
Для примера возьмем пакет молока, имеющий изначально форму правильного тетраэдра (в 70-е годы именно такие пакеты были распространены в нашей стране повсеместно).
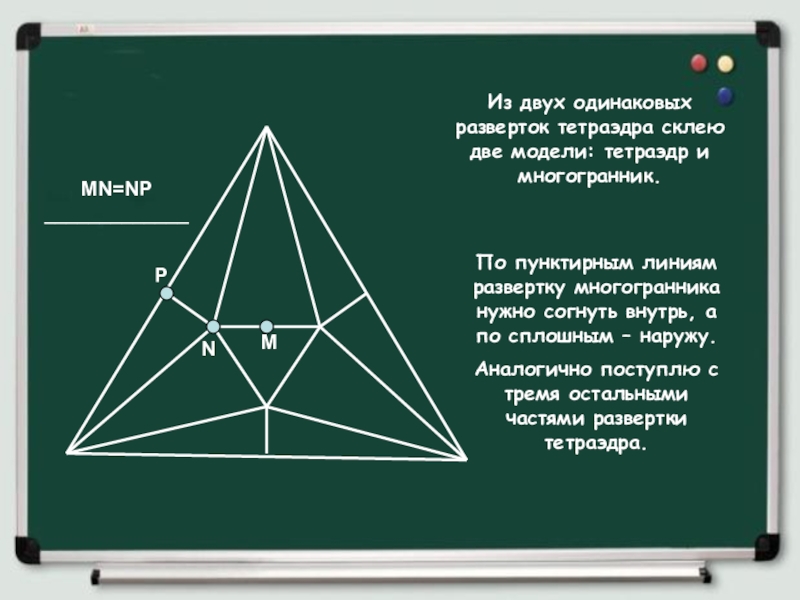
Слайд 24По пунктирным линиям развертку многогранника нужно согнуть внутрь, а по сплошным
Аналогично поступлю с тремя остальными частями развертки тетраэдра.
M
N
P
MN=NP _____________
Из двух одинаковых разверток тетраэдра склею две модели: тетраэдр и многогранник.
Слайд 26
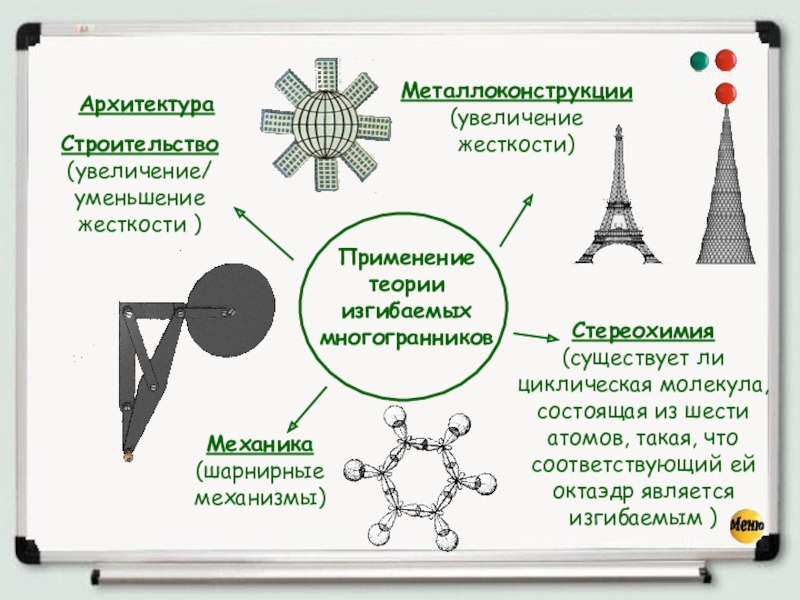
Применение теории изгибаемых многогранников
Строительство (увеличение/ уменьшение жесткости )
Стереохимия (существует ли
Механика (шарнирные механизмы)
Архитектура
Металлоконструкции (увеличение жесткости)
Слайд 27
При изучении многогранников мне удалось прикоснуться к одной из современных проблем
Эта тема интересна тем, что теорию можно поверить достаточно простыми практическими способами. Постановка задач понятна даже школьнику, но до сих пор некоторые проблемы не решены учеными. Например,
вопрос об изменении или постоянстве объёма изгибаемых многогранников в пространствах размерности 4 до сих пор не решён и ждёт своего исследователя.
Слайд 28
Литература
-У. Болл, Г. Коксетер. Математические эссе и развлечения. Пер.
-Н. П. Долбилин. Жемчужины теории многогранников. "Библиотека «Математическое просвещение»«, выпуск 5
-http://www.pereplet.ru/obrazovanie/stsoros/331.html
-Часть 1 // Квант. 2001. N 5. С. 7-12.
-Часть 2 // Квант. 2001. N 6. С. 3-10.
-И.Х. Сабитов. Объёмы многогранников. — М.: МЦНМО, 2002
-Александров В.А. Изгибаемые многогранные поверхности // Соросовский Образовательный Журнал. 1997. № 5. С. 112-117