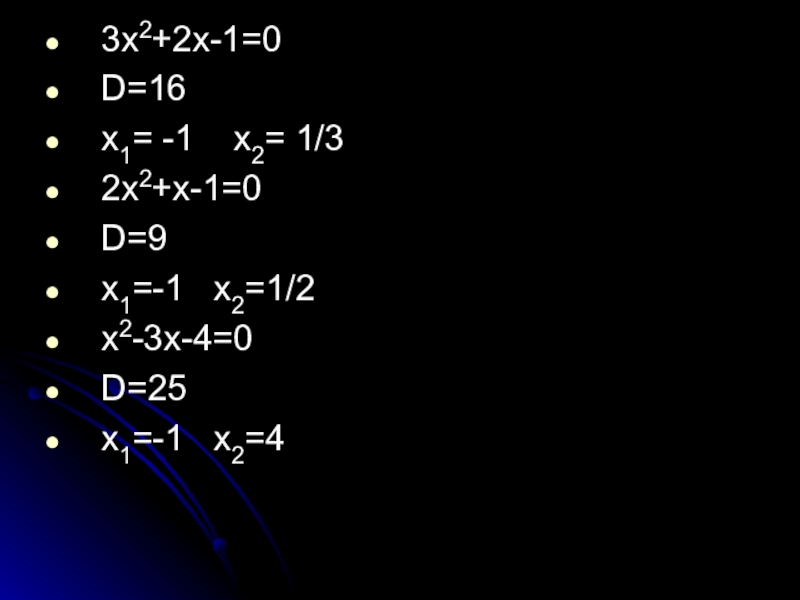- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад на тему Проект учащихся по теме Квадратные уравнения
Содержание
- 1. Проект учащихся по теме Квадратные уравнения
- 2. Квадратные уравненияОпределение 1. Квадратным уравнением называют уравнение
- 3. Определение 2. Корнем квадратного уравнения ax2+bx+c=0 называют
- 4. Определение 3. Полное квадратное уравнение – это
- 5. Определение 4. Для приведенного квадратного уравнения x2+px+q=0 сумма корней равна -p, а произведение корней равно q.
- 6. Особые квадратные уравнения:2x2-x-1=0D=9x1=1 x2=-1 ∕22x2+3x-5=0D=49x1=1 x2=-5∕2x2+3x-4=0D=25x1=1 x2= -4
- 7. 3x2+2x-1=0D=16x1= -1 x2= 1/32x2+x-1=0D=9x1=-1 x2=1/2x2-3x-4=0D=25x1=-1 x2=4
Квадратные уравненияОпределение 1. Квадратным уравнением называют уравнение вида ax2+bx+c=0, где коэффициенты a,b,c- любые действительные числа, причем а≠0. Многочлен ax2+bx+c называют квадратным трехчленом.
Слайд 2Квадратные уравнения
Определение 1. Квадратным уравнением называют уравнение вида ax2+bx+c=0, где коэффициенты
a,b,c- любые действительные числа, причем а≠0.
Многочлен ax2+bx+c называют квадратным трехчленом.
Многочлен ax2+bx+c называют квадратным трехчленом.
Слайд 3Определение 2. Корнем квадратного уравнения ax2+bx+c=0 называют всякое значение переменной x,
при котором квадратный трехчлен ax2+bx+c обращается в нуль; такое значение переменной x называют также корнем квадратного трехчлена.
Квадратные уравнения с коэффициентами a, b, c могут иметь от 0 до двух корней, либо вообще не иметь корней в зависимости от значения дискриминанта.
Решить квадратное уравнение –значит найти все его корни или установить ,что корней нет.
Квадратные уравнения с коэффициентами a, b, c могут иметь от 0 до двух корней, либо вообще не иметь корней в зависимости от значения дискриминанта.
Решить квадратное уравнение –значит найти все его корни или установить ,что корней нет.
Слайд 4Определение 3. Полное квадратное уравнение – это квадратное уравнение, в котором
присутствуют все три слагаемых; иными словами, это уравнение, у которого коэффициенты b и c отличны от нуля. Неполное квадратное уравнение – это уравнение, в котором присутствуют не все три слагаемых; иными словами, это уравнение, у которого хотя бы один коэффициентов b,c равен нулю. Приведенное квадратное уравнение – это квадратное уравнение, в котором а=1.
Слайд 5Определение 4. Для приведенного квадратного уравнения x2+px+q=0 сумма корней равна -p,
а произведение корней равно q.
Слайд 6Особые квадратные уравнения:
2x2-x-1=0
D=9
x1=1 x2=-1 ∕2
2x2+3x-5=0
D=49
x1=1 x2=-5∕2
x2+3x-4=0
D=25
x1=1 x2= -4
