МОУ Непецинская СОШ
- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад на тему Проект Решение задач при помощи электронных таблиц
Содержание
- 1. Проект Решение задач при помощи электронных таблиц
- 2. Целью моей работы было рассмотреть задачи, решаемых
- 3. Для чего нужен
- 4. РЕШЕНИЕ УРАВНЕНИЙ МЕТОДОМ ПОДБОРА ПАРАМЕТРОВ EXCELИнструмент «Подбор
- 5. Рассмотрим на примере решение квадратного уравнения х2 +
- 6. 2. Открываем меню инструмента «Подбор параметра». В
- 7. 3. Открываем меню инструмента «Подбор параметра». В
- 8. 4. После нажатия ОК отобразится результат подбора.
- 9. РЕШЕНИЕ ЗАДАЧ ОПТИМИЗАЦИИ В EXCELПодбор параметров («Данные»
- 10. Поиск решения (надстройка Microsoft Excel; «Данные» -
- 11. Для решения простейших задач применяется команда «Подбор
- 12. Условие. Фирма производит несколько сортов йогурта. Условно
- 13. Известные данные (в т.ч. нормы расхода сырья) занесем в таблицу:На основании этих данных составим рабочую таблицу:
- 14. Количество изделий нам пока неизвестно. Это переменные.В
- 15. Активизируем команду «Поиск решения» и вносим параметры.
- 16. После нажатия кнопки «Выполнить» программа выдает свое
- 17. РЕШЕНИЕ ФИНАНСОВЫХ ЗАДАЧ В EXCELЧаще всего для
- 18. Так как процентная ставка не меняется в
- 19. Слайд 19
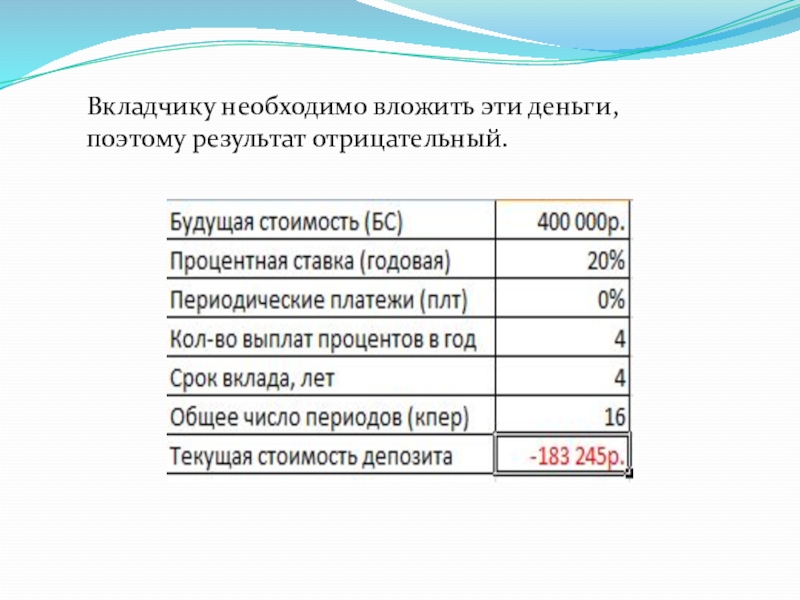
- 20. Вкладчику необходимо вложить эти деньги, поэтому результат отрицательный.
- 21. ПОСТРОЕНИЕ ГРАФИКОВ В EXCEL ПО ДАННЫМ ТАБЛИЦЫРассмотрим
- 22. В нашем случае y=5x-2. В ячейку с первым
- 23. Теперь можно приступать к созданию графика.Выбираем: ВСТАВКА
- 24. Появиться пустая область диаграмм. Нажимаем кнопку ВЫБРАТЬ ДАННЫЕ
- 25. Выберем данные: диапазон ячеек оси абсцисс (х)
- 26. ЗАКЛЮЧЕНИЕExcel – это самое полезное, универсальное и
- 27. СПАСИБО ЗА ВНИМАНИЕ!
Целью моей работы было рассмотреть задачи, решаемых при помощи электронных таблиц. Определить роль Excel в различных сферах деятельности, ведь знание Microsoft Excel стало обязательным требованием для офисных рабочих.
Слайд 1Решение задач при помощи электронных таблиц
Автор: Коротков Павел, 8 класс
Руководитель: Гончарук
А.В.
Слайд 2Целью моей работы было рассмотреть задачи, решаемых при помощи электронных таблиц.
Определить роль Excel в различных сферах деятельности, ведь знание Microsoft Excel стало обязательным требованием для офисных рабочих.
Слайд 3 Для чего нужен EXCEL?
Во первых excel это
самая популярная программа для быстрого и эффективного решения самых разных задач.
Программа способна создавать графики, решать самые различные рода задач: финансовые, экономические, математические, логические, оптимизационные и многие другие.
Например: если получать кредит на закупку товара в банке с более низкой процентной ставкой, а цену товара немного повысить – существенно ли возрастет прибыль при таких условиях?
Программа способна создавать графики, решать самые различные рода задач: финансовые, экономические, математические, логические, оптимизационные и многие другие.
Например: если получать кредит на закупку товара в банке с более низкой процентной ставкой, а цену товара немного повысить – существенно ли возрастет прибыль при таких условиях?
Слайд 4РЕШЕНИЕ УРАВНЕНИЙ МЕТОДОМ ПОДБОРА ПАРАМЕТРОВ EXCEL
Инструмент «Подбор параметра» применяется в ситуации,
когда известен результат, но неизвестны аргументы. Excel подбирает значения до тех пор, пока вычисление не даст нужный итог.
Путь к команде: «Данные» - «Работа с данными» - «Анализ «что-если»» - «Подбор параметра».
Путь к команде: «Данные» - «Работа с данными» - «Анализ «что-если»» - «Подбор параметра».
Слайд 5Рассмотрим на примере решение квадратного уравнения х2 + 3х + 2 =
0. Порядок нахождения корня средствами Excel:
1. Введем в ячейку В2 формулу для нахождения значения функции. В качестве аргумента применим ссылку на ячейку В1.
1. Введем в ячейку В2 формулу для нахождения значения функции. В качестве аргумента применим ссылку на ячейку В1.
Слайд 62. Открываем меню инструмента «Подбор параметра». В графе «Установить в ячейку»
- ссылка на ячейку В2, где находится формула. В поле «Значение» вводим 0. Это то значение, которое нужно получить. В графе «Изменяя значение ячейки» - В1. Здесь должен отобразиться отобранный параметр.
Слайд 73. Открываем меню инструмента «Подбор параметра». В графе «Установить в ячейку»
- ссылка на ячейку В2, где находится формула. В поле «Значение» вводим 0. Это то значение, которое нужно получить. В графе «Изменяя значение ячейки» - В1. Здесь должен отобразиться отобранный параметр.
Слайд 84. После нажатия ОК отобразится результат подбора. Если нужно его сохранить,
вновь нажимаем ОК. В противном случае – «Отмена».
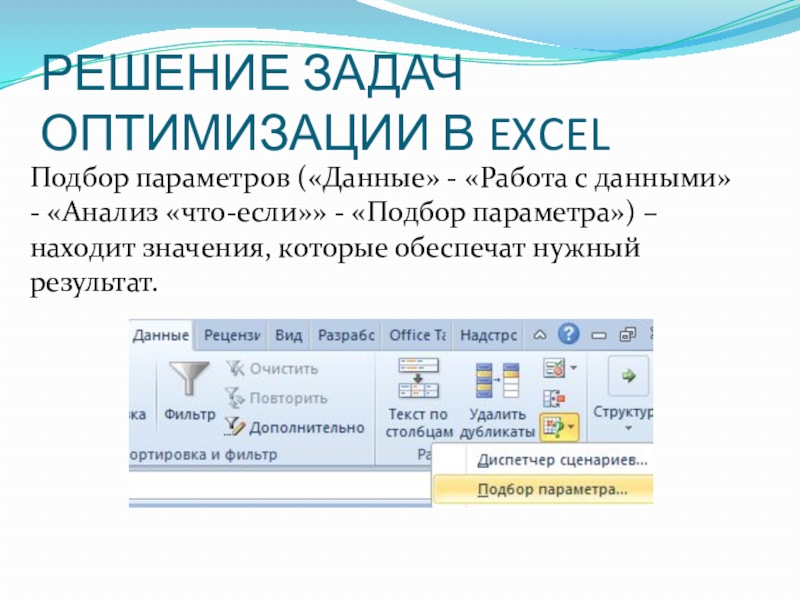
Слайд 9РЕШЕНИЕ ЗАДАЧ ОПТИМИЗАЦИИ В EXCEL
Подбор параметров («Данные» - «Работа с данными»
- «Анализ «что-если»» - «Подбор параметра») – находит значения, которые обеспечат нужный результат.
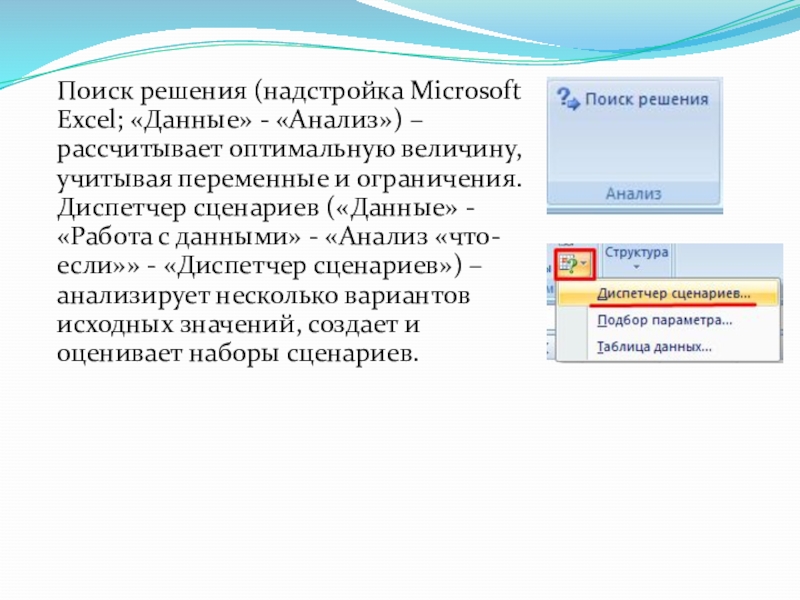
Слайд 10Поиск решения (надстройка Microsoft Excel; «Данные» - «Анализ») – рассчитывает оптимальную
величину, учитывая переменные и ограничения. Диспетчер сценариев («Данные» - «Работа с данными» - «Анализ «что-если»» - «Диспетчер сценариев») – анализирует несколько вариантов исходных значений, создает и оценивает наборы сценариев.
Слайд 11Для решения простейших задач применяется команда «Подбор параметра». Самых сложных –
«Диспетчер сценариев». Рассмотрим пример решения оптимизационной задачи с помощью надстройки «Поиск решения».
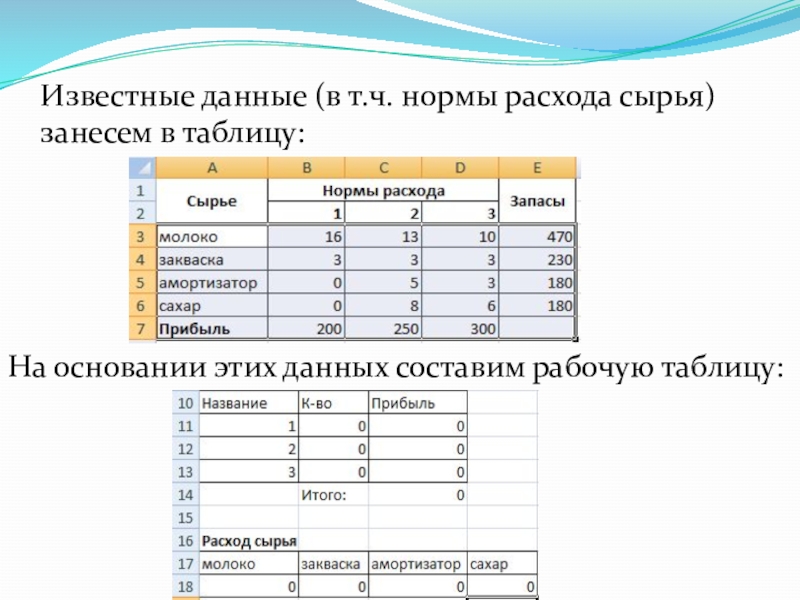
Слайд 12Условие. Фирма производит несколько сортов йогурта. Условно – «1», «2» и
«3». Реализовав 100 баночек йогурта «1», предприятие получает 200 рублей. «2» - 250 рублей. «3» - 300 рублей. Сбыт, налажен, но количество имеющегося сырья ограничено. Нужно найти, какой йогурт и в каком объеме необходимо делать, чтобы получить максимальный доход от продаж.
Слайд 13Известные данные (в т.ч. нормы расхода сырья) занесем в таблицу:
На основании
этих данных составим рабочую таблицу:
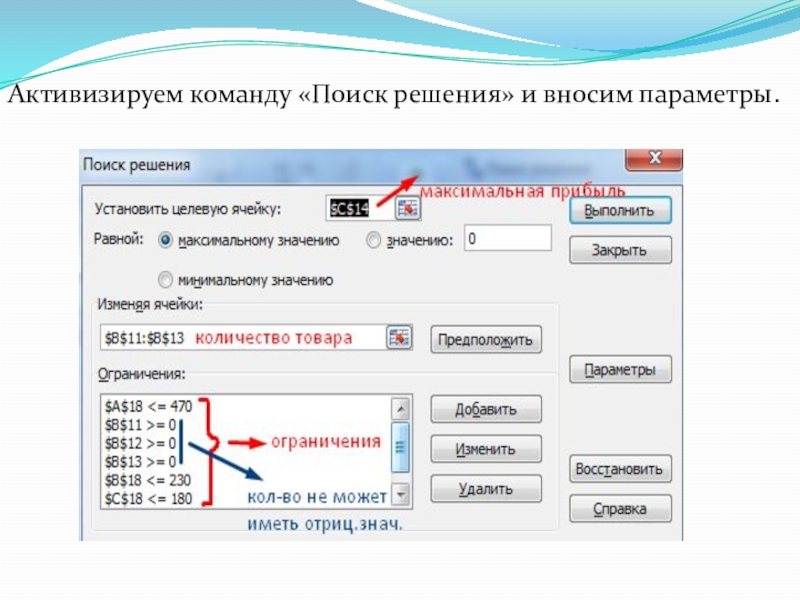
Слайд 14Количество изделий нам пока неизвестно. Это переменные.
В столбец «Прибыль» внесены формулы:
=200*B11, =250*В12, =300*В13.
Расход сырья ограничен (это ограничения). В ячейки внесены формулы: =16*B11+13*B12+10*B13 («молоко»); =3*B11+3*B12+3*B13 («закваска»); =0*B11+5*B12+3*B13 («амортизатор») и =0*B11+8*B12+6*B13 («сахар»). То есть мы норму расхода умножили на количество.
Цель – найти максимально возможную прибыль. Это ячейка С14.
Расход сырья ограничен (это ограничения). В ячейки внесены формулы: =16*B11+13*B12+10*B13 («молоко»); =3*B11+3*B12+3*B13 («закваска»); =0*B11+5*B12+3*B13 («амортизатор») и =0*B11+8*B12+6*B13 («сахар»). То есть мы норму расхода умножили на количество.
Цель – найти максимально возможную прибыль. Это ячейка С14.
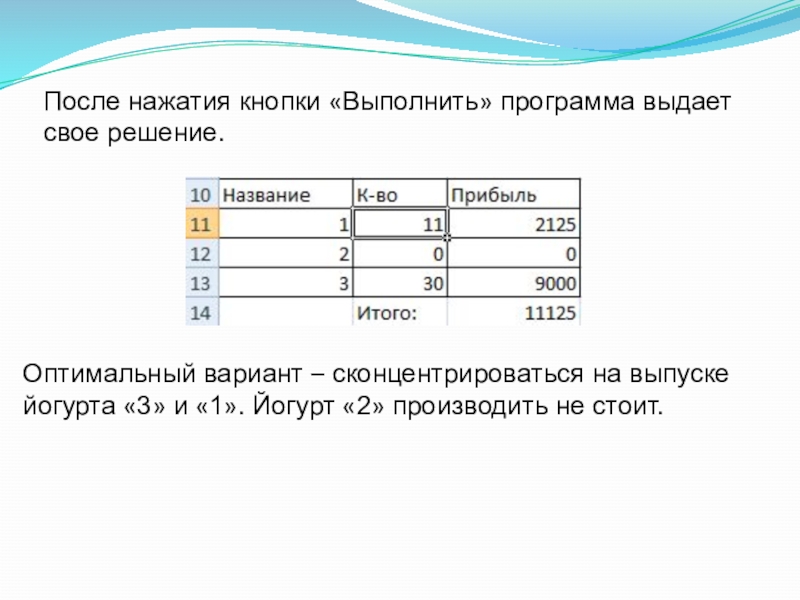
Слайд 16После нажатия кнопки «Выполнить» программа выдает свое решение.
Оптимальный вариант – сконцентрироваться
на выпуске
йогурта «3» и «1». Йогурт «2» производить не стоит.
йогурта «3» и «1». Йогурт «2» производить не стоит.
Слайд 17РЕШЕНИЕ ФИНАНСОВЫХ ЗАДАЧ В EXCEL
Чаще всего для этой цели применяются финансовые
функции. Рассмотрим пример.
Условие. Рассчитать, какую сумму положить на вклад, чтобы через четыре года образовалось 400 000 рублей. Процентная ставка – 20% годовых. Проценты начисляются ежеквартально.
Оформим исходные данные в виде таблицы:
Условие. Рассчитать, какую сумму положить на вклад, чтобы через четыре года образовалось 400 000 рублей. Процентная ставка – 20% годовых. Проценты начисляются ежеквартально.
Оформим исходные данные в виде таблицы:
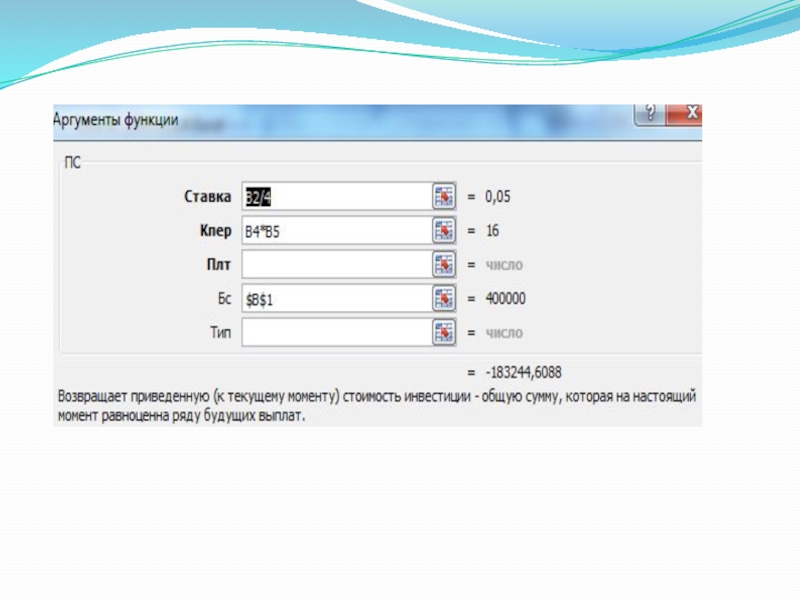
Слайд 18Так как процентная ставка не меняется в течение всего периода, используем
функцию ПС (СТАВКА, КПЕР, ПЛТ, БС, ТИП).
Заполнение аргументов:
Ставка – 20%/4, т.к. проценты начисляются ежеквартально.
Кпер – 4*4 (общий срок вклада * число периодов начисления в год).
Плт – 0. Ничего не пишем, т.к. депозит пополняться не будет.
Тип – 0.
БС – сумма, которую мы хотим получить в конце срока вклада.
Заполнение аргументов:
Ставка – 20%/4, т.к. проценты начисляются ежеквартально.
Кпер – 4*4 (общий срок вклада * число периодов начисления в год).
Плт – 0. Ничего не пишем, т.к. депозит пополняться не будет.
Тип – 0.
БС – сумма, которую мы хотим получить в конце срока вклада.
Слайд 21ПОСТРОЕНИЕ ГРАФИКОВ В EXCEL ПО ДАННЫМ ТАБЛИЦЫ
Рассмотрим пример построения графика линейной
функции: y=5x-2
Графиком линейной функции является прямая, которую можно построить по двум точкам. Создадим табличку
Графиком линейной функции является прямая, которую можно построить по двум точкам. Создадим табличку
Слайд 22В нашем случае y=5x-2. В ячейку с первым значением y введем формулу: =5*D4-2. В другую
ячейку формулу можно ввести аналогично (изменив D4 на D5) или использовать маркер автозаполнения.
В итоге мы получим табличку:
В итоге мы получим табличку:
Слайд 23Теперь можно приступать к созданию графика.
Выбираем: ВСТАВКА — > ТОЧЕЧНАЯ ->
ТОЧЕЧНАЯ С ГЛАДКИМИ КРИВЫМИ И МАРКЕРАМИ (рекомендую использовать именно этот тип диаграммы)
Слайд 25 Выберем данные: диапазон ячеек оси абсцисс (х) и оси ординат (у).
В качестве имени ряда можем ввести саму функцию в кавычках «y=5x-2» или что-то другое. Вот что получилось:
Слайд 26ЗАКЛЮЧЕНИЕ
Excel – это самое полезное, универсальное и многофункциональное программное средство из
пакета Office. Основное назначение Excel – хранение, анализ и визуализация данных, создание отчетов и проведение сложных расчетов.