учитель математики
Мосунова Ольга Анатольевна
- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад на тему Проект-презентация Простые числа
Содержание
- 1. Проект-презентация Простые числа
- 2. План работы : Цель
- 3. Предметом изучения являются простые числа Целью данной
- 4. Для достижения этой цели поставлены задачи :
- 5. Гипотеза Можно указать самое большое простое число
- 6. Определение простого числа. Натуральное число называется
- 7. Теоретическая часть Изучить историю и свойства простых чисел
- 8. Из истории простых чисел Греческий математик
- 9. Первый способ нахождения простых чисел Эратосфен
- 10. Простыми числами занимался и древнегреческий математик Евклид
- 11. Свойства простых чисел Два простых числа,
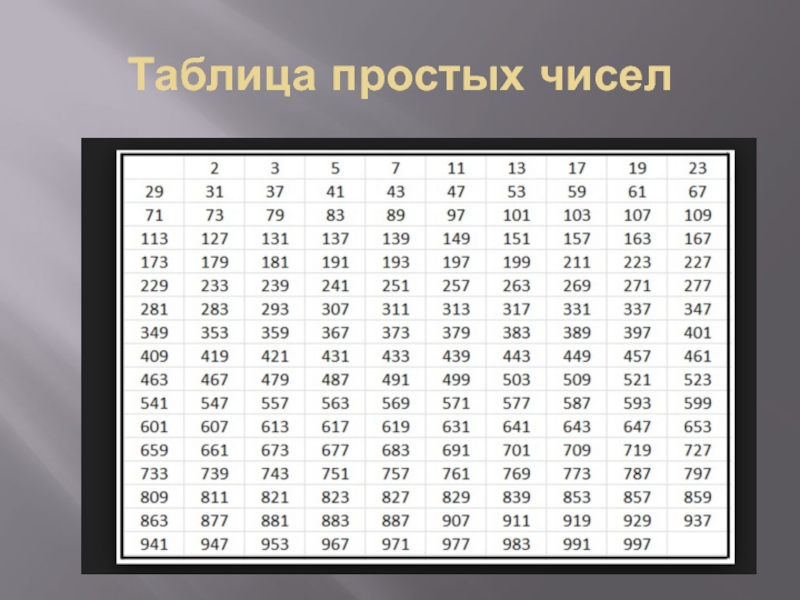
- 12. Таблица простых чисел
- 13. Практическая часть Нахождение простых чисел больше 997 методом «Решето Эратосфена » и составление таблицы
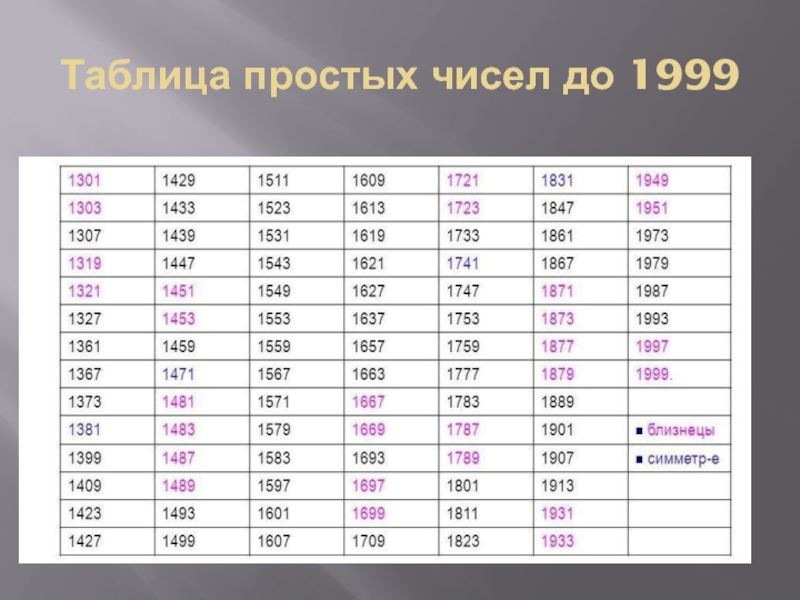
- 14. Таблица простых чисел до 1999
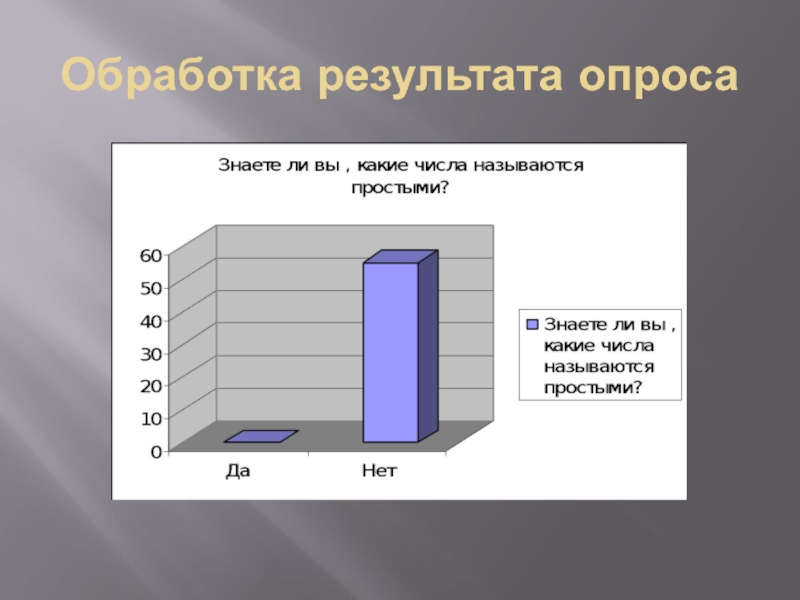
- 15. Обработка результата опроса
- 16. СодержаниеТитульный листЦельГипотезаПланТеорияОбработка результатовИнформационные ресурсыВывод
- 17. Заключение: В своей
План работы : Цель и предмет работы Определение простого числа Теоретическая часть: исторические сведения; свойства простых чисел Практическая часть: нахождение простых чисел, путем освоения метода «Решето Эратосфена», составление таблицы Заключение
Слайд 2
План работы :
Цель и предмет работы
Определение простого числа
Теоретическая
часть: исторические сведения; свойства простых чисел
Практическая часть: нахождение простых чисел, путем освоения метода «Решето Эратосфена», составление таблицы
Заключение
Практическая часть: нахождение простых чисел, путем освоения метода «Решето Эратосфена», составление таблицы
Заключение
Слайд 3Предметом изучения являются простые числа
Целью данной работы является исследование некоторых
свойств и нахождение простых чисел через освоение метода «Решето Эратосфена».
Слайд 4Для достижения этой цели поставлены задачи :
Собрать и изучить материал.
Открыть какие-либо закономерности и свойства в ряду чисел.
Найти простые числа больше числа 997 методом «Решето Эратосфена ».
Слайд 6Определение простого числа.
Натуральное число называется простым , если оно имеет
только два делителя: единицу и само это число. Например: 3 – простое число. Оно нацело делится на 1 и на само себя, т.е. на 3.
Если число имеет более двух делителей, то называется составным.
Если число имеет более двух делителей, то называется составным.
Слайд 8Из истории простых чисел
Греческий математик Эратосфен, живший более чем за
2000 лет до н.э., составил первую таблицу простых чисел, которая получила название «Решето Эратосфена».
А почему решето? Так как греки делали записи на покрытых воском табличках или на натянутом папирусе, а числа не вычёркивали, а выкалывали иглой, то таблица в конце вычислений напоминала решето.
А почему решето? Так как греки делали записи на покрытых воском табличках или на натянутом папирусе, а числа не вычёркивали, а выкалывали иглой, то таблица в конце вычислений напоминала решето.
Слайд 9Первый способ нахождения простых чисел
Эратосфен записывал на дощечке, покрытым воском,
и последовательно прокалывал составные числа. Таким образом, на доске нетронутыми остались лишь простые числа, а составные числа исчезали, как бы просеивались. Оставив нетронутым число 2, он далее прокалывал числа 4,6,8…, т.е. все четные числа, кратные двум. Следующее простое число 3, а все числа, кратные трем, уже составные, поэтому прокалывались все числа через два в третье. Оставив число 5 как простое, прокалываются все числа, кратные 5, т.е. каждое пятое число, и т.д.
Слайд 10Простыми числами занимался и древнегреческий математик Евклид
(IIIв. до н.э.).
В
своей книге «Начала», бывшей на протяжении двух тысяч лет основным учебником математики, доказал, что простых чисел бесконечно много, т.е. за каждым простым числом есть ещё большее простое число.
Слайд 11Свойства простых чисел
Два простых числа, которые отличаются на 2, как
5 и 7, 11 и 13, 17 и 19 и т.д. получили образное название « близнецы ».
Три числа, которые отличаются на 2, называются « тройняшками », 3, 5, 7.
Три числа, которые отличаются на 2, называются « тройняшками », 3, 5, 7.
Слайд 13Практическая часть
Нахождение простых чисел больше 997 методом «Решето Эратосфена »
и составление таблицы
Слайд 16Содержание
Титульный лист
Цель
Гипотеза
План
Теория
Обработка результатов
Информационные ресурсы
Вывод
Слайд 17Заключение:
В своей работе «Простые числа», изучена история,
свойства простых чисел. Отсюда сформулированная гипотеза, что можно указать самое большое простое число, оказалась неверной. Невозможно, указать самое большое простое число, т.к. их бесконечно. Эту теорему доказал древнегреческий математик Евклид III в. до н.э.
В ходе работы были найдены 92 простых числа методом «Решето Эратосфена».
В ходе работы были найдены 92 простых числа методом «Решето Эратосфена».