- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад на тему Проект по математике Удивительные числа
Содержание
- 1. Проект по математике Удивительные числа
- 2. Основополагающий вопрос: В чем секрет необычных чисел?
- 3. Цель работы: как можно больше отыскать удивительных чисел, установить их свойства и закономерности.
- 4. Задачи:1.Рассмотреть основные этапы развития натуральных чисел.2.Выделеть интересные
- 5. План работы:1.История числа.2.Простые числа. Решето Эратосфена.3.Числа-близнецы.4.Фигурные числа.5.Многоугольные числа.6.Дружественные числа.7.Совершенные числа.8.Компанейские числа.9.Число Шахиризады.10. Заключение.
- 6. Предмет исследования: натуральные удивительные числа и их свойства.
- 7. Метод исследования:основным методом исследования видов чисел являются изучение и обработка литературных источников, систематизация данных.
- 8. Возникновение чисел в нашей жизни не
- 9. О числе.Число является одним из основных
- 10. Простые числа. Решето Эратосфена. Каждое натуральное число,
- 11. Слайд 11
- 12. Числа близнецы.Два простых числа, которые отличаются на
- 13. Числа близнецы.
- 14. Фигурные числа.Фигурные числа — общее название чисел,
- 15. Фигурные числа.
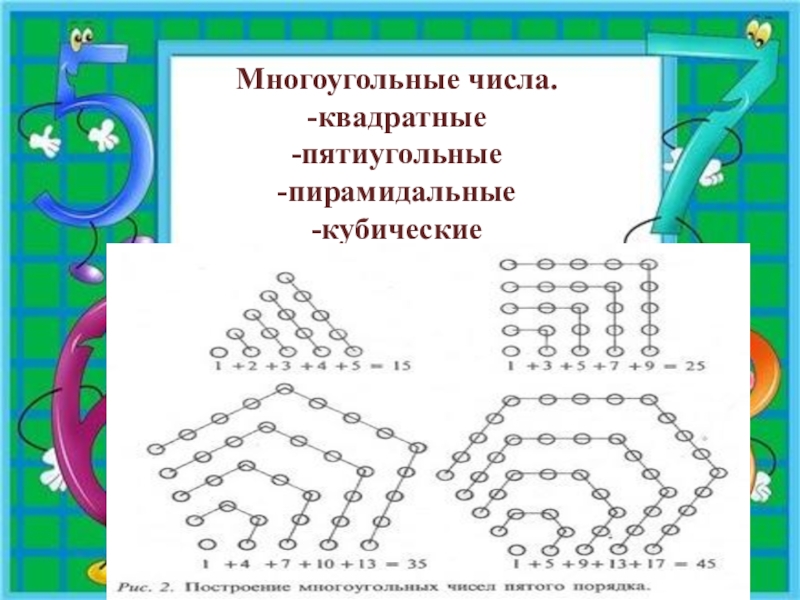
- 16. Многоугольные числа. -квадратные -пятиугольные -пирамидальные -кубические
- 17. Дружественные числа. Дружественные числа – это два натуральных
- 18. Совершенные числа.Иногда частным случаем дружественных чисел считаются
- 19. Компанейские числа.Понятие совершенных и дружественных чисел часто
- 20. Число Шахиризады.Число Шахиризды- число 1001, которое фигурирует
- 21. Число Шахиризады.
- 22. Заключение.Среди всех интересных натуральных чисел, издавна изучаемых
- 23. Заключение.Причем нередко одно и тоже открытие происходило
- 24. Спасибо за внимание!
Основополагающий вопрос: В чем секрет необычных чисел?
Слайд 1Проект
на тему:
«Удивительные числа».
Автор: Валерия Вереновская, ученица 6б класса
Руководитель: Н.Т.Маляренко
Слайд 3 Цель работы: как можно больше отыскать удивительных чисел, установить их свойства
и закономерности.
Слайд 4Задачи:
1.Рассмотреть основные этапы развития натуральных чисел.
2.Выделеть интересные виды удивительных натуральных чисел:
простые, числа-близнецы, фигурные, совершенные, дружественные и другие.
3.Установить целый ряд свойств, законов и закономерностей этих чисел.
4.Раскрыть таинственную магию и суеверие о некоторых числах.
3.Установить целый ряд свойств, законов и закономерностей этих чисел.
4.Раскрыть таинственную магию и суеверие о некоторых числах.
Слайд 5План работы:
1.История числа.
2.Простые числа. Решето Эратосфена.
3.Числа-близнецы.
4.Фигурные числа.
5.Многоугольные числа.
6.Дружественные числа.
7.Совершенные числа.
8.Компанейские числа.
9.Число
Шахиризады.
10. Заключение.
10. Заключение.
Слайд 7Метод исследования:
основным методом исследования видов чисел являются изучение и обработка литературных
источников, систематизация данных.
Слайд 8 Возникновение чисел в нашей жизни не случайность. Невозможно представить себе общение
без использования чисел. История чисел увлекательна и загадочна. Человечеству удалось установить целый ряд законов и закономерностей мира чисел , разгадать кое-какие тайны и использовать свои открытия в повседневной жизни. Без замечательной науки о числах- математики- немыслимо сегодня ни прошлое, ни будущее. А сколько всего неразгаданного!
Слайд 9 О числе.
Число является одним из основных понятий математики. Понятие числа
развивалось в тесной связи с изучением величин; эта связь сохранилась и теперь.
Существует большое количество определений понятию Число. О первых числах начал рассуждал Пифагор. Пифагору принадлежит высказывание «Всё прекрасно брагодаря числу». По его учению число 2 означало гармонию, 5- цвет, 6- холод,7- разум ,здоровье, 8- любовь, дружбу. А число 10 называли Священной четверицей, так как 10= 1+2+3+4. Оно считалось священным числом и олицетворяла всю Вселенную.
Существует большое количество определений понятию Число. О первых числах начал рассуждал Пифагор. Пифагору принадлежит высказывание «Всё прекрасно брагодаря числу». По его учению число 2 означало гармонию, 5- цвет, 6- холод,7- разум ,здоровье, 8- любовь, дружбу. А число 10 называли Священной четверицей, так как 10= 1+2+3+4. Оно считалось священным числом и олицетворяла всю Вселенную.
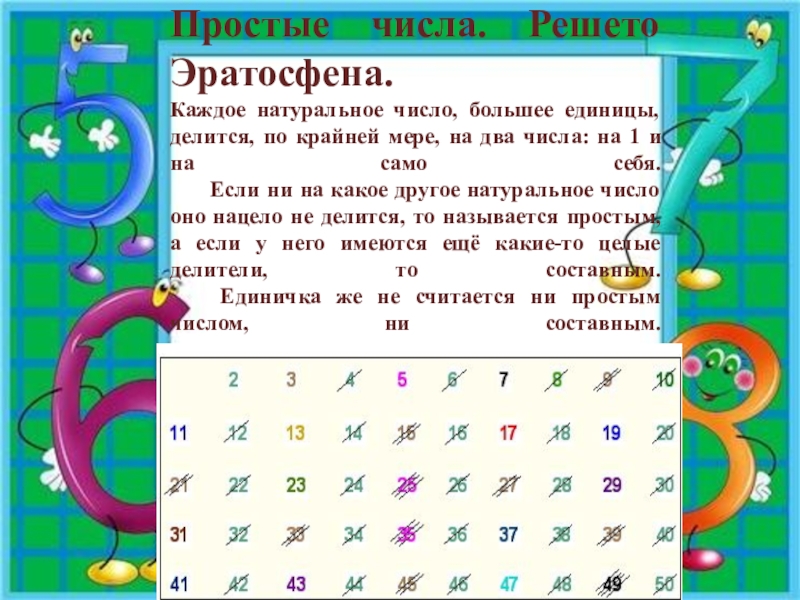
Слайд 10Простые числа. Решето Эратосфена. Каждое натуральное число, большее единицы, делится, по крайней
мере, на два числа: на 1 и на само себя.
Если ни на какое другое натуральное число оно нацело не делится, то называется простым, а если у него имеются ещё какие-то целые делители, то составным.
Единичка же не считается ни простым числом, ни составным.
Слайд 11
«Просеивание чисел»
Выпишем несколько подряд идущих чисел, начиная с
2.
Двойку отберём в свою коллекцию, а остальные числа, кратные 2, зачеркнем. Ближайшим не зачёркнутым числом будет 3. Возьмём в коллекцию и его, а все остальные числа, кратные 3, зачеркнем. При этом окажется, что некоторые числа уже были вычеркнуты раньше, как, например, 6, 12 и др. Следующее наименьшее не зачёркнутое число – это 5. Берем пятерку, а остальные числа, кратные 5,зачеркиваем.
Повторяя эту процедуру снова и снова, в конце концов добьемся того, что не зачеркнутыми останутся одни лишь простые числа – они словно просеялись сквозь решето.
Поэтому такой способ и получил название "решето Эратосфена".
Двойку отберём в свою коллекцию, а остальные числа, кратные 2, зачеркнем. Ближайшим не зачёркнутым числом будет 3. Возьмём в коллекцию и его, а все остальные числа, кратные 3, зачеркнем. При этом окажется, что некоторые числа уже были вычеркнуты раньше, как, например, 6, 12 и др. Следующее наименьшее не зачёркнутое число – это 5. Берем пятерку, а остальные числа, кратные 5,зачеркиваем.
Повторяя эту процедуру снова и снова, в конце концов добьемся того, что не зачеркнутыми останутся одни лишь простые числа – они словно просеялись сквозь решето.
Поэтому такой способ и получил название "решето Эратосфена".
Слайд 12Числа близнецы.
Два простых числа, которые отличаются на 2, как 5 и
7, 11 и 13, 17 и 19, получили название числа близнецы. В натуральном ряду имеется даже тройня- это числа 3,5,7. Ну а сколько всего существует близнецов- современной науке не известно.
В пределах первой сотни близнецы- это следующие пары чисел (3,5), (5,7), (11,13), (17,19), (29,31), (41,43), (59,61), (71,73). По мере удаления от нуля близнецов становится всё меньше и меньше. Близнецы могут собираться в скопления, образуя четверки, например: (5,7,11,13) или (11,13,17,19).как много таких скоплений- тоже пока неизвестно.
В пределах первой сотни близнецы- это следующие пары чисел (3,5), (5,7), (11,13), (17,19), (29,31), (41,43), (59,61), (71,73). По мере удаления от нуля близнецов становится всё меньше и меньше. Близнецы могут собираться в скопления, образуя четверки, например: (5,7,11,13) или (11,13,17,19).как много таких скоплений- тоже пока неизвестно.
Слайд 14
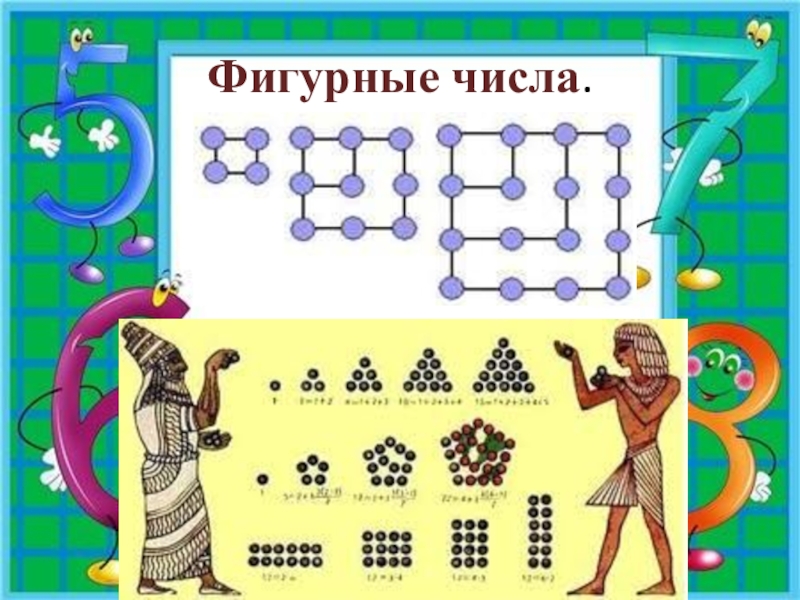
Фигурные числа.
Фигурные числа — общее название чисел, связанных с той или иной
геометрической фигурой.
Давным-давно, помогая себе при счете камушками, люди обращали внимание на правильные фигуры, которые можно выложить из камушков.
Можно просто класть камушки в ряд: один, два, три. Если класть их в два ряда, чтобы получались прямоугольники, то получаются все четные числа.
Можно выкладывать камни в три ряда: получатся числа, делящиеся на три.
Давным-давно, помогая себе при счете камушками, люди обращали внимание на правильные фигуры, которые можно выложить из камушков.
Можно просто класть камушки в ряд: один, два, три. Если класть их в два ряда, чтобы получались прямоугольники, то получаются все четные числа.
Можно выкладывать камни в три ряда: получатся числа, делящиеся на три.
Слайд 17Дружественные числа.
Дружественные числа – это два натуральных числа, для которых сумма
всех делителей первого числа (кроме него самого) равна второму числу и сумма всех делителей второго числа (кроме него самого) равна первому числу.
История дружественных чисел теряется в глубине веков. Эти удивительные числа были открыты последователями Пифагора. Правда пифагорейцы знали только одну пару дружественных чисел – 220 и 284. Проверим эту пару чисел на свойство дружественных чисел:
1 + 2 + 4 + 5 + 10 + 11 + 20 + 22 + 44 + 55 + 110 = 284
1 + 2 + 4 + 71 + 142 = 220
История дружественных чисел теряется в глубине веков. Эти удивительные числа были открыты последователями Пифагора. Правда пифагорейцы знали только одну пару дружественных чисел – 220 и 284. Проверим эту пару чисел на свойство дружественных чисел:
1 + 2 + 4 + 5 + 10 + 11 + 20 + 22 + 44 + 55 + 110 = 284
1 + 2 + 4 + 71 + 142 = 220
Слайд 18Совершенные числа.
Иногда частным случаем дружественных чисел считаются совершенные числа: каждое совершенное
число дружественно себе. Никомах Герасский, знаменитый философ и математик, писал: «Совершенные числа красивы».
Но известно, что совершенные вещи редки и немногочисленны, безобразные встречаются в изобилии. Избыточными и недостаточными являются почти все числа, в то время как совершенных чисел немного" Но, сколько их, Никомах, живший в первом столетии нашей эры не знал.
Совершенным называется число, равное сумме всех своих делителей (включая 1, но исключая само число).
Первым прекрасным совершенным числом, о котором знали математики Древней Греции, было число "6". На шестом месте на званном пиру возлежал самый уважаемый, самый почетный гость. В библейских преданиях утверждается, что мир был создан в шесть дней, ведь более совершенного числа, среди совершенных чисел, чем "6", нет, поскольку оно первое среди них.
Рассмотрим число 6. Число имеет делители 1, 2, 3 и само число 6. Если сложить делители, отличные от самого числа 1 + 2 + 3 то мы получим 6. Значит, число 6 дружественно самому себе и является первым совершенным числом.
Но известно, что совершенные вещи редки и немногочисленны, безобразные встречаются в изобилии. Избыточными и недостаточными являются почти все числа, в то время как совершенных чисел немного" Но, сколько их, Никомах, живший в первом столетии нашей эры не знал.
Совершенным называется число, равное сумме всех своих делителей (включая 1, но исключая само число).
Первым прекрасным совершенным числом, о котором знали математики Древней Греции, было число "6". На шестом месте на званном пиру возлежал самый уважаемый, самый почетный гость. В библейских преданиях утверждается, что мир был создан в шесть дней, ведь более совершенного числа, среди совершенных чисел, чем "6", нет, поскольку оно первое среди них.
Рассмотрим число 6. Число имеет делители 1, 2, 3 и само число 6. Если сложить делители, отличные от самого числа 1 + 2 + 3 то мы получим 6. Значит, число 6 дружественно самому себе и является первым совершенным числом.
Слайд 19Компанейские числа.
Понятие совершенных и дружественных чисел часто упоминается в литературе по
занимательной математике. Однако почему- то мало говорится о том, что числа могут дружить и компаниями. Понятие компанейских чисел хорошо раскрывается в англоязычных источниках.
Компанейскими называется такая группа из k чисел, в которых сумма собственных делителей первого числа равна второму, сумма собственных делителей второго- третьему и т.д. А первое число равно сумме собственных делителей k- го числа.
Есть компании по 4,5,6,8,9 и даже 28 участников, а вот по три не найдено. Пример пятёрки, пока единственно известной: 12496,14288,15472,14536,14264.
-- 666. Это означает, что 666- это 36-е треугольное число.
Компанейскими называется такая группа из k чисел, в которых сумма собственных делителей первого числа равна второму, сумма собственных делителей второго- третьему и т.д. А первое число равно сумме собственных делителей k- го числа.
Есть компании по 4,5,6,8,9 и даже 28 участников, а вот по три не найдено. Пример пятёрки, пока единственно известной: 12496,14288,15472,14536,14264.
-- 666. Это означает, что 666- это 36-е треугольное число.
Слайд 20Число Шахиризады.
Число Шахиризды- число 1001, которое фигурирует в заглавии бессмертных сказок
«Тысяча и одна ночь». С точки зрения математики число 1001 обладает целым рядом интереснейших свойств: это самое маленькое натуральное четырёхзначное число, которое можно представить в виде суммы кубов двух натуральных чисел: 1001=10³+1³; число 1001 стоит из 77 злополучных чертовых дюжин (1001=13? 77); или из 91 числа 11, или из 143 семёрок; далее, если будем считать, что год равняется 52 неделям, то 1001- количество ночей в течением1+1+ года или по другому: 1001=52?7+26.7+13?7. В числе Шахиризады литература переплетается с математикой
Слайд 22Заключение.
Среди всех интересных натуральных чисел, издавна изучаемых математиками, особое место занимают
совершенные и близко связанные с ними дружественные числа.
Из огромного многообразия натуральных чисел ученые выделили дружественные и совершенные числа, обладающие рядом очень интересных свойств.
Анализируя научно- популярную литературу о совершенных и дружественных числах, можно убедиться, что формулы общего вида для нахождения всех пар дружественных, совершенных чисел не существует. Вопрос о существовании: бесконечности множества четных совершенных чисел, нечетного совершенного числа, четно- нечетной пары дружественных чисел и взаимно простых дружественных чисел открыт до сих пор.
Из огромного многообразия натуральных чисел ученые выделили дружественные и совершенные числа, обладающие рядом очень интересных свойств.
Анализируя научно- популярную литературу о совершенных и дружественных числах, можно убедиться, что формулы общего вида для нахождения всех пар дружественных, совершенных чисел не существует. Вопрос о существовании: бесконечности множества четных совершенных чисел, нечетного совершенного числа, четно- нечетной пары дружественных чисел и взаимно простых дружественных чисел открыт до сих пор.
Слайд 23Заключение.
Причем нередко одно и тоже открытие происходило в разных точках земного
шара, довольно часто повторялось несколько раз, совершенствовалось, а позже распространялось и становилось достоянием всех народов. Математика невольно связывает единой нитью народы мира. Она заставляет их сотрудничать и общаться между собой.
Мир полон тайн и загадок. Но разгадать их могут только пытливые.
Современная наука встречаться с величинами такой сложной природы. Что для их изучения приходиться изобретать все новые виды чисел. И мне бы хотелось продолжить изучение чисел, ведь я только знаю натуральные числа и целые числа
Мир полон тайн и загадок. Но разгадать их могут только пытливые.
Современная наука встречаться с величинами такой сложной природы. Что для их изучения приходиться изобретать все новые виды чисел. И мне бы хотелось продолжить изучение чисел, ведь я только знаю натуральные числа и целые числа