- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад на тему Проект История развития геометрии.
Содержание
- 1. Проект История развития геометрии.
- 2. Цели проекта:1. Узнать : а) значение слова
- 3. ЗНАЧЕНИЕ СЛОВА
- 4. Как возникла геометрия?
- 5. Слайд 5
- 6. Возникновение геометрии в Египте.Пирамиды – а они
- 7. Возникновение и развитие геометрии
- 8. Как возникла геометрия? Для первобытных людей важную
- 9. Муза геометрииАвтор (мастер):
- 10. Слайд 10
- 11. Пифагор Самосский
- 12. АрхимедАрхиме́д — древнегреческий математик, физик и инженер
- 13. Происхождение цилиндра А когда стали строить здания
- 14. Геометрия для обороныПод руководством Архимеда Сиракузцы
- 15. Винт Архимеда.Главную часть мясорубки – винт, который
- 16. Геометрические узорыУчёные, изучающие древние постройки, нашли много
- 17. Древний ЕгипетДревний Египет считается первым государством, оставившим
- 18. Как возникла геометрияГеометрия возникла в результате практической
- 19. Слайд 19
- 20. Что такое геометрия?
- 21. Планиметрия – раздел геометрии, изучающий свойства фигур
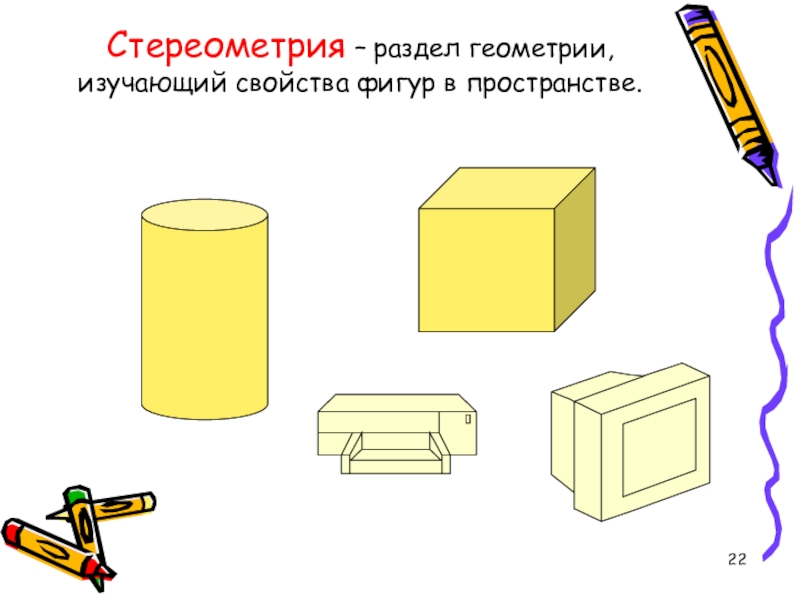
- 22. Стереометрия – раздел геометрии, изучающий свойства фигур в пространстве.
- 23. Геометрия , по свидетельству греческих историков, была
- 24. Великий ученый
- 25. Фалес Милетский Oснователь милетской школы, один из легендарных
- 26. Фалес решил следующие задачи.Предложил способ определения расстояния
- 27. Задача
- 28. «Начала» ЕвклидаЦентральное место среди античных трудов по
- 29. Сочинение Евклида «Начала» почти 2000 лет служило
- 30. Слайд 30
- 31. Средние векаСредние века немного дали геометрии, и
- 32. Геометрия Лобачевского В 1826 году
- 33. Никола́й Ива́нович Лобаче́вский (20 ноября (1 декабря)
- 34. Юбилейные медали
- 35. Геометрические фигуры вокруг нас
- 36. Расчеты современных ученых показывают, что все, связанное
- 37. Это мы- 6 «В»
Цели проекта:1. Узнать : а) значение слова геометрия; б) для чего нужна была геометрия древним людям?
Слайд 1Проект учащихся
6В класса «История
развития геометрии»
ФГОС. Внеурочная деятельность.
МБУ гимназия №35
г.о.Тольятти
Слайд 2Цели проекта:
1. Узнать : а) значение слова геометрия;
б) для чего нужна была геометрия
древним людям?
в) в каком государстве зародилась
геометрия?
г) для чего нужна геометрия
современным людям?
2. Основоположники геометрии.
3. Сделать выводы.
4. Создать презентацию, как результат совместной
деятельности класса над проектом.
древним людям?
в) в каком государстве зародилась
геометрия?
г) для чего нужна геометрия
современным людям?
2. Основоположники геометрии.
3. Сделать выводы.
4. Создать презентацию, как результат совместной
деятельности класса над проектом.
Слайд 3 ЗНАЧЕНИЕ СЛОВА «ГЕОМЕТРИЯ»
Геометрия - одна из
самых древних наук, ее возраст исчисляется тысячелетиями. Геометрия (греч. geometria, от geо - Земля и metreo - мерю), раздел математики, изучающий пространственные отношения и формы, а также другие отношений и формы, сходные с пространственными по своей структуре.
В геометрии много формул, фигур, теорем, задач, аксиом. Они вечны, так как на них запечатлены великие идеи, не проходящие идеи.
В геометрии много формул, фигур, теорем, задач, аксиом. Они вечны, так как на них запечатлены великие идеи, не проходящие идеи.
Слайд 4Как возникла геометрия?
Геометрия возникла и развивалась в связи с
потребностями практической деятельности
человека. С древних времён люди сталкивались
с необходимостью находить расстояния между
предметами, определять размеры участков
земли, ориентироваться по расположению звёзд
на небе и т. п.
О зарождении геометрии в Древнем Египте
около 2000 лет до н. э. древнегреческий историк
Геродот писал :
" Сезострус, египетский фараон, разделил
землю, дав каждому египтянину участок по
жребию, и взимал соответствующим образом
налог с каждого участка. Случилось , что Нил заливал тот или иной
участок, тогда пострадавший обращался к царю ,а царь посылал
землемеров, чтобы установить , на сколько уменьшился
участок, и соответствующим образом уменьшить налог. Так
возникла геометрия в Египте, а оттуда перешла в Грецию".
потребностями практической деятельности
человека. С древних времён люди сталкивались
с необходимостью находить расстояния между
предметами, определять размеры участков
земли, ориентироваться по расположению звёзд
на небе и т. п.
О зарождении геометрии в Древнем Египте
около 2000 лет до н. э. древнегреческий историк
Геродот писал :
" Сезострус, египетский фараон, разделил
землю, дав каждому египтянину участок по
жребию, и взимал соответствующим образом
налог с каждого участка. Случилось , что Нил заливал тот или иной
участок, тогда пострадавший обращался к царю ,а царь посылал
землемеров, чтобы установить , на сколько уменьшился
участок, и соответствующим образом уменьшить налог. Так
возникла геометрия в Египте, а оттуда перешла в Грецию".
Слайд 6Возникновение геометрии в Египте.
Пирамиды – а они построены более 5 тыс.
лет назад – состоят из каменных блоков весом 15 тонн, и эти «кирпичики» так подогнаны друг к другу, что не возможно между ними протиснуть и почтовую открытку. А при строительстве использовали лишь простейшие механизмы – рычаги и катки.
«Все боится времени, но само время боится пирамид».
В Вавилоне при раскопках ученые обнаружили остатки каменных стен, высотой в несколько десятков метров, а высота Вавилонской башни достигает 82 метра.
Без математических знаний все эти сооружения невозможно было бы построить. И все же математические знания египтян и вавилонян были разрозненные и представляли собой свод правил, проверенных практикой, поэтому правила надо было зазубривать, не понимая, почему надо применять то, а не другое.
Почти все великие ученые древности и средних веков были выдающимися геометрами. Девиз древней школы был: "Не знающие геометрии не допускаются!"
«Все боится времени, но само время боится пирамид».
В Вавилоне при раскопках ученые обнаружили остатки каменных стен, высотой в несколько десятков метров, а высота Вавилонской башни достигает 82 метра.
Без математических знаний все эти сооружения невозможно было бы построить. И все же математические знания египтян и вавилонян были разрозненные и представляли собой свод правил, проверенных практикой, поэтому правила надо было зазубривать, не понимая, почему надо применять то, а не другое.
Почти все великие ученые древности и средних веков были выдающимися геометрами. Девиз древней школы был: "Не знающие геометрии не допускаются!"
Слайд 8Как возникла геометрия?
Для первобытных людей важную роль играла форма окружавших
их предметов.
Эти формы они использовали, изготовляя каменные орудия.
Уже 200 тысяч лет тому назад были изготовлены орудия сравнительно правильной геометрической формы
Давно уже люди заметили, что глина не пропускает воду. Из неё лепили они горшки и другую посуду. До нас дошли обломки древней глиняной посуды, по которым можно видеть, как лучше и лучше овладевал человек различными геометрическими формами. И вот настал день, когда был изготовлен первый гончарный круг. На нём уже можно было придавать посуде округлую форму.
Эти формы они использовали, изготовляя каменные орудия.
Уже 200 тысяч лет тому назад были изготовлены орудия сравнительно правильной геометрической формы
Давно уже люди заметили, что глина не пропускает воду. Из неё лепили они горшки и другую посуду. До нас дошли обломки древней глиняной посуды, по которым можно видеть, как лучше и лучше овладевал человек различными геометрическими формами. И вот настал день, когда был изготовлен первый гончарный круг. На нём уже можно было придавать посуде округлую форму.
Слайд 9 Муза геометрии
Автор (мастер): - Гольциус
Хендрик
Место создания: - Нидерланды
Материалы техники: бумага; резец на меди
Период создания: 1592 г.
Местонахождение: Государственное учреждение культуры Ярославской области "Рыбинский государственный историко-архитектурный и художественный музей-заповедник"
Изображена на фоне скал в виде молодой женщины в антикизированых одеждах. Эрато сидит на возвышении, правой рукой облокотившись на большой камень. Поворот фигуры в 3/4 вправо. В левой руке муза держит шар, в правой - циркуль. Слева у ее ног лежат две книги и угломерная линейка.
Слайд 11 Пифагор Самосский
Пифагор Самосский,
(570—490 гг. до н. э.)
Древнегреческий философ и математик
Создатель религиозно-философской школы пифагорейцев
«Его философия распространилась, вся Эллада стала восхищаться им, и лучшие и мудрейшие мужи приезжали к нему на Самосс, желая слушать его учение. Сограждане, однако, принуждали его участвовать во всех посольствах и общественных делах. Пифагор чувствовал, как тяжело, подчиняясь законам отечества, одновременно заниматься философией, и видел, что все прежние философы прожили жизнь на чужбине. Обдумав всё это, отойдя от общественных дел и, как говорят некоторые, считая недостаточной невысокую оценку самоссцами его учения, он уехал в Италию,
считая своим отечеством страну, где больше
способных к обучению людей.»
Древнегреческий философ и математик
Создатель религиозно-философской школы пифагорейцев
«Его философия распространилась, вся Эллада стала восхищаться им, и лучшие и мудрейшие мужи приезжали к нему на Самосс, желая слушать его учение. Сограждане, однако, принуждали его участвовать во всех посольствах и общественных делах. Пифагор чувствовал, как тяжело, подчиняясь законам отечества, одновременно заниматься философией, и видел, что все прежние философы прожили жизнь на чужбине. Обдумав всё это, отойдя от общественных дел и, как говорят некоторые, считая недостаточной невысокую оценку самоссцами его учения, он уехал в Италию,
считая своим отечеством страну, где больше
способных к обучению людей.»
Слайд 12Архимед
Архиме́д — древнегреческий математик, физик и инженер из Сиракуз. Сделал множество
открытий в геометрии. Сведения о жизни Архимеда оставили нам Полибий, Тит Ливий, Цицерон, Плутарх, Витрувий и другие. Почти все они жили на много лет позже описываемых событий, и достоверность этих сведений оценить трудно.
Архимед родился в Сиракузах, греческой колонии на острове Сицилия. Отцом Архимеда был математик и астроном Фидий, состоявший, как утверждает Плутарх, в близком родстве с Гиероном II, тираном Сиракуз. Отец привил сыну с детства любовь к математике, механике и астрономии. Для обучения Архимед
отправился в Александрию
Египетскую — научный и
культурный город.
Архимед родился в Сиракузах, греческой колонии на острове Сицилия. Отцом Архимеда был математик и астроном Фидий, состоявший, как утверждает Плутарх, в близком родстве с Гиероном II, тираном Сиракуз. Отец привил сыну с детства любовь к математике, механике и астрономии. Для обучения Архимед
отправился в Александрию
Египетскую — научный и
культурный город.
Слайд 13Происхождение цилиндра
А когда стали строить здания из камня, пришлось перетаскивать
тяжёлые каменные глыбы. Для этого издавна применяли катки. И было замечено, что перекатка тяжёлого камня становилось легче, если для катка взято прямое дерево и от него отрезан кусок с почти одинаковой толщиной в начале и конце. Так люди познакомились с одной из важнейших фигур – цилиндром.
Скалками цилиндрической формы пользовались и женщины,
раскатывая бельё после стирки.
Скалками цилиндрической формы пользовались и женщины,
раскатывая бельё после стирки.
Слайд 14Геометрия для обороны
Под руководством Архимеда Сиракузцы построили много военных машин
для метания тяжёлых камней и брёвен.
Кроме того, пользуясь своими знаниями по геометрии, Архимед, как говорит предание, построил громадные зеркала и с их помощью сжёг римские корабли.
Кроме того, пользуясь своими знаниями по геометрии, Архимед, как говорит предание, построил громадные зеркала и с их помощью сжёг римские корабли.
Слайд 15Винт Архимеда.
Главную часть мясорубки – винт, который вертится внутри трубки и
толкает мясо к ножам, - изобрёл Архимед две с лишним тысячи лет назад. Он придумал его, конечно, не для мясорубки, а для насосов, которыми качали воду на поля.
Слайд 16Геометрические узоры
Учёные, изучающие древние постройки, нашли много рисунков, украшавших их полы
и стены. Полы дворцов часто складывали из мраморных плит различной формы или из дощечек, сделанных из ценных пород дерева. Сложенные из дощечек полы называют паркетными.
Слайд 17Древний Египет
Древний Египет считается первым государством, оставившим самые ранние математические тексты.
Древние греки, достижения которых лежат в основе современной науки, считали себя учениками египтян. Геродот писал: «Египетские жрецы говорили, что царь разделил землю между всеми египтянами, дав каждому по равному прямоугольному участку; из этого он создал себе доходы, приказав ежегодно вносить налог. Если же река отнимала что-нибудь, то царь посылал людей, которые должны измерить участок и уменьшить налог».
Первой книгой, содержащей геометрические задачи, считается папирус Райнда (в некоторых источниках Г.Ринла), который датируется ХХ веком до нашей эры.
Первой книгой, содержащей геометрические задачи, считается папирус Райнда (в некоторых источниках Г.Ринла), который датируется ХХ веком до нашей эры.
Слайд 18Как возникла геометрия
Геометрия возникла в результате практической деятельности людей: нужно было
сооружать жилища, храмы, проводить дороги, оросительные каналы, устанавливать границы земельных участков и определять их размеры. Важную роль играли и эстетические потребности людей: желание украсить свои жилища и одежду,
рисовать картины
окружающей жизни.
рисовать картины
окружающей жизни.
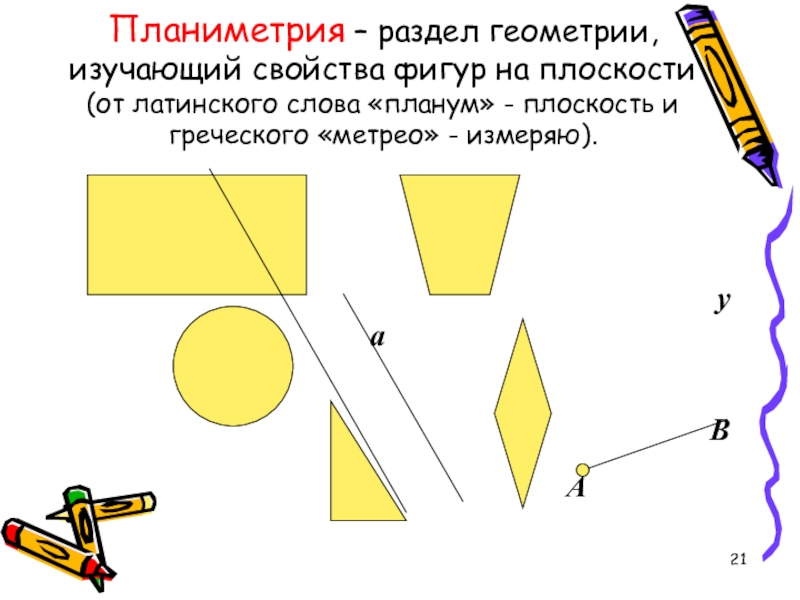
Слайд 21Планиметрия – раздел геометрии, изучающий свойства фигур на плоскости (от латинского
слова «планум» - плоскость и греческого «метрео» - измеряю).
а
А
В
у
Слайд 23Геометрия , по свидетельству греческих историков, была перенесена в Грецию из
Египта в 7 в. до н. э. Здесь на протяжении нескольких поколений она складывалась в стройную систему. Процесс этот происходил путём накопления новых геометрических знаний, выяснения связей между разными геометрическими фактами, выработки приёмов доказательств и, наконец, формирования понятий о фигуре, о геометрическом предложении и о доказательстве. Этот процесс привёл, наконец, к качественному скачку.
Геометрия превратилась в самостоятельную математическую науку: появились систематические её изложения, где её предложения последовательно доказывались.
Геометрия превратилась в самостоятельную математическую науку: появились систематические её изложения, где её предложения последовательно доказывались.
Слайд 24 Великий ученый Фалес Милетский
основал одну из прекраснейших наук – геометрию.
Фалес Милетский имел титул одного из семи мудрецов Греции, он был поистине первым философом, первым математиком, астрономом и вообще первым по всем наукам в Греции.
Фалес Милетский имел титул одного из семи мудрецов Греции, он был поистине первым философом, первым математиком, астрономом и вообще первым по всем наукам в Греции.
VI век до нашей эры
Слайд 25Фалес Милетский
Oснователь милетской школы, один из легендарных "семи мудрецов". Происходил из
аристократического рода, был связан с храмом Аполлона Дидимского, патрона морской колонизации. Имя Фалеса уже в V в. стало нарицательным для мудреца. Считается, что Фалес ввел в употребление новое созвездие - Малую Медведицу.
Фалеса называют одним из первых греческих мыслителей, кто понял важность астрологии как науки. В историю вошло "затмение Фалеса " 28 мая 585 г. до н.э., предсказанное им за 6 лет до события (некоторые ученые считают это легендой, доказывая, что уровень развития науки во времена Фалеса еще не позволял предсказывать затмения). В честь Фалеса названа малая планета
6001 Thales.
Фалеса называют одним из первых греческих мыслителей, кто понял важность астрологии как науки. В историю вошло "затмение Фалеса " 28 мая 585 г. до н.э., предсказанное им за 6 лет до события (некоторые ученые считают это легендой, доказывая, что уровень развития науки во времена Фалеса еще не позволял предсказывать затмения). В честь Фалеса названа малая планета
6001 Thales.
Слайд 26Фалес решил следующие задачи.
Предложил способ определения расстояния до корабля на море.
Вычислил
высоту египетской пирамиды Хеопса по длине отбрасываемой тени.
Доказал равенство углов при основании равнобедренного треугольника.
Ввел понятие движения, в частности поворота.
Доказал второй признак равенства треугольников и впервые применял его в задаче.
Теорема Фалеса о равных отрезках, отсекаемых параллельными прямыми на сторонах угла.
Доказал равенство углов при основании равнобедренного треугольника.
Ввел понятие движения, в частности поворота.
Доказал второй признак равенства треугольников и впервые применял его в задаче.
Теорема Фалеса о равных отрезках, отсекаемых параллельными прямыми на сторонах угла.
Слайд 27
Задача об измерении высоты пирамиды
Однажды, отправившись по торговым делам в Египет,
он задержался там на несколько лет. Случилось так, что фараон пожелал узнать высоту пирамиды, но никто не мог ее определить. Фалес смог легко справиться с задачей.
Выбрав день и час, когда его собственная тень стала равной его росту, он измерил тень, отбрасываемую пирамидой, и установил, что длина тени от центра основания пирамиды до ее вершины была равна высоте этой пирамиды.
Фараон и его приближенные изумились такому достаточно простому решению.
Выбрав день и час, когда его собственная тень стала равной его росту, он измерил тень, отбрасываемую пирамидой, и установил, что длина тени от центра основания пирамиды до ее вершины была равна высоте этой пирамиды.
Фараон и его приближенные изумились такому достаточно простому решению.
Слайд 28«Начала» Евклида
Центральное место среди античных трудов по геометрии занимают составленные
около
300 до н. э. «Начала» Евклида. Этот труд более двух тысячелетий считался образцовым изложением в духе аксиоматического метода: все положения выводятся логическим путём из небольшого числа явно указанных и не доказываемых предположений — аксиом.
Слайд 29Сочинение Евклида «Начала» почти 2000 лет служило основной книгой, по которой
изучали геометрию.
В «Началах» были систематизированы
известные к тому времени
геометрические сведения, и
геометрия впервые предстала
как математическая наука.
Слайд 30 Своими учебниками (то
есть книгами «Начала») Евклид охватил всю элементарную математику той эпохи. «Начала» состоят из 13 книг.
Первые четыре посвящены геометрии на плоскости. Каждую книгу он начинает с пяти аксиом и постулатов. Вспомните их! В первой книге излагается планиметрия прямолинейных фигур: устанавливаются их свойства, заканчивается прямой и обратной теоремой Пифагора. Во второй книге излагается основы геометрической алгебры. Третья книга посвящена свойствам круга, в четвертой строятся правильные п-угольники при п = 3, 4, 5, 6, 10, 15. Исключительное изящное построение правильного 15-угольника принадлежит самому Евклиду.
11 книга посвящена стереометрии. Она содержит основные теоремы о прямых и плоскостях в трехмерном пространстве, задачи на построение, например как опустить перпендикуляр из данной точки на данную плоскость.
12 книга посвящена решению задачи о квадратуре круга. 13 книга излагает учение о правильных многогранниках. В целом творение Евклида величественно. Созданная им система просуществовала более двух тысяч лет. Вплоть до XX века геометрию преподавали по популярным переводам этой книги. Но последующие математики не во всем соглашались с системой аксиом и определений и пытались ее улучшить. Некоторые оказались ненужные, например, что прямые углы равны.
Это очевидно из других аксиом. Особенное неудовлетворение всегда вызывал пятый постулат, утверждавший: что через любую точку плоскости можно провести только одну прямую параллельную данной. Многие считали ее теоремой и пытались ее неудачно доказать.
Первые четыре посвящены геометрии на плоскости. Каждую книгу он начинает с пяти аксиом и постулатов. Вспомните их! В первой книге излагается планиметрия прямолинейных фигур: устанавливаются их свойства, заканчивается прямой и обратной теоремой Пифагора. Во второй книге излагается основы геометрической алгебры. Третья книга посвящена свойствам круга, в четвертой строятся правильные п-угольники при п = 3, 4, 5, 6, 10, 15. Исключительное изящное построение правильного 15-угольника принадлежит самому Евклиду.
11 книга посвящена стереометрии. Она содержит основные теоремы о прямых и плоскостях в трехмерном пространстве, задачи на построение, например как опустить перпендикуляр из данной точки на данную плоскость.
12 книга посвящена решению задачи о квадратуре круга. 13 книга излагает учение о правильных многогранниках. В целом творение Евклида величественно. Созданная им система просуществовала более двух тысяч лет. Вплоть до XX века геометрию преподавали по популярным переводам этой книги. Но последующие математики не во всем соглашались с системой аксиом и определений и пытались ее улучшить. Некоторые оказались ненужные, например, что прямые углы равны.
Это очевидно из других аксиом. Особенное неудовлетворение всегда вызывал пятый постулат, утверждавший: что через любую точку плоскости можно провести только одну прямую параллельную данной. Многие считали ее теоремой и пытались ее неудачно доказать.
«Начала»Евклида
Слайд 31Средние века
Средние века немного дали геометрии, и следующим великим событием в
её истории стало открытие Декартом в XVII веке координатного метода («Рассуждение о методе», 1637). Точкам сопоставляются наборы чисел, это позволяет изучать отношения между формами методами алгебры. Так появилась аналитическая геометрия, изучающая фигуры и преобразования, которые в координатах задаются алгебраическими уравнениями.
Примерно одновременно с этим Паскалем и Дезаргом начато исследование свойств плоских фигур, не меняющихся при проектировании с одной плоскости на другую. Этот раздел получил название проективной геометрии.
Метод координат лежит в основе появившейся несколько позже дифференциальной геометрии, где фигуры и преобразования все ещё задаются в координатах, но уже произвольными достаточно гладкими функциями.
Примерно одновременно с этим Паскалем и Дезаргом начато исследование свойств плоских фигур, не меняющихся при проектировании с одной плоскости на другую. Этот раздел получил название проективной геометрии.
Метод координат лежит в основе появившейся несколько позже дифференциальной геометрии, где фигуры и преобразования все ещё задаются в координатах, но уже произвольными достаточно гладкими функциями.
Слайд 32Геометрия Лобачевского
В 1826 году великий русский математик Николай
Иванович Лобачевский поставил точку в проблеме пятого постулата. Вместо него он принял допущение, согласно которому в плоскости можно построить, по крайней мере, две прямые, не пересекающиеся. Дальнейшие его рассуждения привели его к новой безупречной геометрической системе, называемой сейчас геометрией Лобачевского. В его геометрии сумма углов треугольника меньше 180°, в ней нет подобных фигур. В ней существуют треугольники с попарно параллельными сторонами.
Слайд 33
Никола́й Ива́нович Лобаче́вский (20 ноября
(1 декабря) 1792, Нижний Новгород —
12 (24) февраля 1856, Казань), великий русский математик, создатель геометрии Лобачевского, деятель университетского образования и народного просвещения. Известный английский математик Уильям Клиффорд назвал Лобачевского «Коперником геометрии».
Слайд 36Расчеты современных ученых показывают, что все, связанное с расположением трех главных
пирамид, а может быть, и всех других, что находятся на плато Гизы, отнюдь не случайно: их проектная высота, углы наклона, периметр, даже взаимное расположение на земле - все эти параметры связаны друг с другом, и были выбраны сознательно, с особым смыслом.
То же самое можно сказать и о числе "пи", которое, утверждает аббат Море, можно получить, сложив четыре стороны основания Великой пирамиды, длина каждой из которых, по его мнению, составляет 232,805 метра, и затем разделив полученный результат на две высоты пирамиды.
Пирамиды служили фараонам, согласно их религии, лестницей, по которой они восходили на небо. Поэтому самые древние пирамиды были ступенчатыми, имели форму лестниц, и только у более поздних стены гладкие. Почему это произошло, до сих пор не выяснено.
Исследователей, пытавшихся выяснить, каким образом древние строители смогли воздвигнуть такое грандиозное сооружение, да ещё не просто воздвигнуть, а придать ему геометрически правильную форму пирамиды, всё это ставило в тупик.
То же самое можно сказать и о числе "пи", которое, утверждает аббат Море, можно получить, сложив четыре стороны основания Великой пирамиды, длина каждой из которых, по его мнению, составляет 232,805 метра, и затем разделив полученный результат на две высоты пирамиды.
Пирамиды служили фараонам, согласно их религии, лестницей, по которой они восходили на небо. Поэтому самые древние пирамиды были ступенчатыми, имели форму лестниц, и только у более поздних стены гладкие. Почему это произошло, до сих пор не выяснено.
Исследователей, пытавшихся выяснить, каким образом древние строители смогли воздвигнуть такое грандиозное сооружение, да ещё не просто воздвигнуть, а придать ему геометрически правильную форму пирамиды, всё это ставило в тупик.
Пирамиды