решению задач С2 вариантов ЕГЭ
- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад на тему Призентация Применение метода координат к решению заданий С2 ЕГЭ
Содержание
- 1. Призентация Применение метода координат к решению заданий С2 ЕГЭ
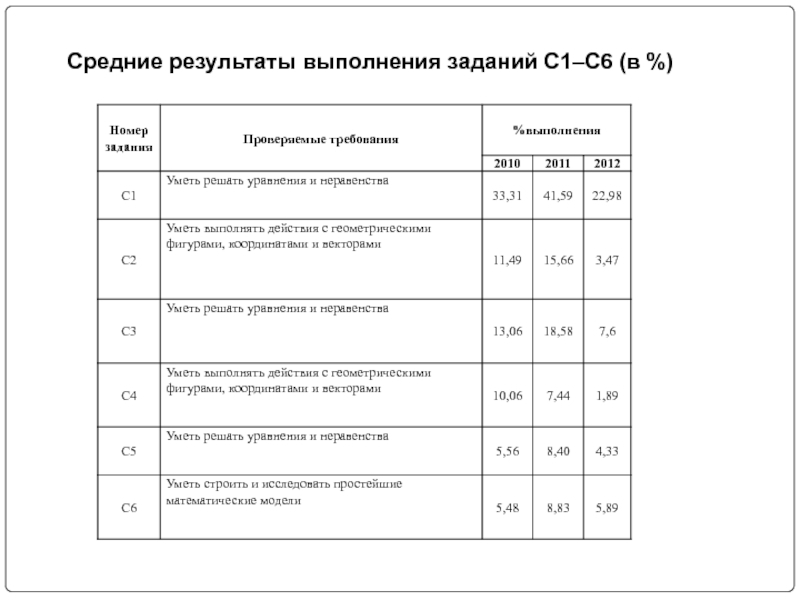
- 2. Средние результаты выполнения заданий С1–С6 (в %)
- 3. Критерии оценивания С2.
- 4. Необходимые умения :Вводить систему координат.Вычислять координаты точек.Вычислять
- 5. Необходимые умения:7. Находить углы в пространстве:между двумя прямыми;между прямой и плоскостью;между двумя плоскостями.8. Вычислять площадь треугольника.
- 6. 1. В правильной треугольной пирамиде МАВС все
- 7. Опорная задача. Дан куб АВСДА1В1С1Д1.Найти координаты векторов нормали к плоскостям:АВСДА1В1С1Д1АА1В1ВВВ1С1СВДС1zyxДС1Д1В1СА1АВ
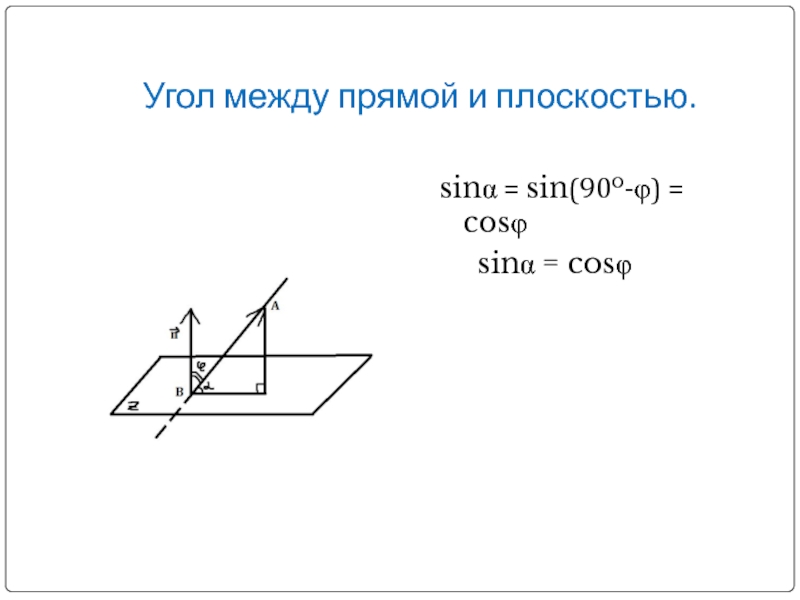
- 8. Угол между прямой и плоскостью.sinα = sin(90o-φ) = cosφ sinα = cosφ
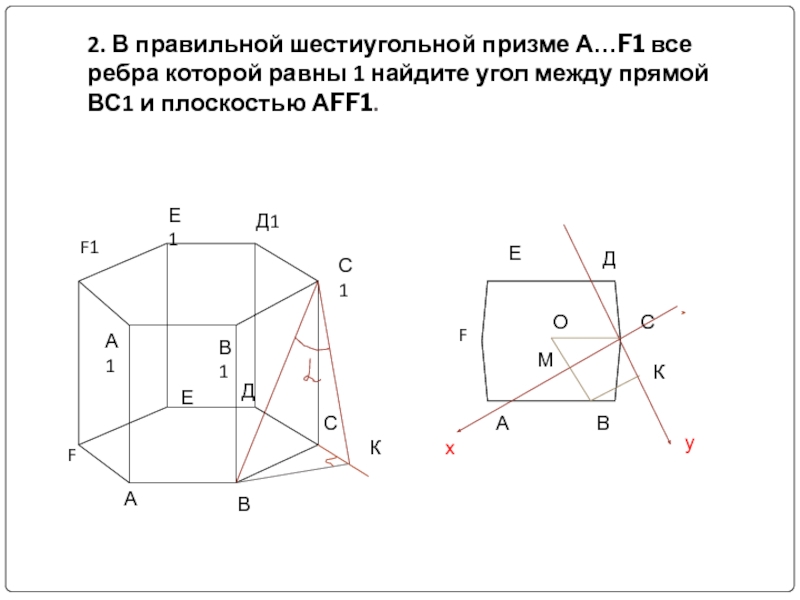
- 9. 2. В правильной шестиугольной призме А…F1 все
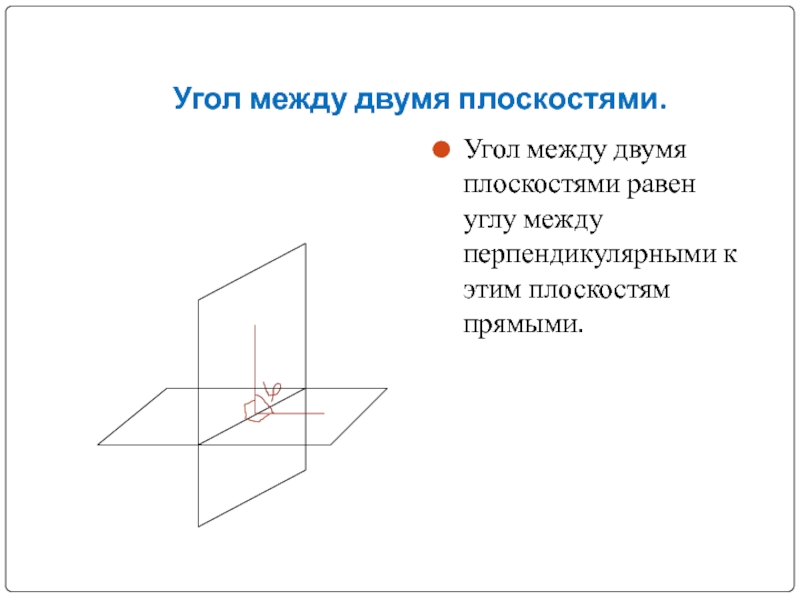
- 10. Угол между двумя плоскостями.Угол между двумя плоскостями равен углу между перпендикулярными к этим плоскостям прямыми.
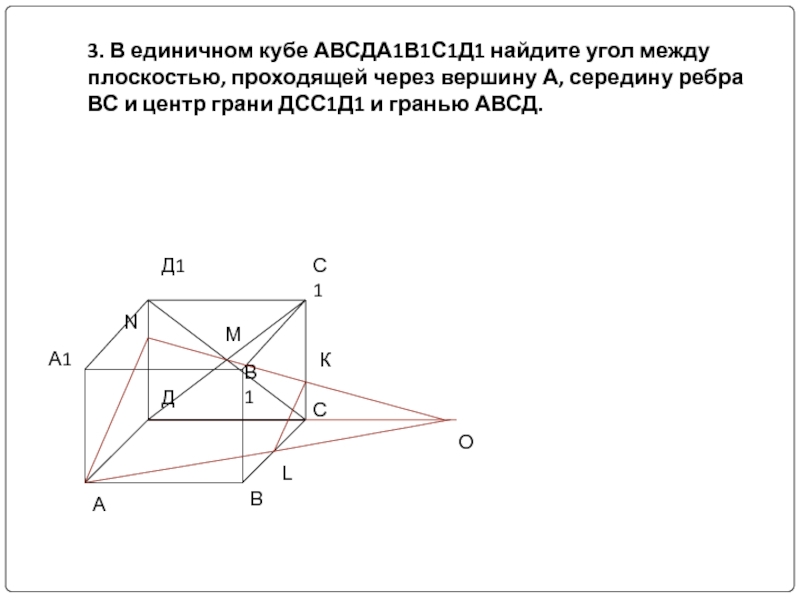
- 11. 3. В единичном кубе АВСДА1В1С1Д1 найдите угол
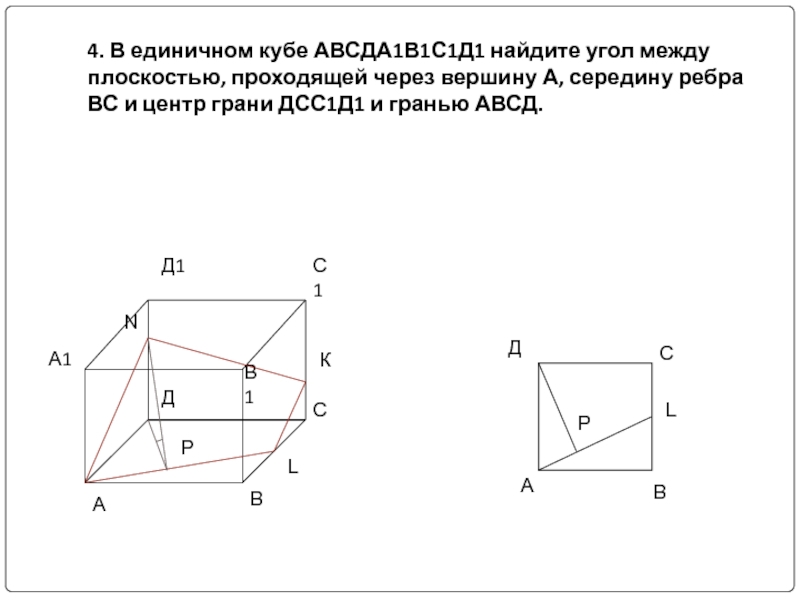
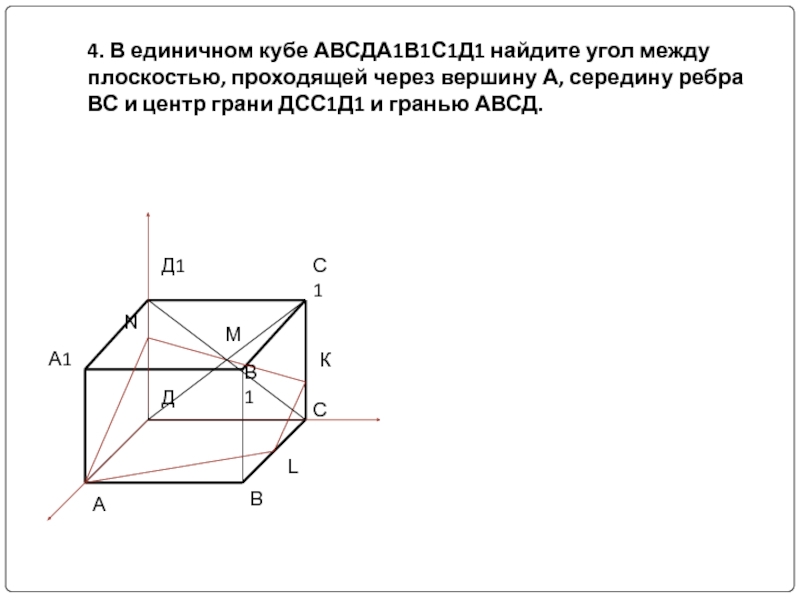
- 12. 4. В единичном кубе АВСДА1В1С1Д1 найдите угол
- 13. 4. В единичном кубе АВСДА1В1С1Д1 найдите угол
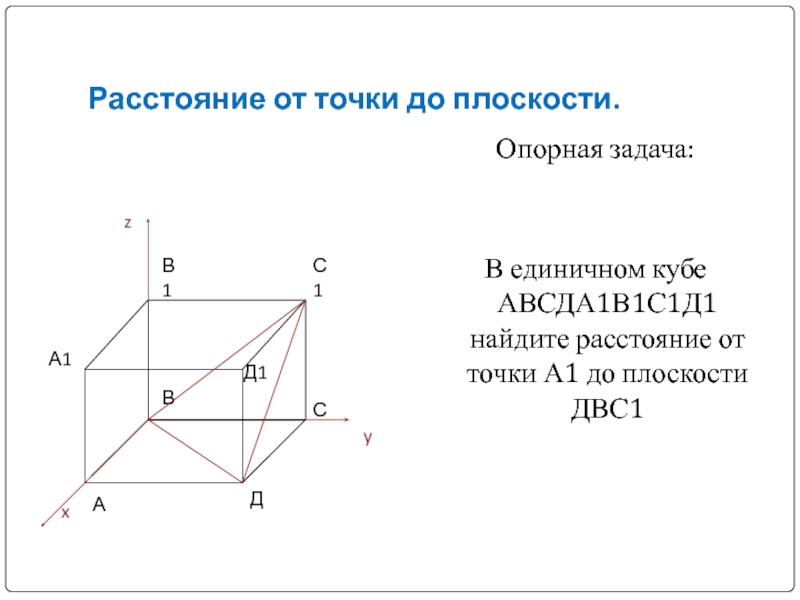
- 14. Расстояние от точки до плоскости.Опорная задача:В единичном
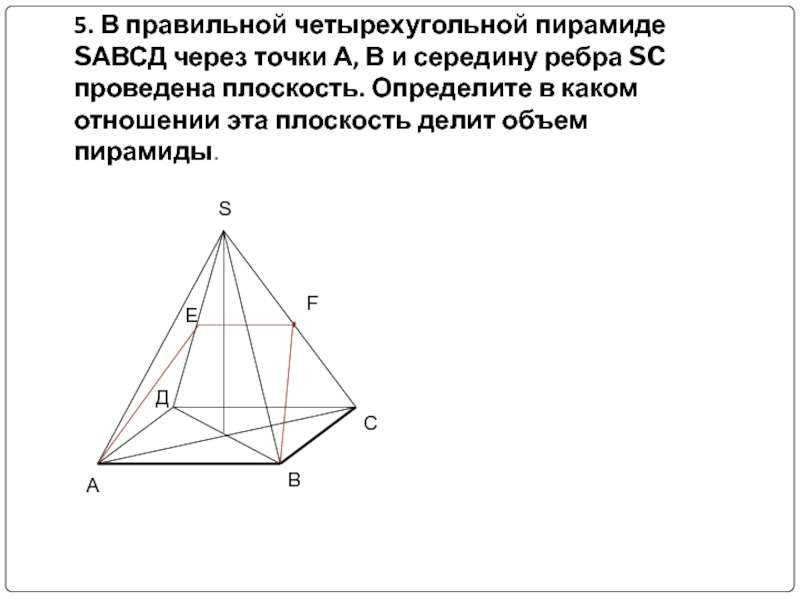
- 15. 5. В правильной четырехугольной пирамиде SАВСД через
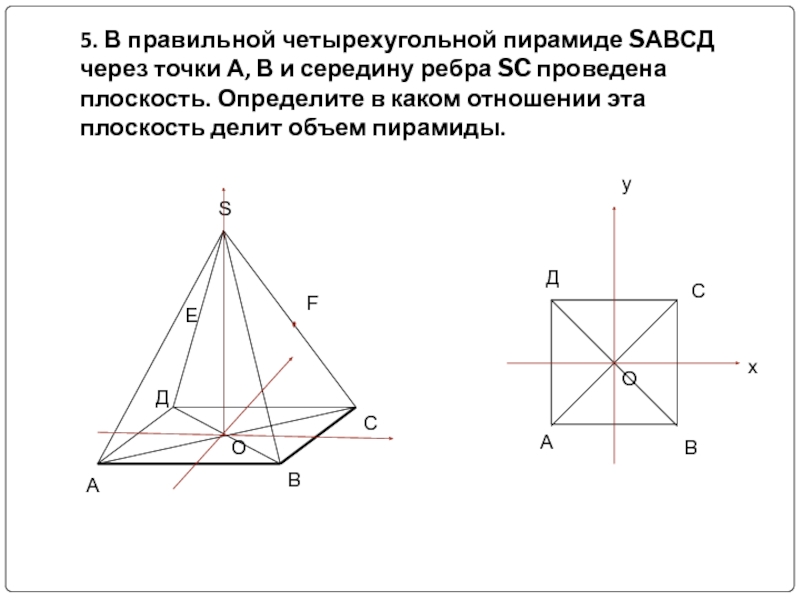
- 16. 5. В правильной четырехугольной пирамиде SАВСД через
- 17. Деление отрезка в заданном отношении.
- 18. ЕГЭ 2013. В правильной четырехугольной пирамиде МАВСД
- 19. Расстояние между скрещивающимися прямыми.В кубе АВСДА1В1С1Д1 найдите
- 20. Вычисление площади треугольника в пространстве. Вычислите площадь треугольника, заданного координатами вершин.А(1;4;5)В(-1;2;3)С(0;4;-2)
- 21. Слайд 21
- 22. Слайд 22
Средние результаты выполнения заданий С1–С6 (в %)
Слайд 4Необходимые умения :
Вводить систему координат.
Вычислять координаты точек.
Вычислять координаты вектора.
Вычислять длину вектора.
Находить
координаты середины отрезка.
Находить расстояний в пространстве:
между двумя точками;
от точки до прямой;
от точки до плоскости;
между скрещивающимися прямыми.
Находить расстояний в пространстве:
между двумя точками;
от точки до прямой;
от точки до плоскости;
между скрещивающимися прямыми.
Слайд 5Необходимые умения:
7. Находить углы в пространстве:
между двумя прямыми;
между прямой и плоскостью;
между
двумя плоскостями.
8. Вычислять площадь треугольника.
8. Вычислять площадь треугольника.
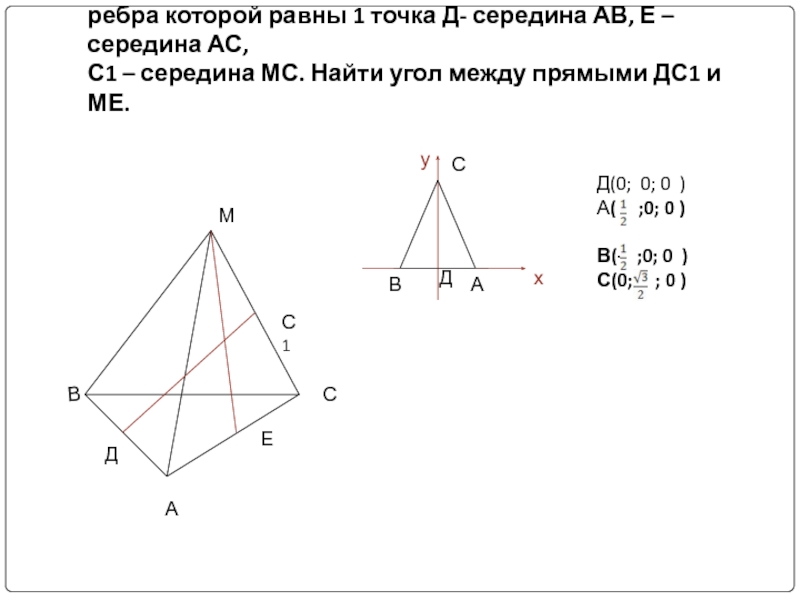
Слайд 61. В правильной треугольной пирамиде МАВС все ребра которой равны 1
точка Д- середина АВ, Е – середина АС,
С1 – середина МС. Найти угол между прямыми ДС1 и МЕ.
А
С
В
М
С1
Е
Д
А
В
С
х
у
Д(0; 0; 0 )
А( ;0; 0 )
В(- ;0; 0 )
С(0; ; 0 )
Д
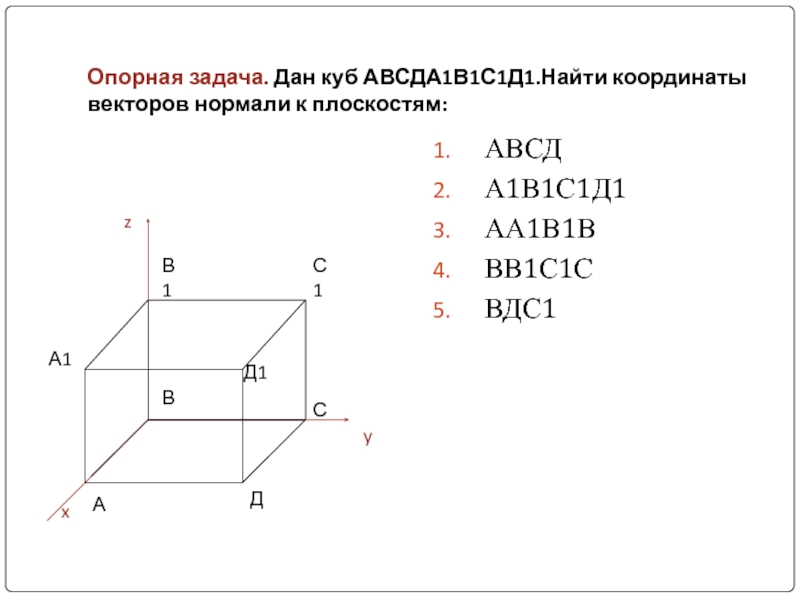
Слайд 7Опорная задача. Дан куб АВСДА1В1С1Д1.Найти координаты векторов нормали к плоскостям:
АВСД
А1В1С1Д1
АА1В1В
ВВ1С1С
ВДС1
z
y
x
Д
С1
Д1
В1
С
А1
А
В
Слайд 92. В правильной шестиугольной призме А…F1 все ребра которой равны 1
найдите угол между прямой ВС1 и плоскостью АFF1.
F
А
В
С
Д
Е
А1
В1
С1
Д1
Е1
F1
А
В
С
Д
Е
F
х
у
О
К
М
К
Слайд 10Угол между двумя плоскостями.
Угол между двумя плоскостями равен углу между перпендикулярными
к этим плоскостям прямыми.
Слайд 113. В единичном кубе АВСДА1В1С1Д1 найдите угол между плоскостью, проходящей через
вершину А, середину ребра ВС и центр грани ДСС1Д1 и гранью АВСД.
В
С1
В1
Д1
С
А1
А
Д
N
К
М
О
L
Слайд 124. В единичном кубе АВСДА1В1С1Д1 найдите угол между плоскостью, проходящей через
вершину А, середину ребра ВС и центр грани ДСС1Д1 и гранью АВСД.
В
С1
В1
Д1
С
А1
А
Д
N
К
L
Р
А
В
С
Д
L
P
Слайд 134. В единичном кубе АВСДА1В1С1Д1 найдите угол между плоскостью, проходящей через
вершину А, середину ребра ВС и центр грани ДСС1Д1 и гранью АВСД.
В
С1
В1
Д1
С
А1
А
Д
N
К
L
М
Слайд 14Расстояние от точки до плоскости.
Опорная задача:
В единичном кубе АВСДА1В1С1Д1 найдите расстояние
от точки А1 до плоскости ДВС1
z
y
x
Д
С1
Д1
В1
С
А1
А
В
Слайд 155. В правильной четырехугольной пирамиде SАВСД через точки А, В и
середину ребра SC проведена плоскость. Определите в каком отношении эта плоскость делит объем пирамиды.
А
В
С
Д
S
F
Е
Слайд 165. В правильной четырехугольной пирамиде SАВСД через точки А, В и
середину ребра SC проведена плоскость. Определите в каком отношении эта плоскость делит объем пирамиды.
А
В
С
Д
S
F
Е
х
у
А
В
С
Д
О
О
Слайд 17Деление отрезка в заданном отношении.
АЕ:ЕВ=2:1
А(1;2;5 )
В(4;3;-1)
Определите координаты точки Е, которая делит АВ в заданном отношении.
А
В
Е
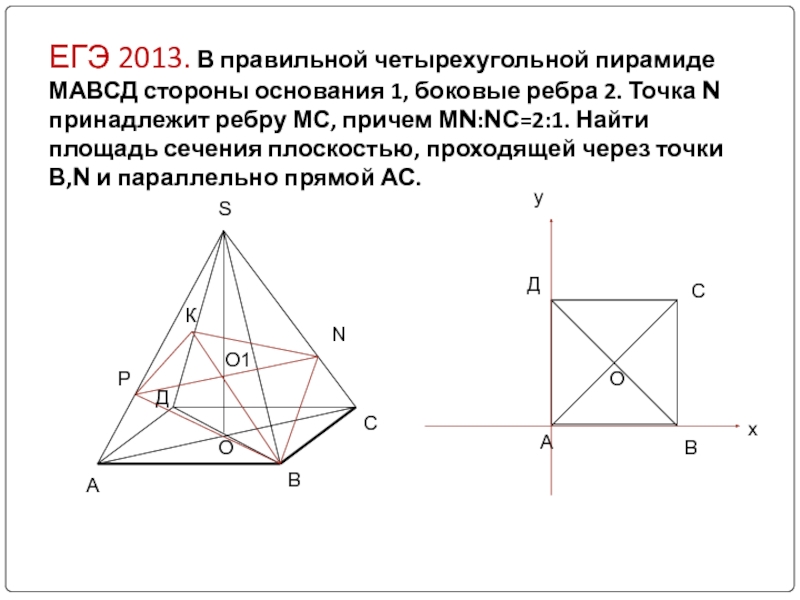
Слайд 18ЕГЭ 2013. В правильной четырехугольной пирамиде МАВСД стороны основания 1, боковые
ребра 2. Точка N принадлежит ребру МС, причем МN:NС=2:1. Найти площадь сечения плоскостью, проходящей через точки В,N и параллельно прямой АС.
А
В
С
Д
S
К
х
у
А
В
С
Д
О
О
Р
N
О1
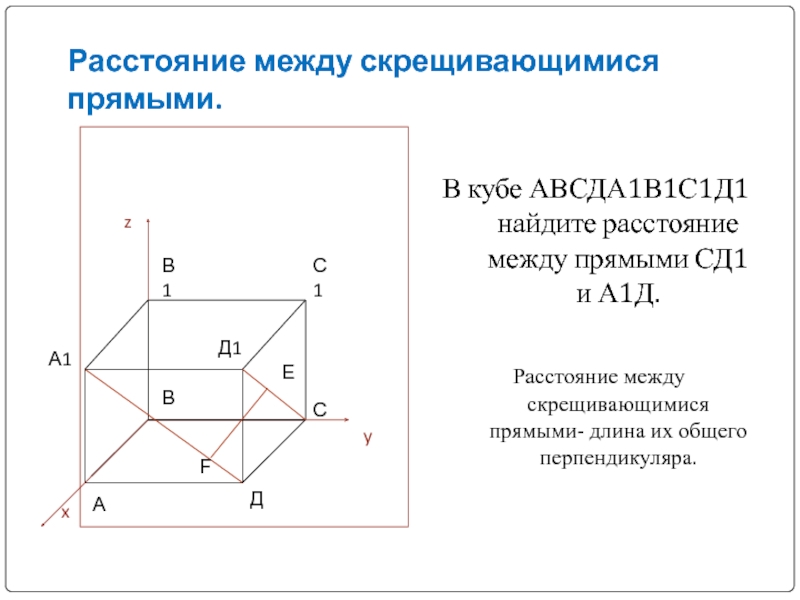
Слайд 19Расстояние между скрещивающимися прямыми.
В кубе АВСДА1В1С1Д1 найдите расстояние между прямыми СД1
и А1Д.
Расстояние между скрещивающимися прямыми- длина их общего перпендикуляра.
Расстояние между скрещивающимися прямыми- длина их общего перпендикуляра.
z
y
x
Д
С1
Д1
В1
С
А1
А
В
Е
F
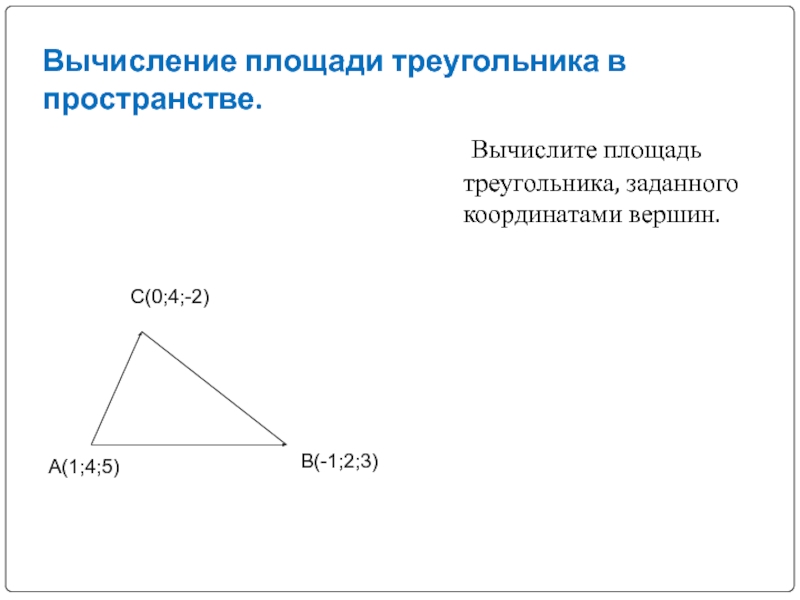
Слайд 20Вычисление площади треугольника в пространстве.
Вычислите площадь треугольника, заданного
координатами вершин.
А(1;4;5)
В(-1;2;3)
С(0;4;-2)
