Шабалина Л.А.,
учитель математики
- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад на тему Приёмы устного счёта
Содержание
- 1. Приёмы устного счёта
- 2. Цели устных вычислений в обучении математикеповышение общего
- 3. Задачи устного счетавключение в работу всех учащихся;возбуждение
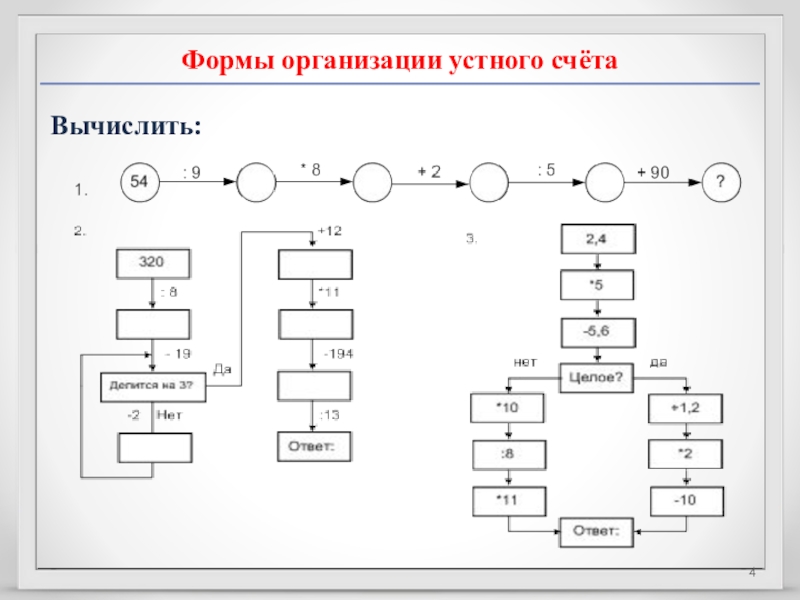
- 4. Формы организации устного счётаВычислить:
- 5. Формы организации устного счётаВосстановить пропущенные цифры: 5
- 6. Формы организации устного счётаНайти ошибку:
- 7. Формы организации устного счёта1. Вычислить рационально.44 –
- 8. Формы организации устного счётаТестовые вопросыДано число 3,6.1)
- 9. Формы организации устного счётаТестовые заданияВместо квадратиков запишите такие числа, чтобы равенства оказались верными:
- 10. Формы организации устного счётаТренажёрыКарточки устного счета:
- 11. Формы организации устного счётаТренажёры1)Используя формулы Р =
- 12. Формы организации устного счётаОнлайн тренажёрыhttps://arithmetic.zetamac.com/ http://www.sposobnostiuma.com https://chisloboi.ru/ https://matematika.club
- 13. Формы организации устного счётаИгровые моментыБеглый счётРавный счётиили
- 14. Формы организации устного счётаИгровые моментыСчёт - дополнение
- 15. Формы организации устного счётаИгровые моментыМолчанкаЭстафета
- 16. Формы организации устного счётаИгровые моментыТоропись, да не
- 17. Формы организации устного счётаИгровые моментыКто первый скажет
- 18. Приемы быстрых вычислений Если одно из слагаемых
- 19. Приемы быстрых вычислений Применение распределительного закона умножения
- 20. Приемы быстрых вычислений Сложение столбцами.
- 21. Приемы быстрых вычислений Умножение на 0,5; 0,25;
- 22. Приемы быстрых вычислений Умножение чисел на 11
- 23. Приемы быстрых вычислений Умножение на 5, 25,
- 24. Занимательные формы устного счетаЗанимательное умножение: Парад чисел:11
- 25. Занимательные формы устного счетаМагические квадраты: Сумма чисел
- 26. Нестандартные приемы устного счета 1) Таблица умножения
- 27. Нестандартные приемы устного счета 3) Метод Ферроля4) Крест накрест (умножение чисел, близких к 100)
- 28. Формы организации устного счёта при изучении алгебры1.
- 29. Формы организации устного счёта при изучении алгебры3.
- 30. Формы организации устного счёта при изучении алгебры6.
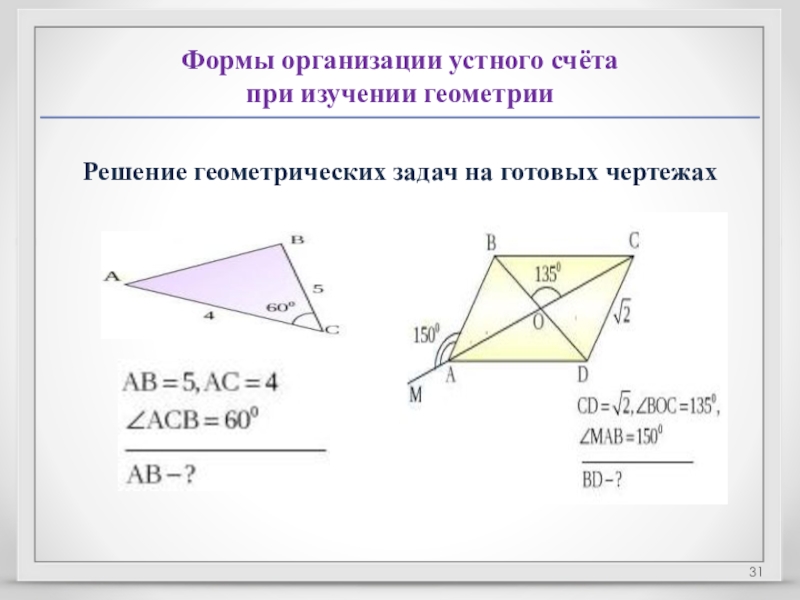
- 31. Формы организации устного счёта при изучении геометрииРешение геометрических задач на готовых чертежах
- 32. Спасибо за внимание!
Слайд 1Муниципальное бюджетное общеобразовательное учреждение
«Средняя общеобразовательная школа №89 г. Челябинска»
Приемы устного счёта
Слайд 2Цели устных вычислений в обучении математике
повышение общего уровня математического образования и
активизация мыслительной деятельности учащихся;
Слайд 3Задачи устного счета
включение в работу всех учащихся;
возбуждение интереса;
развитие памяти, речи, внимания;
стимулирование
совершенствование навыков самостоятельной работы;
развитие мышления;
развитие навыков быстрого применения знаний, правил, формул, теорем для конкретного примера, расчёта, задачи.
Слайд 6Формы организации устного счёта
Найти ошибку:
х = 341 + 111, у = 24,1 +12,9, 0,75 ≈ 0,7
х = 452. у = 36,10. 2,99 ≈ 3,0
Ответ: 452. Ответ: 36,1 8,18 ≈ 8,2
Слайд 7Формы организации устного счёта
1. Вычислить рационально.
44 – (14 + 38);
(212 + 134) – (112 + 34); 25 + 37 – 5; 1,1 * 15;
94427 + 1484) – 327; 5 * 8 * 4 * 125; 2,8 * 9.
2. Найти значения следующих сумм:
1 + 3 = (4);
1 + 3 + 5 = (9);
1 + 3 + 5 + 7 = (16);
1 + 3 + 5 + 7 + 9 = (25);
Уловите закономерность в этих равенствах и, опираясь на них, определите, чему равны суммы
1 + 3 + 5 + 7 + 9 + 11
1 + 3 + 5 + 7 + 9 + 11 + 13
Слайд 8Формы организации устного счёта
Тестовые вопросы
Дано число 3,6.
1) Назовите число: а)
2) Представьте число в виде суммы:
а) двух равных слагаемых;
б) двух неравных слагаемых;
в) трех равных слагаемых;
г) трех неравных слагаемых.
3) Назовите дополнение числа 3,6
а) до 10; б) до 36.
4) представьте число 3,6 в виде
а) произведения двух чисел;
б) разности двух чисел;
в) частного двух чисел.
Слайд 9Формы организации устного счёта
Тестовые задания
Вместо квадратиков запишите такие числа, чтобы равенства
Слайд 11Формы организации устного счёта
Тренажёры
1)Используя формулы Р = 2(а + b) и
2)Вычислите устно:
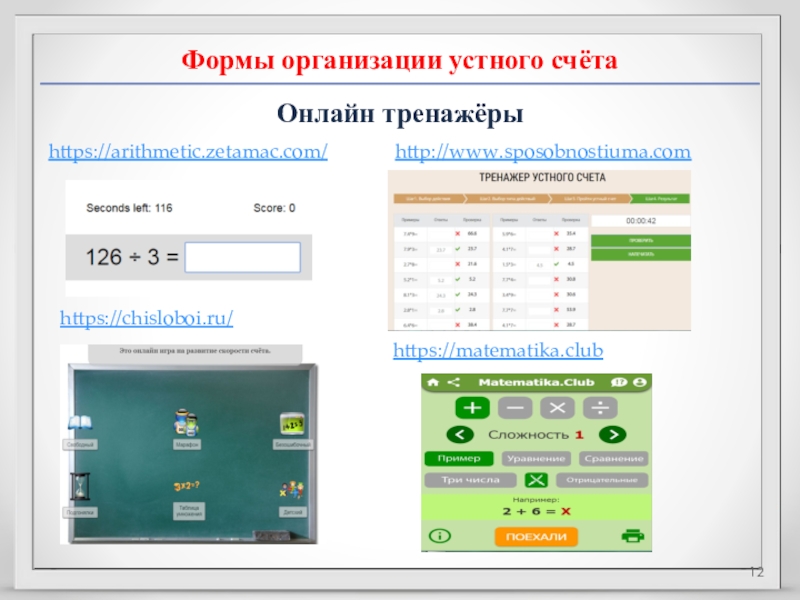
Слайд 12Формы организации устного счёта
Онлайн тренажёры
https://arithmetic.zetamac.com/
http://www.sposobnostiuma.com
https://chisloboi.ru/
https://matematika.club
Слайд 14Формы организации устного счёта
Игровые моменты
Счёт - дополнение
Лесенка
Учитель:
1 0,5
0,3 1,2
0,7 0,8
1,4 0,1
1,1 0,4
Слайд 15Формы организации устного счёта
Игровые моменты
Молчанка
Эстафета
5,6 * 10 3,7 * 10
0,11 * 10 0,85 * 10
1,7 * 100 2,3 * 100
0,518 * 100 0,371 * 100
0,0083 * 1000 0,0751 * 1000
169 : 10 6,3 : 10
2,6 : 100 8,5 : 100
89 : 1000 11 : 1000
0,37 : 10000 1,72 : 10000
Слайд 16Формы организации устного счёта
Игровые моменты
Торопись, да не ошибись.
Игра – математический
Не зевай.
2,5 + 3,7 = (6,2)
… - 5,1 =
… + 3,09 =
… - 0,19 =
… * 2,2 =
Слайд 17Формы организации устного счёта
Игровые моменты
Кто первый скажет 100?
Двое поочередно
Например, первый скажет - 7 , второй – 9, при сложении их получится 16, затем первый говорит – 5, получится – 21, второй говорит – 8, получится – 29 и т.д. Победителем станет тот, кто первый скажет 100.
Не сбейся!
В игре участвуют все желающие. Они должны по очереди называть
натуральные числа, которые обладают хотя бы одним из свойств:
а) В записи числа есть цифра 3;
б) Число делится на 3.
Например: 3, 6, 9, 12, 13, 15, 18, 21, 23, 24,…
Учащийся, допустивший ошибку или пропуск числа, выбывает из игры.
Слайд 18Приемы быстрых вычислений
Если одно из слагаемых увеличить на несколько единиц,
364 + 592 = 364 + ( 592 + 8 ) – 8 = 364 + 600 – 8 = 956.
Если одно из слагаемых увеличить на несколько единиц, а другое уменьшить на столько же единиц, то сумма не изменится.
997 + 856 = ( 997 + 3 ) + ( 856 – 3 ) = 1000 + 853 = 1853.
Если вычитаемое увеличить на несколько единиц и уменьшаемое увеличить на столько же единиц, то разность не изменится.
1351 – 994 = ( 1351 + 6 ) – ( 994 + 6 ) = 1357 – 1000 = 357.
Если от суммы двух чисел отнять разность этих же чисел, то в результате получится удвоенное меньшее число.
( 57 + 23 ) – ( 57 – 23 ) = 46.
Если к сумме двух чисел прибавить их разность, то в результате получится удвоенное большее число.
( 74 + 26 ) + ( 74 – 26 ) = 148.
Слайд 19Приемы быстрых вычислений
Применение распределительного закона умножения относительно
сложения и вычитания.
7 * 196 = 7 * ( 200 – 4 ) = 1400 – 28.
Произведение двух чисел не изменится, если первый множитель
умножить, а второй разделить на одно и то же натуральное число.
13 * 64 = 26 * 32 = 52 * 16 = …. = 832 * 1;
24 * 17 = (24 * 16) + 24 = ( 48 * 8 ) + 24 = ( 96 * 4 ) + 24 = ( 192 * 2 ) + 24 =
= ( 384 * 1 ) + 24 = 384 + 24 = 408.
Делимое и делитель можно умножить или разделить нацело на
одно и то же натуральное число – частное от этого не изменится.
48 : 24 = 2
(48 * 2) : (24*2) = 96 : 48 = 2
(48 : 2) : (24 : 2) = 24 : 12 = 2
Слайд 21Приемы быстрых вычислений
Умножение на 0,5; 0,25; 0,125; 1,5; 2,5.
Чтобы число
84*1,5 =84+42=126
Чтобы число умножить на 2,5 нужно к числу прибавить его же и его половину:
84* 2,5 =84+84+42=210
Чтобы число умножить на 0,5; 0,25; 0,125 надо это число разделить на 2, на 4, на 8:
98*0,5=49 124*0,25=31 168*0,125=21
Слайд 22Приемы быстрых вычислений
Умножение чисел на 11
2) 4 + 5 = 9, пишем 9
3) пишем 5
б) 124 * 11 = 1(1+2)(2+4)4 = 1364
в) 58 * 11 = 638 1) пишем 8
2) 5 + 8 = 13, пишем 3, помним 1
3) 5 + 1 = 6, пишем 6
Умножение двузначного числа на 101
73 * 101 = 7373
48 * 101 = 4848
Умножение на 9, 99, 999
а) 286 * 9 = 2860 – 286 = 2574;
б) 23 * 99 = 2300 – 23 = 2277;
в) 18 * 999 = 1800 – 18 = 17982.
Слайд 23Приемы быстрых вычислений
Умножение на 5, 25, 125
а) 46 * 5
б) 48 * 25 = 48 : 4 * 100 = 1200;
в) 32 * 125 = 32 : 8 * 1000 = 4000;
г) 53 * 5 = (53 : 2 = 26 и 1-остаток) = 26 * 10 + 1 * 5 = 265;
д) 43 * 25 = (43 : 4 = 10 и 3-остаток) = 10 * 100 + 3 * 25 = 1075;
е) 66 * 125 = (66 : 8 = 8 и 2-остаток) = 8 * 1000 + 2 * 125 = 8250.
Деление на 5, 25, 125
а) 220 : 5 = 220 * 2 : 10 = 44;
б) 1300 : 25 = 1300 * 4 : 100 =52;
в) 9250 : 125 = 9250 * 8 : 1000 = 74.
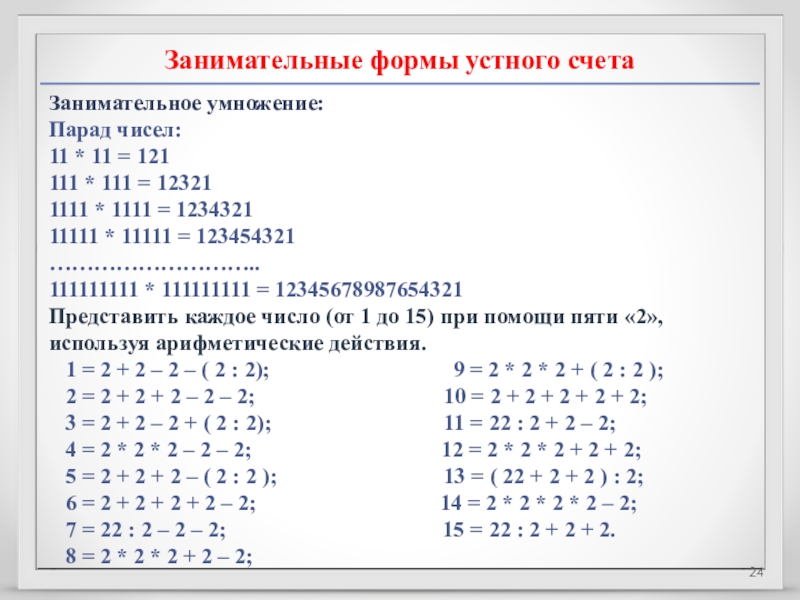
Слайд 24Занимательные формы устного счета
Занимательное умножение:
Парад чисел:
11 * 11 = 121
111
1111 * 1111 = 1234321
11111 * 11111 = 123454321
………………………..
111111111 * 111111111 = 12345678987654321
Представить каждое число (от 1 до 15) при помощи пяти «2», используя арифметические действия.
1 = 2 + 2 – 2 – ( 2 : 2); 9 = 2 * 2 * 2 + ( 2 : 2 );
2 = 2 + 2 + 2 – 2 – 2; 10 = 2 + 2 + 2 + 2 + 2;
3 = 2 + 2 – 2 + ( 2 : 2); 11 = 22 : 2 + 2 – 2;
4 = 2 * 2 * 2 – 2 – 2; 12 = 2 * 2 * 2 + 2 + 2;
5 = 2 + 2 + 2 – ( 2 : 2 ); 13 = ( 22 + 2 + 2 ) : 2;
6 = 2 + 2 + 2 + 2 – 2; 14 = 2 * 2 * 2 * 2 – 2;
7 = 22 : 2 – 2 – 2; 15 = 22 : 2 + 2 + 2.
8 = 2 * 2 * 2 + 2 – 2;
Слайд 25Занимательные формы устного счета
Магические квадраты:
Сумма чисел вдоль каждой строки, каждого
и каждой диагонали одинаковы.
а) Составь магический квадрат, состоящий из девяти клеток, в которых размещены числа 2, 4, 6, 8, 10, 12, 14, 16, 18 так, чтобы в любом направлении получилось бы число 30.
б) В клетках квадрата переставить числа так, чтобы по всем направлениям их сумма равна 33.
Слайд 26Нестандартные приемы устного счета
1) Таблица умножения на пальцах
2) Быстрое возведение
оканчивающихся на 5
Слайд 27Нестандартные приемы устного счета
3) Метод Ферроля
4) Крест накрест (умножение чисел,
Слайд 28Формы организации устного счёта
при изучении алгебры
1. Действия над рациональными числами
Назовите числа, из которых можно извлечь квадратный корень:
0,25; 7; -4; 1/3; 0; 0,81; -16; 1/2; 5.
Найдите значение выражения
2. Нахождение числовых значений алгебраических выражений
Сформулировать применяемый закон или свойство арифметического действия и вычислить при данных значениях букв:
Слайд 29Формы организации устного счёта
при изучении алгебры
3. Формулы сокращенного умножения
Используя формулы
201²; 301².
4. Преобразование алгебраических выражений
Умножьте одночлен на многочлен:
3a²x · (-4ax² + x³)
Вынесите общий множитель за скобки:
a² + ab – ac + a
5. Решение уравнений:
у² 9
у + 5 у + 5
Слайд 30Формы организации устного счёта
при изучении алгебры
6. Решение алгебраических задач
Длина прямоугольного
8. Вычисления значений функции:
Функция задана формулой f(x) = х³. Сравните, используя таблицу кубов:
f(3,7) и f(4,2)
f(-7) и f(-6)
f(31) и f(-28)
7. Построение графиков
Построить график функции
у = 2,5х – 1,3.
Табличные значения вычислить устно.