- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад на тему Презинтация по математику на тему Вычесление двойного и тройного интеграла (студентов ВУЗа)
Содержание
- 1. Презинтация по математику на тему Вычесление двойного и тройного интеграла (студентов ВУЗа)
- 2. Замена переменных в двойном интеграле. Двойной интеграл в полярных координатах
- 3. Цель темы:Ознакомить студентов с новой темой, объяснить
- 4. План:Замена переменных в двойном интеграле Двойной интеграл
- 5. ВопросыЧто называется двойным интегралом?Какими свойствами обладает двойной
- 6. Замена двойного интегралаПредположим, что в двойном интеграле
- 7. Слайд 7
- 8. Поскольку параметрические уравнения кривой ABCE параллелограмм, который
- 9. Запишем обозначение Итак, элемент площади
- 10. Пример 1: Измерить порядок интегрирования
- 11. Пусть G = G1UG2 (рис. 6). Тогда каждая прямая x
- 12. Пример 2: Вычислить интегралгде область G ограничена
- 13. Двойной интеграл в полярных координатахПусть на плоскости Оху одновременно
- 14. Для полярной системы координатная сетка представляет собой
- 15. Рассмотрим элементарный участок полярной сетки (рис. 11).
- 16. Замечание.Формулу (2.13) можно получить и по-другому, используя Якобиан
- 17. Теорема: Если область D - является правильной в полярной
- 18. Пример 3: Вычислить двойной интегралгде область D есть первая четверть
- 19. Пример 4: Вычислить двойной интеграл где область D верхняя часть кругаРешение. Перейдем
- 20. Находя первообразные и подставляя пределы окончательно получим:
- 21. ЗнаюХочу узнатьУзнал З Х У
- 22. Заключение В первой части темы
- 23. Задания по пройденной теме1. Изменить порядок интегрирования
- 24. Список используемой литературы1. Фихтенгольц Г.М. Курс дифференциального
Слайд 3Цель темы:
Ознакомить студентов с новой темой, объяснить как заменять двойные интегралы.
С помощью таких тем все больше заинтересовать студентов к математике. Стараться связывать предмет математики с жизненными примерами, что вызывает большой интерес у студентов.
Студенты должны хорошо усвоить данный материал.
Слайд 4План:
Замена переменных в двойном интеграле
Двойной интеграл в полярных координатах
Применение
Вопросы по пройденной теме
Примеры на самостоятельное решение
Список использованной литературы
Слайд 5Вопросы
Что называется двойным интегралом?
Какими свойствами обладает двойной интеграл?
Геометрический смысл двойного интеграла?
Напишите
Слайд 6Замена двойного интеграла
Предположим, что в двойном интеграле
необходимо перейти к
В функции на , иными словами имеются обратные функции
Если область в плоскости на криволинейные параллелограммы. Обозначим на плоскости бесконечно малый прямоугольник
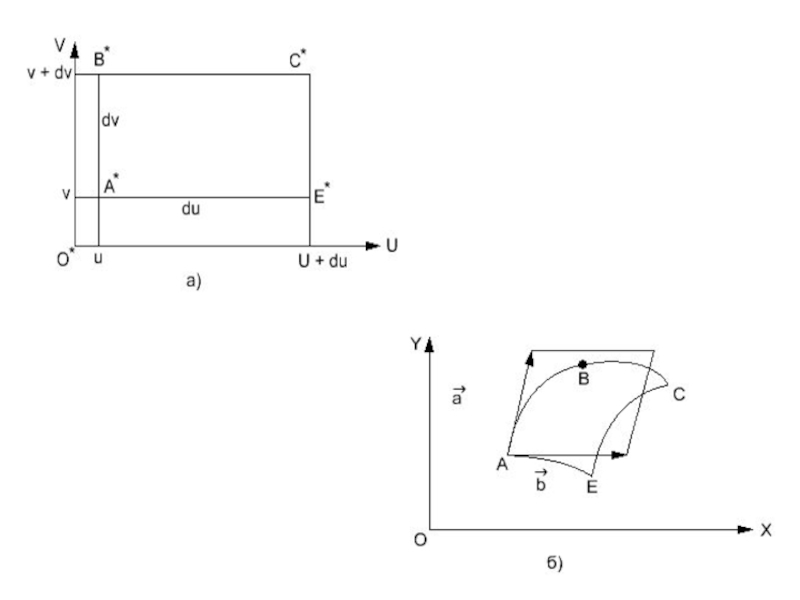
Слайд 8Поскольку параметрические уравнения кривой ABCE параллелограмм, который построен на векторах
В
Слайд 9 Запишем обозначение
Итак, элемент площади
(*)
Запишем формулу замены переменной в двойном интеграле
здесь используется в качестве образа в системе . Определитель именуют якобианом преобразования координат. При ненулевом якобиане, преобразование
имеет смысл или является невырожденным.
Следует отметить, что формула (*) может быть использована и в случае - мерного пространства.
Слайд 10Пример 1: Измерить порядок интегрирования в интеграле
Решение. В
Где
и
Представляют собой дуги параболы
Лежащие выше оси Ox
Лежащие ниже оси Ox
Область интегрирования во втором интеграле имеет вид:
Где кривые
и
Представляют собой дуги параболы
И дугу окружности
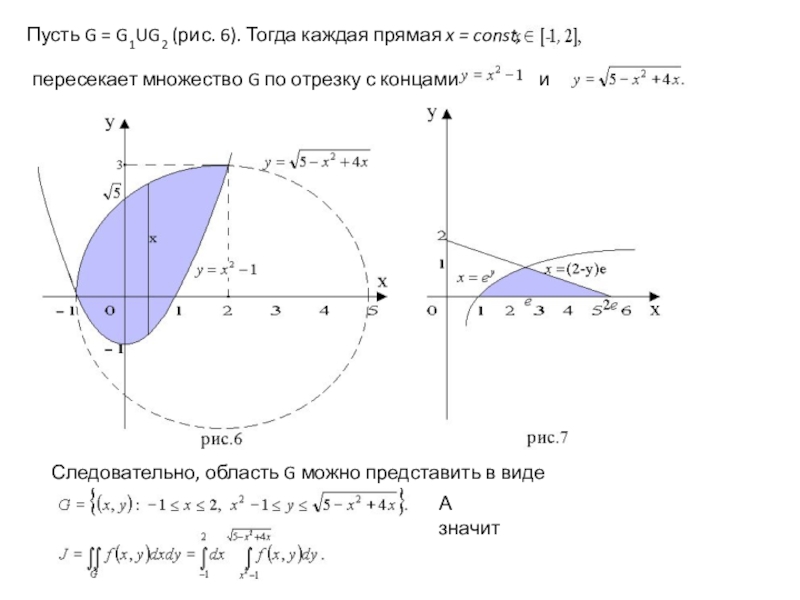
Слайд 11Пусть G = G1UG2 (рис. 6). Тогда каждая прямая x = const,
пересекает множество G
и
Следовательно, область G можно представить в виде
А значит
Слайд 12Пример 2: Вычислить интеграл
где область G ограничена линиями:
и y=0 (Рис.7)
При каждом
значение x меняется от
до x=(2-y)e. Поэтому
Интегрируя теперь функцию
по y в пределах от y = 0 до y = 1, получим
При вычислении интеграла
используем форму интегрирования по частям. Имеем
Слайд 13Двойной интеграл в полярных координатах
Пусть на плоскости Оху одновременно введена и полярная система
Тогда, как известно:
(2.12)
Рис. 2.9
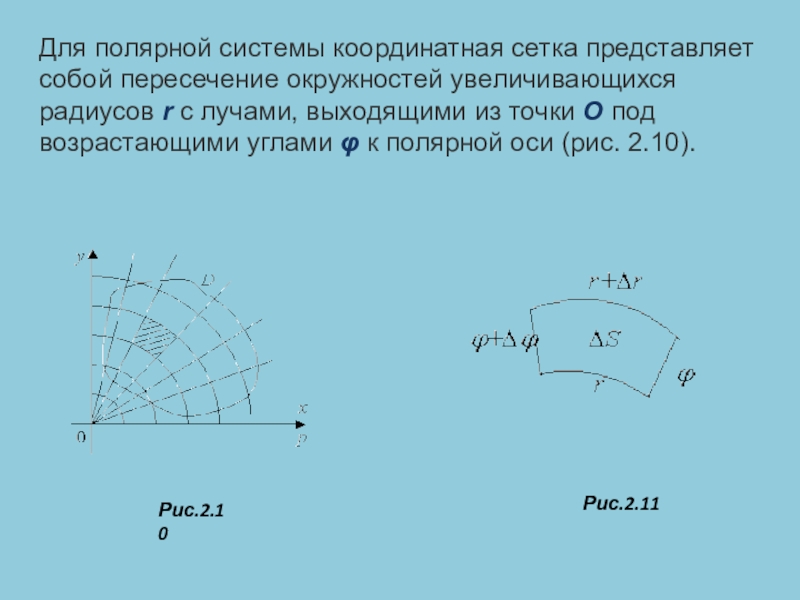
Слайд 14Для полярной системы координатная сетка представляет собой пересечение окружностей увеличивающихся радиусов r с
Рис.2.10
Рис.2.11
Слайд 15Рассмотрим элементарный участок полярной сетки (рис. 11). Тогда его площадь ΔS можно найти как
При Δr → 0, Δφ → 0 получаем ΔS ≈ r · Δr · Δφ. Таким образом, при замене переменных по формуле (2.12) дифференциал площади в полярной системе координат преобразуется так:
2.13
В декартовой системе координат Оху прямоугольная сетка дает dS = dx · dy.
Слайд 16Замечание.
Формулу (2.13) можно получить и по-другому, используя Якобиан J - "коэффициент искажения" площади
Что совпадает с (2.13)
Слайд 17Теорема: Если область D - является правильной в полярной системе координат Оrφ, то двойной
Слайд 18Пример 3: Вычислить двойной интеграл
где область D есть первая четверть круга
Решение. Построим область D в декартовой системе
интеграле перейдем к полярным координатам:
Полярный угол φ в области D изменяется от 0 до
а полярный радиус r – от 0 до R, следовательно:
Слайд 19Пример 4: Вычислить двойной интеграл
где область D верхняя часть круга
Решение. Перейдем к полярным координатам в
Значения переменных φ и r заключены в пределах 0 ≤ φ ≤ π, 0 ≤ r ≤ 1, поэтому
Каждый из линейных интегралов в правой части равенства можно вычислить отдельно, так как пределы постоянны:
Слайд 22Заключение
В первой части темы рассмотрели замену переменных в
Рассмотрели теоретические основы. Привели примеры на измерение порядка интегрирования в интеграле, а также вычисление и применение.
Вторая часть темы двойной интеграл в полярных координатах. Тут ознакомились формулой Якобиан, а так же были приведены примеры.
Слайд 23Задания по пройденной теме
1. Изменить порядок интегрирования (сделать чертеж области).
2.Вычислить двойной
где область D, ограничена линиями
y = x .
где область D, ограничена линиями y = x,
y = 2x, x = 2, x = 3.
а)
б)
Слайд 24Список используемой литературы
1. Фихтенгольц Г.М. Курс дифференциального и интегрального исчисления. М.:
2. Кудрявцев Л.Д. Краткий курс математического анализа. М.: Наука, 2000.
3. Ильин В.А., Позняк Э.Г. Математический анализ. М.: Наука, 1999.
4. Смирнов В.И. Курс высшей математики.- Т.2. М.: Наука, 2005.