- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад на тему Презинтация по математику на тему Дифференциальная уравнения (студентов ВУЗа)
Содержание
- 1. Презинтация по математику на тему Дифференциальная уравнения (студентов ВУЗа)
- 2. План :Понятие о дифференциальном уравнении;Порядок дифференциального уравнения;Линейное
- 3. Альсеитов А. Карин Н.
- 4. Простейшие дифференциальные уравнения первого порядка.К
- 5. Решаем дифференциальное уравнение:Произведем нормировку уравнения. Разделим все уравнение на коэффициент при y'. Получим:
- 6. Слайд 6
- 7. Слайд 7
- 8. Слайд 8
- 9. Слайд 9
- 10. Слайд 10
- 11. Слайд 11
- 12. Слайд 12
- 13. Слайд 13
- 14. Слайд 14
- 15. Слайд 15
- 16. Слайд 16
- 17. Слайд 17
- 18. Слайд 18
- 19. Слайд 19
- 20. Слайд 20
- 21. Слайд 21
- 22. Слайд 22
- 23. Слайд 23
- 24. Слайд 24
- 25. Слайд 25
- 26. Слайд 26
- 27. Слайд 27
- 28. Слайд 28
- 29. Слайд 29
- 30. Слайд 30
- 31. ТЕОРЕМА КОШИ(о существовании и единственности решения ДУ)
- 32. Слайд 32
- 33. Слайд 33
- 34. Слайд 34
- 35. Слайд 35
- 36. Слайд 36
- 37. Слайд 37
- 38. Слайд 38
- 39. Слайд 39
- 40. Слайд 40
- 41. Слайд 41
- 42. Вопросы:1. Основные понятия. Геометрический смысл уравнения 1-го
План :Понятие о дифференциальном уравнении;Порядок дифференциального уравнения;Линейное дифференциальное уравнение;Однородное дифференциальное уравнение;Решение дифференциального уравнения;Общее и частное решение;Постановка задачи Коши.
Слайд 2План :
Понятие о дифференциальном уравнении;
Порядок дифференциального уравнения;
Линейное дифференциальное уравнение;
Однородное дифференциальное уравнение;
Решение
дифференциального уравнения;
Общее и частное решение;
Постановка задачи Коши.
Общее и частное решение;
Постановка задачи Коши.
Слайд 4 Простейшие дифференциальные уравнения первого порядка.
К ним относят:
1. Простейшие дифференциальные
уравнения первого порядка:
y’ =f(x) ;
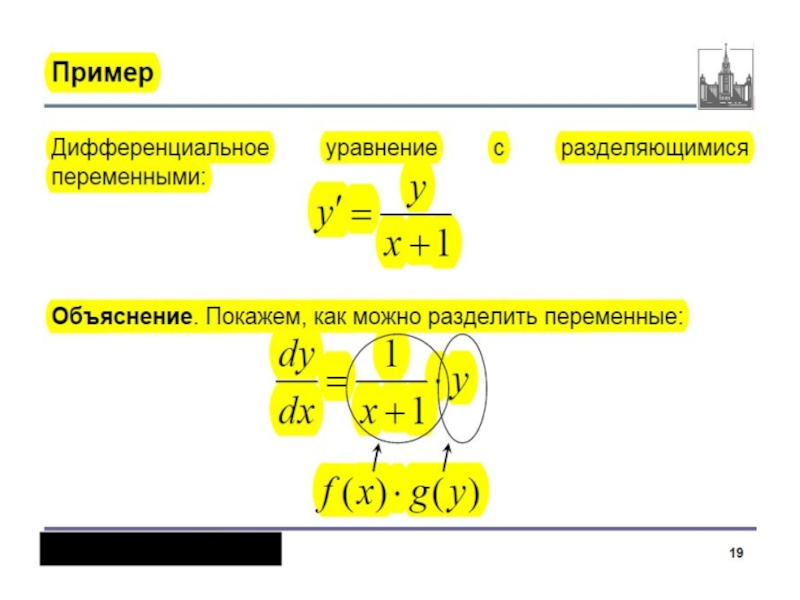
2. Уравнения с разделяющимися переменными:
y’= f (y / x) ;
3. Однородные уравнения первого порядка:
4. Линейные дифференциальные уравнения первого порядка:
y’+a (x) y= f (x) ;
f(x, y)= p(x) h(y) ;
Слайд 5Решаем дифференциальное уравнение:
Произведем нормировку уравнения. Разделим все уравнение на коэффициент при
y'. Получим:
Слайд 31
ТЕОРЕМА КОШИ
(о существовании и единственности решения ДУ)
Пусть дано ДУ
Если функция f(x,y) и ее частная производная f‘y(x,y) непрерывны в некоторой области D плоскости x,0,y, то в некоторой окрестности любой внутренней точки (х0,у0) этой области существует единственное решение этого уравнения, удовлетворяющего условию х=х0, у=у0.
Если функция f(x,y) и ее частная производная f‘y(x,y) непрерывны в некоторой области D плоскости x,0,y, то в некоторой окрестности любой внутренней точки (х0,у0) этой области существует единственное решение этого уравнения, удовлетворяющего условию х=х0, у=у0.
Слайд 42Вопросы:
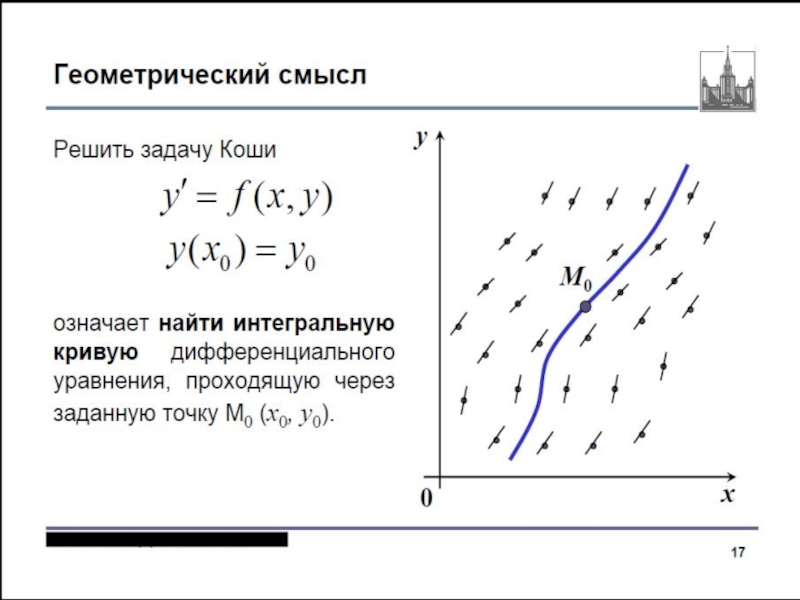
1. Основные понятия. Геометрический смысл уравнения 1-го порядка.
2. Уравнения с разделяющимися
переменными и приводящиеся к ним.
3. Линейные уравнения и приводящиеся к ним.
4. Уравнения в полных дифференциалах.
5. Системы дифференциальных уравнений в нормальной форме. Векторная запись. Задача Коши.
3. Линейные уравнения и приводящиеся к ним.
4. Уравнения в полных дифференциалах.
5. Системы дифференциальных уравнений в нормальной форме. Векторная запись. Задача Коши.