Разработано преподавателем математики: Фроловой Т.А.
- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад о математике Иррациональные уравнения
Содержание
- 1. Презентацияпо математике Иррациональные уравнения
- 2. «Мне приходится делить время между
- 3. Различные способы решенияИррациональные уравнения
- 4. Решение иррациональных уравнений Теоремы равносильности
- 5. Решение иррациональных уравненийТеоремы равносильности2. Если к обеим
- 6. Решение иррациональных уравнений 3.Если обе
- 7. Решение иррациональных уравненийПричина появления посторонних корнейУравнение (б)
- 8. Решение иррациональных уравненийУстная работаx= 2.5x=7x=3; x= x=3; x= -3x=3; x= 1Нет решенияОтвет: 1
- 9. Вид 1. Решение иррациональных уравнений.
- 10. Вид 2. Решение иррациональных уравненийДанное
- 11. Вид3 . Решение иррациональных уравнений. Пример 4.Это уравнение равносильно системе:Ответ: -1; -0,5.
- 12. Вид3. Решение иррациональных уравненийПример 5.
- 13. Вид4. Решение иррациональных уравненийПример 6.ОДЗ:Ответ: x=3.
- 14. Вид4. Решение иррациональных уравненийПреобразуем уравнение:
- 15. Решение иррациональных уравнений Вид5. Метод домножения на
- 16. Решение иррациональных уравнений Вид6. Уравнения, содержащие
- 17. Решение иррациональных уравнений Вид7. Уравнения вида Это
- 18. Решение иррациональных уравнений Пусть получим уравнение Получим
- 19. Решение иррациональных уравнений Замечаем, что, если тогда
- 20. Решение иррациональных уравнений Уравнения решаются заменойПоложимПодставим в уравнение, получим: u - v = 1.Получим систему:x=2; x=3.Ответ:Вид8.Пример11.
- 21. Решение иррациональных уравнений Уравнения решаются заменойПреобразуем уравнение: Пусть тогда получим: Ответ: 25.Пример12.ОДЗ:Вид8.
- 22. Решение иррациональных уравненийОДЗ:.Возведем обе части уравнения в
- 23. Решение иррациональных уравненийВозведем обе части уравнения в куб получим: По условию: Ответ: -5; -5,5; -6.Пример14.
- 24. Решение иррациональных уравнений Ответ: -2
- 25. Решение иррациональных уравнений1. . Домашнее задание1.7.2.3.4.5.6.8.9.10.
- 26. Решение иррациональных уравнений 1)1;3 2)4
Слайд 1Иррациональные уравнения
Дисциплина «Математика»
Раздел 2.
ЧАСТЬ 3.
Действительные числа
Тема 2.2. Уравнения и неравенства
Слайд 2 «Мне приходится делить время между политикой и уравнениями. Однако, уравнения,
Слайд 4Решение иррациональных уравнений
Теоремы равносильности
1.Если любое выражение, входящее
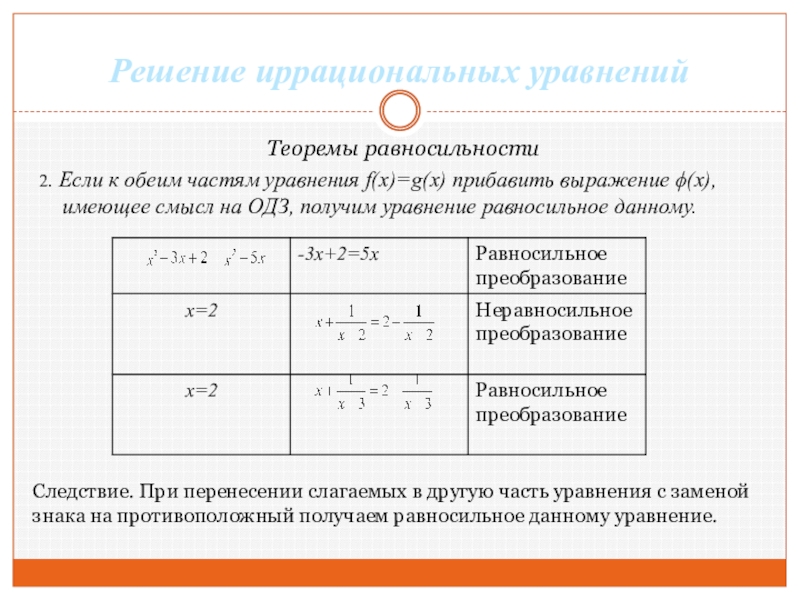
Слайд 5Решение иррациональных уравнений
Теоремы равносильности
2. Если к обеим частям уравнения f(x)=g(x) прибавить
Следствие. При перенесении слагаемых в другую часть уравнения с заменой знака на противоположный получаем равносильное данному уравнение.
Слайд 6Решение иррациональных уравнений
3.Если обе части уравнения умножить (разделить)
Слайд 7Решение иррациональных уравнений
Причина появления посторонних корней
Уравнение (б) совокупности (3) постороннее для
При возведении в квадрат (любую четную степень) возможно появление посторонних корней, наличие которых устанавливается, например, проверкой.
Слайд 8Решение иррациональных уравнений
Устная работа
x= 2.5
x=7
x=3; x=
x=3; x= -3
x=3; x=
Нет решения
Ответ: 1
Слайд 10
Вид 2. Решение иррациональных уравнений
Данное уравнение равносильно системе:
Ответ: 3.
Пример 2.
.
Пример3.
Преобразуем уравнение:
.
Полученное уравнение равносильно системе:
Ответ: -1.
Слайд 11
Вид3 . Решение иррациональных уравнений
.
Пример 4.
Это уравнение равносильно системе:
Ответ:
Слайд 14
Вид4. Решение иррациональных уравнений
Преобразуем уравнение:
Возведем обе части уравнения в
Полученное уравнение равносильно системе
Ответ: -2.
Пример 6
ОДЗ:
Слайд 15Решение иррациональных уравнений
Вид5. Метод домножения на сопряженное
Пример 6.
Заметим, что x=1 -
Проверка корни подтверждает
Ответ:
Слайд 16Решение иррациональных уравнений
Вид6. Уравнения, содержащие два и более радикала
.
Область
допустимых значений
Преобразуем уравнение:
Возведем обе части полученного уравнения в квадрат:
Это уравнение равносильно смешанной системе:
.
Ответ:
Пример7.
ОДЗ:
Слайд 17Решение иррациональных уравнений
Вид7. Уравнения вида
Это уравнение решается методом замены переменных.
тогда
получим систему:
.
Делаем обратную подстановку:
Пример8.
Ответ: x=68
Слайд 18Решение иррациональных уравнений
Пусть
получим уравнение
Получим совокупность двух уравнений:
Оба корня входят
Вид7. Уравнения вида
Пример10.
Ответ:
ОДЗ:
Слайд 19Решение иррациональных уравнений
Замечаем, что, если
тогда
являются взаимно обратными выражениями.
В
Пусть
получим:
Ответ: x=4
Пример9.
Вид7.Уравнения вида
Слайд 20Решение иррациональных уравнений
Уравнения решаются заменой
Положим
Подставим в уравнение, получим: u - v
Получим систему:
x=2; x=3.
Ответ:
Вид8.
Пример11.
Слайд 21Решение иррациональных уравнений
Уравнения решаются заменой
Преобразуем уравнение:
Пусть
тогда
получим:
Ответ: 25.
Пример12.
ОДЗ:
Вид8.
Слайд 22Решение иррациональных уравнений
ОДЗ:
.
Возведем обе части уравнения в куб
Из заданного неравенства вместо
в уравнение подставим ее
значение
Отсюда находим
2. Решим уравнение
Пример13.
Слайд 23Решение иррациональных уравнений
Возведем обе части уравнения в куб
получим:
По условию:
Ответ: -5; -5,5; -6.
Пример14.
Слайд 24Решение иррациональных уравнений
Ответ: -2
Ответ: 8
Ответ:
Ответ: 0
Ответ:5
Решите самостоятельно в тетради:
Слайд 26Решение иррациональных уравнений
1)1;3
2)4
3)5
4)4
6)-6
7)
Ответы к домашнему заданию:
8)-3;6
9)2
10)1