- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад аучные открытия Леонарда Эйлера
Содержание
- 1. ПрезентацияНаучные открытия Леонарда Эйлера
- 2. Биографические сведения о Леонардо ЭйлереИдеальный математик 18
- 3. стрельбы и таблицы движения Луны. Громадное наследие
- 4. В 26 лет Эйлер был избран российским
- 5. Вклад Эйлера в наукуЭйлер оставил важнейшие труды
- 6. механики, многочисленные приёмы интегрирования и решения дифференциальных
- 7. Теория чиселП. Л. Чебышёв писал: «Эйлером было
- 8. Слайд 8
- 9. Математический анализОдна из главных заслуг Эйлера перед
- 10. Слайд 10
- 11. тоже его заслуга, так же как их
- 12. ГеометрияВ элементарной геометрии Эйлер обнаружил несколько фактов,
- 13. Второй том «Введения в анализ бесконечно малых»
- 14. которая может быть наложена на плоскость без
- 15. КомбинаторикаЭйлер много внимания уделял представлению натуральных
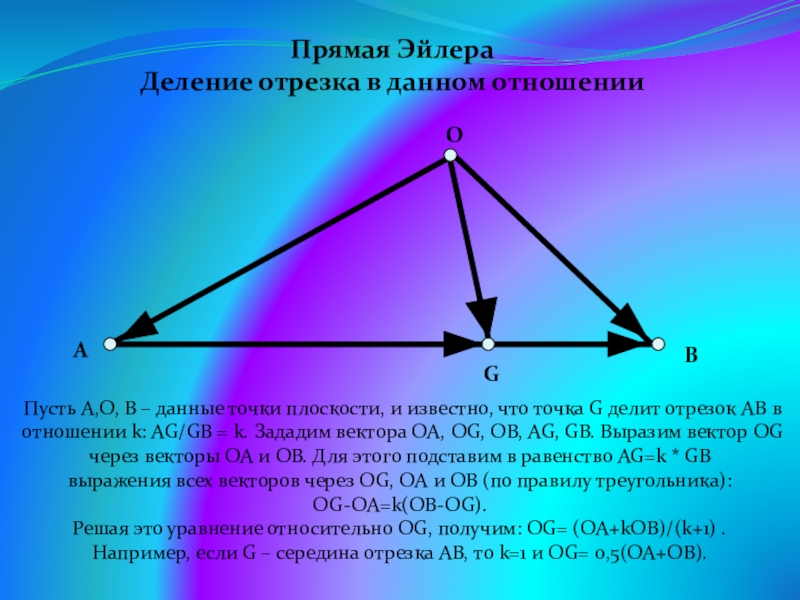
- 16. Прямая ЭйлераДеление отрезка в данном отношенииПусть A,О,
- 17. Прямая ЭйлераПрямая Эйлера – прямая, которой принадлежат
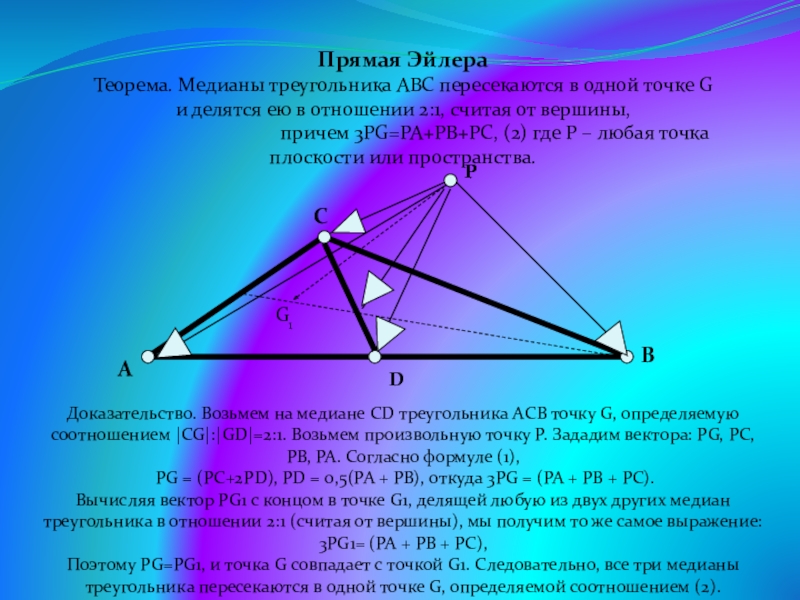
- 18. G1PПрямая ЭйлераТеорема. Медианы треугольника АВС пересекаются в
- 19. Теорема Эйлера о многогранникахИмеется много доказательств теоремы
- 20. Теорема Эйлера о многогранникахНекоторые следствия из теоремы1.
- 21. 2.Сумма плоских углов всех граней многогранника равна
- 22. граней, т.е. 2Р- ведь каждое из Р
- 23. Теория графов и задача ЭйлераИздавна среди жителей
- 24. В ходе рассуждений Эйлер пришёл к следующим
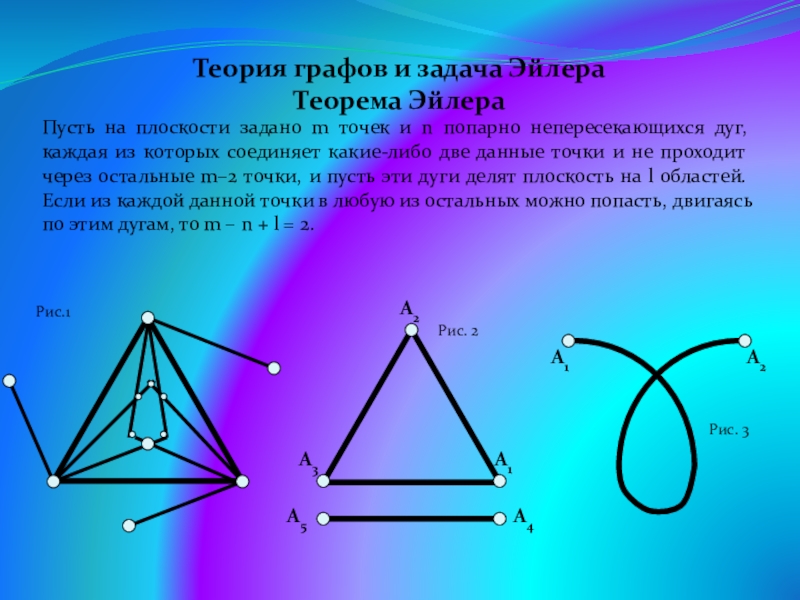
- 25. Теория графов и задача ЭйлераТеорема ЭйлераПусть на
- 26. В случае, изображенном на рисунке 1, все условия
- 27. ЗаключениеЭйлер оставил важнейшие труды по самым различным
- 28. Кроме математики, Эйлер занимался также многими другими,
- 29. Слайд 29
Слайд 1Научные открытия Леонарда Эйлера
В том усомниться
мог ли кто-то,
Что Эйлер
Что только цифры и расчеты
Его единственный кумир.
Выполнила: Алексина И.С.
Слайд 2Биографические сведения о Леонардо Эйлере
Идеальный математик 18 века - так часто
Слайд 3стрельбы и таблицы движения Луны.
Громадное наследие Эйлера включает 72 тома,
Заметим также, что вот уже в течение 300 лет школьники всего мира изучают математику, основы которой с ее новой символикой изложил в своих трудах тоже Леонард Эйлер.
Слайд 4В 26 лет Эйлер был избран российским академиком, но через 8
В начале сентября 1783 Эйлер почувствовал легкое недомогание. 18 сентября он еще занимался математическими исследованиями, но неожиданно потерял сознание и «прекратил вычислять и жить».
Слайд 5Вклад Эйлера в науку
Эйлер оставил важнейшие труды по самым различным отраслям
Благодаря Эйлеру в математику вошли общая теория рядов, удивительная по красоте «формула Эйлера», операция сравнения по целому модулю, полная теория непрерывных дробей, аналитический фундамент
Слайд 6механики, многочисленные приёмы интегрирования и решения дифференциальных уравнений, число e ,
Эйлер охотно участвовал в научных дискуссиях, из которых наибольшую известность получили:
спор о струне;
спор с Д'Аламбером о свойствах комплексного логарифма;
спор с английским оптиком Джоном Доллондом (англ.) о том, возможно ли создать ахроматическую линзу.
Во всех упомянутых случаях Эйлер отстаивал правильную позицию.
Слайд 7Теория чисел
П. Л. Чебышёв писал: «Эйлером было положено начало всех изысканий,
Эйлер продолжил исследования Ферма, ранее высказавшего (под влиянием Диофанта) ряд разрозненных гипотез о натуральных числах. Эйлер строго доказал эти гипотезы, значительно обобщил их и объединил их в содержательную теорию чисел. Он ввёл в математику исключительно важную «функцию Эйлера» и сформулировал с её помощью «теорему Эйлера». Эйлер создал теорию сравнений и квадратичных вычетов, указав для последних критерий
Слайд 9Математический анализ
Одна из главных заслуг Эйлера перед наукой — монография «Введение
Основание натуральных логарифмов было известно ещё со времён Непера и Якоба Бернулли, однако Эйлер дал настолько глубокое исследование этой важнейшей
Слайд 11тоже его заслуга, так же как их символика и обобщение на
Он первый дал систематическую теорию интегрирования и используемых там технических приёмов, нашёл важные классы интегрируемых дифференциальных уравнений. Он открыл эйлеровы интегралы — ценные классы специальных функций, возникающие при интегрировании: бета-функция и гамма-функция Эйлера.
Одновременно с Клеро вывел условия интегрируемости линейных дифференциальных форм от двух или трёх переменных (1739). Первый ввёл двойные интегралы. Получил серьёзные результаты в теории эллиптических функций, в том числе первые теоремы сложения.
Слайд 12Геометрия
В элементарной геометрии Эйлер обнаружил несколько фактов, не замеченных Евклидом:
три высоты
в треугольнике ортоцентр, центр описанной окружности и центр тяжести лежат на одной прямой — «прямой Эйлера»;
основания трёх высот произвольного треугольника, середины трёх его сторон и середины трёх отрезков, соединяющих его вершины с ортоцентром, лежат все на одной окружности (окружности Эйлера);
число вершин (В), граней (Г) и рёбер (Р) у любого выпуклого многогранника связаны простой формулой: В + Г = Р + 2.
Слайд 13Второй том «Введения в анализ бесконечно малых» (1748) — это первый
В 1760 году вышли фундаментальные «Исследования о кривизне поверхностей». Эйлер обнаружил, что в каждой точке гладкой поверхности имеются два нормальных сечения с минимальным и максимальным радиусами кривизны и что плоскости их взаимно перпендикулярны. Вывел формулу связи кривизны сечения поверхности с главными кривизнами.
Слайд 14которая может быть наложена на плоскость без складок и разрывов. Эйлер,
В треугольнике ABC ортоцентр H, центр U описанной окружности и центроид S лежат на одной «прямой Эйлера»
В 1771 году Эйлер опубликовал сочинение «О телах, поверхность которых можно развернуть на плоскость». В этой работе введено понятие развёртывающейся поверхности, то есть поверхности,
Слайд 15 Комбинаторика
Эйлер много внимания уделял представлению натуральных чисел в виде сумм
При решении комбинаторных задач он глубоко изучил свойства сочетаний и перестановок, ввёл в рассмотрение числа Эйлера.
Эйлер исследовал алгоритмы построения магических квадратов методом обхода шахматным конём. Две его работы (1776, 1779) заложили фундамент общей теории латинских и греко-латинских квадратов, огромная практическая ценность которой выяснилась после создания Рональдом Фишером методов планирования эксперимента, а также в теории кодов, исправляющих ошибки.
Слайд 16Прямая Эйлера
Деление отрезка в данном отношении
Пусть A,О, В – данные точки
выражения всех векторов через OG, OA и OB (по правилу треугольника): OG-OA=k(OB-OG).
Решая это уравнение относительно OG, получим: OG= (OA+kOB)/(k+1) .
Например, если G – середина отрезка AB, то k=1 и OG= 0,5(OA+OB).
Слайд 17Прямая Эйлера
Прямая Эйлера – прямая, которой принадлежат ортоцентр (точка пересечения высот)
Дан прямоугольный треугольник АСВ. Проведем медиану СО. Середина O гипотенузы AB является центром описанной около него окружности. Центроид G делит медиану CO в отношении 2:1, считая от вершины C. Катеты AC и BC являются высотами треугольника, поэтому вершина C прямого угла совпадает с ортоцентром H треугольника. Таким образом, точки O,G,H лежат на одной прямой, причем OH=3OG.
= Н
Слайд 18G1
P
Прямая Эйлера
Теорема. Медианы треугольника АВС пересекаются в одной точке G
и
причем 3PG=PA+PB+PC, (2) где P – любая точка плоскости или пространства.
Доказательство. Возьмем на медиане CD треугольника AСВ точку G, определяемую соотношением |CG|:|GD|=2:1. Возьмем произвольную точку P. Зададим вектора: PG, PC, PB, PA. Согласно формуле (1),
PG = (РС+2РD), PD = 0,5(PA + PB), откуда 3PG = (PA + PB + PC).
Вычисляя вектор PG1 с концом в точке G1, делящей любую из двух других медиан треугольника в отношении 2:1 (считая от вершины), мы получим то же самое выражение: 3PG1= (PA + PB + PC),
Поэтому PG=PG1, и точка G совпадает с точкой G1. Следовательно, все три медианы треугольника пересекаются в одной точке G, определяемой соотношением (2).
Слайд 19Теорема Эйлера о многогранниках
Имеется много доказательств теоремы Эйлера. В одной из
Слайд 20Теорема Эйлера о многогранниках
Некоторые следствия из теоремы
1. Р + 6≤ 3В
Доказательство:
Перепишем соотношение Эйлера дважды, один раз в виде
Р + 2 = В + Г
И другой раз в виде
4 = 2В - 2Р + 2Г
Складывая эти равенства, получаем
Р + 6 = 3В + 3Г - 2Р
Так как у каждой грани многогранника не менее трех сторон, то 3Г≤ 2Р. Отсюда сразу получаем Р + 6≤ 3В.
Утверждение доказано.
Слайд 212.Сумма плоских углов всех граней
многогранника равна 2πВ- 4π. (Теорема Декарта)
Доказательство:
Обозначим через Гi число i-угольных граней в многограннике М. Ясно, что
Г = Г3 + Г4 + Г5 + …
Ясно также, что каждая i-угольная грань содержит i ребер многогранника. С другой стороны, каждое ребро многогранника принадлежит в точности двум граням. Поэтому в сумме 3Г3 + 4Г4 + 5Г5 + … каждое ребро многогранника подсчитано, причем подсчитано дважды. Отсюда имеем
2Р = 3Г3 + 4Г4 + 5Г5 +…
Рассмотрим теперь сумму S плоских углов многогранника:
S = Г3 ·π + Г4 · 2π + Гi · ( i -2 )π + …
С учетом полученных соотношений и теоремы Эйлера соотношение можно переписать так:
S = Г3 ( 3 - 2 )π + Г4 (4 -2 )π + Гi ( i - 2 )π + … = 2Рπ - 2Гπ = 2Вπ - 4π.
Слайд 22граней, т.е. 2Р- ведь каждое из Р рёбер принадлежит двум граням.
Слайд 23Теория графов и задача Эйлера
Издавна среди жителей Кёнигсберга была распространена такая
В 1736 году задача о семи мостах заинтересовала выдающегося математика, члена Петербургской академии наук
Леонарда Эйлера, Эйлер пишет о том, что он смог найти правило, пользуясь которым легко определить есть ли у неё решение.
На упрощённой схеме части города (графе) мостам соответствуют линии (рёбра графа), а частям города — точки соединения линий (вершины графа).
Слайд 24В ходе рассуждений Эйлер пришёл к следующим выводам:
Число нечётных вершин (вершин,
Если все вершины графа чётные, то можно, не отрывая карандаша от бумаги, начертить граф, при этом можно начинать с любой вершины графа и завершить его в той же вершине.
Граф с более чем двумя нечётными вершинами невозможно начертить одним росчерком.
Граф кёнигсбергских мостов имел четыре нечётные вершины, следовательно невозможно пройти по всем мостам, не проходя ни по одному из них дважды.
Слайд 25Теория графов и задача Эйлера
Теорема Эйлера
Пусть на плоскости задано m точек
Слайд 26В случае, изображенном на рисунке 1, все условия теоремы Эйлера выполнены, m=12,
Слайд 27Заключение
Эйлер оставил важнейшие труды по самым различным отраслям математики, механики, физики,
Эйлер отличался несравненной работоспособностью и за свою жизнь написал около 900 научных работ, и это несмотря на то, что он потерял один глаз в возрасте 31 года и почти ослеп на второй в 66 лет. Нет ученого, имя которого упоминалось бы в учебной математической литературе столь же часто, как имя Эйлера. В учебниках для высшей школы их еще больше, а многие введенные им в обиход теоремы и методы давно перестали связывать с чьим-либо именем. Даже в средней школе логарифмы и тригонометрию изучают до сих пор в значительной степени «по Эйлеру».
Слайд 28Кроме математики, Эйлер занимался также многими другими, в том числе и
Полное собрание сочинений Эйлера рассчитано на 72 тома (вышло уже 62 больших тома). 30 из них посвящено математике, 31 содержит его работы по механике и. астрономии. 11 будут содержать работы по физике и другим предметам. В процентном отношении работы по математике распределяются (по объемам, а это дает лучшую характеристику, чем по числу работ, так как работы чрезвычайно отличаются по размерам) так: анализ — 60%, геометрия — 17%, теория чисел — 13%, алгебра — 7%, теория вероятностей — 3 %. Внутри анализа особенно большое место занимают работы по интегральному исчислению — 33 %; дифференциальным уравнениям посвящено 25%, рядам — 22% и вариационному исчислению —11%. В остальные 9% входят том «Дифференциальные исчисления» и первый том «Введения в анализ бесконечно малых».