- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад занятия по математике на тему Тригонометрические функции числового аргумента (1 курс СПО)
Содержание
- 1. Презентация занятия по математике на тему Тригонометрические функции числового аргумента (1 курс СПО)
- 2. План урокаОрганизационный моментПроверка домашнего заданияАктуализация знанийИзучение нового материалаПервичное закрепление материалаПроверочная работаРефлексияДифференцированное домашнее задание
- 3. Определение числовой функцииОпределение . Если даны числовое
- 4. Определение. Окружность
- 5. Движение по числовой окружности происходит
- 6. Если движение по числовой
- 7. Если точка М числовой окружности
- 8. 1)на 2 части
- 9. Тригонометрические функцииОпределение. Тригонометрические функции - это функции,
- 10. Определение. Если точка М числовой окружности
- 11. Слайд 11
- 12. Определение. Отношение синуса числа
- 13. Линия тангенсов
- 14. Определить синус и косинус углов по тригонометрическому кругу30°45°60°90°120°135°150°210°240°300°315°360°
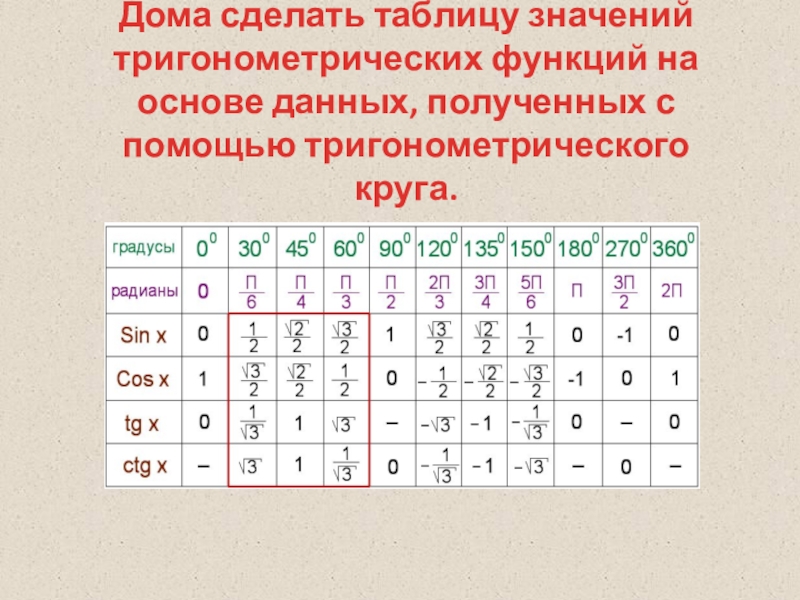
- 15. Дома сделать таблицу значений тригонометрических функций на основе данных, полученных с помощью тригонометрического круга.
- 16. Знаки косинуса Знаки синуса sin t Є
- 17. Работа с формулами №1.Дано: cos t=0,4; 90°
- 18. Решение заданий
- 19. 1 вариант
- 20. 1. Основные тригонометрические тождества
- 21. Домашнее заданиеНа оценку «3»-№ 7.17На оценку «4»-№ 7.17, 7.18На оценку «5»-№ 7.17, 7.18, 7.20
- 22. Подведение итоговЧто такое синус?Что такое косинус?Какое тождество
- 23. Наши результаты1.На уроке я работал 2.Своей работой
- 24. Спасибо за внимание!
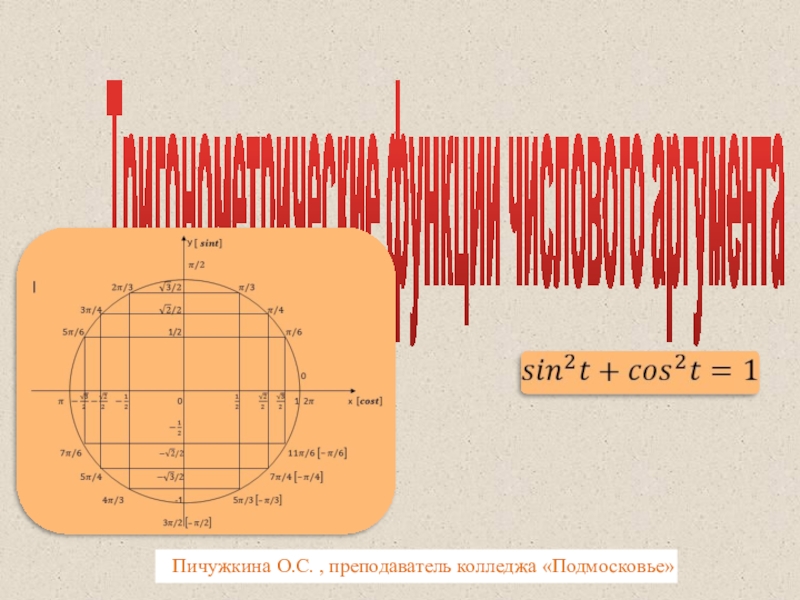
Слайд 1Тригонометрические функции числового аргумента
Пичужкина О.С. , преподаватель колледжа «Подмосковье»
Слайд 2План урока
Организационный момент
Проверка домашнего задания
Актуализация знаний
Изучение нового материала
Первичное закрепление материала
Проверочная работа
Рефлексия
Дифференцированное
Слайд 3Определение числовой функции
Определение . Если даны числовое множество X и правило
Для области определения функции используют обозначение D(f). Переменную x называют независимой переменной или аргументом, а переменную y – зависимой переменной. Множество всех значений функции y = f(x), x є X называют областью значений функции и обозначают E(f).
Слайд 4
Определение. Окружность называется единичной, если ее центр находится в
Уравнение числовой окружности:
x2 + y2 = 1
Тригонометрические функции
Числовая окружность
Слайд 5
Движение по числовой окружности происходит против часовой стрелки
π/2
π
3π/2
2π
I четверть
II
III четверть
IV четверть
Тригонометрические функции
Числовая окружность
Слайд 6
Если движение по числовой окружности происходит по часовой стрелке, то
-π/2
-π
-3π/2
-2π
Тригонометрические функции
Числовая окружность
Слайд 7
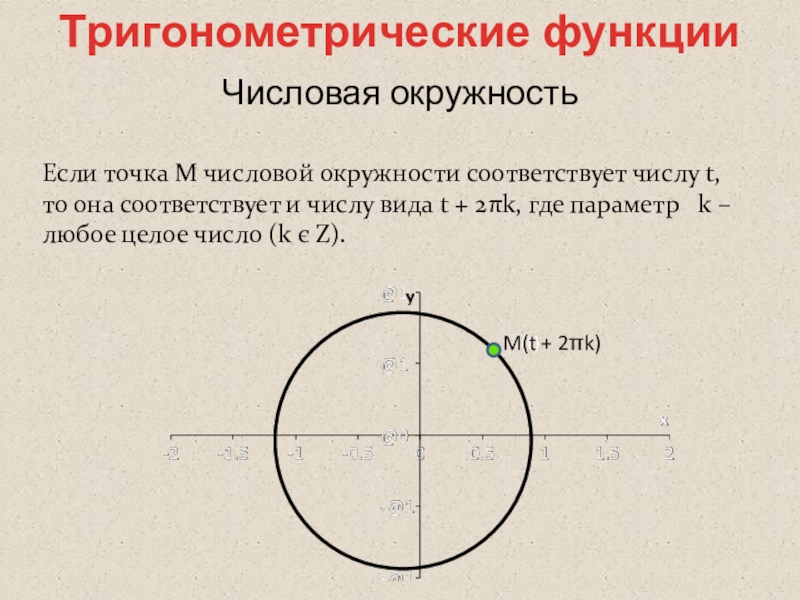
Если точка М числовой окружности соответствует числу t, то она
M(t)
M(t + 2πk)
Тригонометрические функции
Числовая окружность
Слайд 8 1)на 2 части
R K
В А В А В A AА
M N
D D
4)на 12 частей С 5)на 6 частей
O Z O Z Указать длины дуг: 2)AD
P F 3)AR, KM, ND, AM, NA
4)AO, AG, CB, CE, AT, AE, PE
B A B A 5)AZ, ZB, AB, ZH, OZ
G T
E H E H
D
Деление на части
Слайд 9Тригонометрические функции
Определение. Тригонометрические функции - это функции, устанавливающие зависимость между сторонами
Тригонометрические функции угла α определяются при помощи числовой окружности, а также из прямоугольного треугольника (для острых углов).
Слайд 10
Определение. Если точка М числовой окружности соответствует числу t, то
Если M(t) = M(x; y), то x = cos t, y = sin t.
M (t)
cos t
sin t
Тригонометрические функции
Синус и косинус
Слайд 11
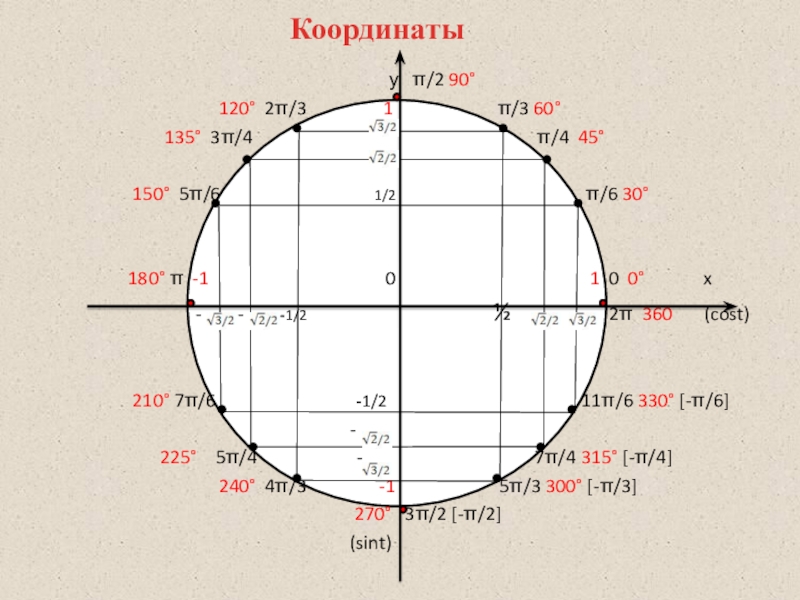
120° 2π/3 1 π/3 60°
135° 3π/4 π/4 45°
150° 5π/6 1/2 π/6 30°
180° π -1 0 1 0 0° x
- - -1/2 ½ 2π 360 (cost)
210° 7π/6 -1/2 11π/6 330° [-π/6]
-
225° 5π/4 - 7π/4 315° [-π/4]
240° 4π/3 -1 5π/3 300° [-π/3]
270° 3π/2 [-π/2]
(sint)
Координаты
Слайд 12
Определение. Отношение синуса числа t к косинусу того же числа
Определение. Отношение косинуса числа t к синусу того же числа называют котангенсом числа t и обозначают ctg t.
Тригонометрические функции
Тангенс и котангенс
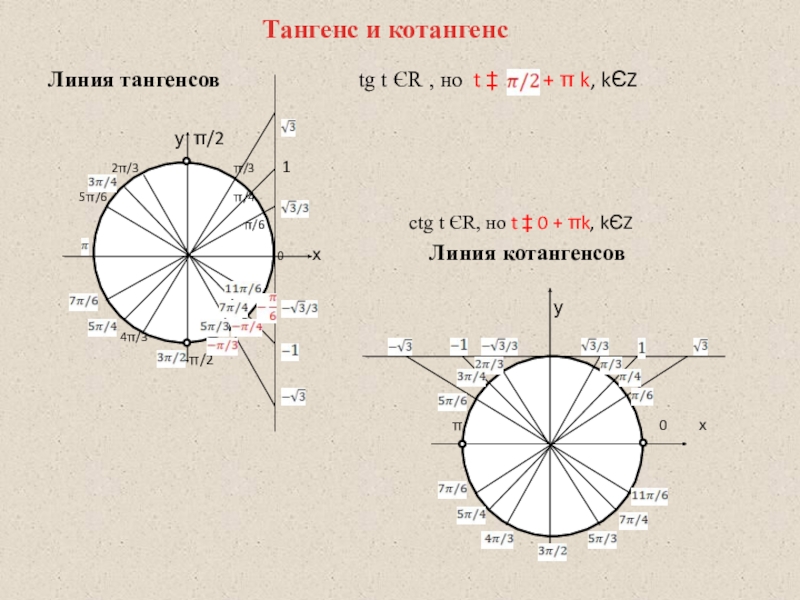
Слайд 13Линия тангенсов
у π/2
2π/3 π/3 1
5π/6 π/4
π/6 ctg t ЄR, но t ‡ 0 + πk, kЄZ
0 х Линия котангенсов
у
4π/3
-π/2
π 0 х
Тангенс и котангенс
Слайд 14Определить синус и косинус углов по тригонометрическому кругу
30°
45°
60°
90°
120°
135°
150°
210°
240°
300°
315°
360°
Слайд 15Дома сделать таблицу значений тригонометрических функций на основе данных, полученных с
Слайд 16 Знаки косинуса Знаки синуса
sin t Є [-1;1]
Знаки тангенса Знаки котангенса
tg t Є R ctg t Є R
Знаки и значения
Слайд 17Работа с формулами
№1.Дано: cos t=0,4; 90°
Решение:
1)sin²t + cos²t=1,
sin²t=1 - cos²t,
sin²t=1 - 0,16,
sin²t=0,84,
т.к. tЄ2ч, то sint>0
sin t=+
sin t =
Ответ: .
Слайд 191 вариант
1.На числовой окружности отметить числа(3 балла):
13π/6; - 1; 10π 9π/4; 2; -8π -5π/3; 3; 6π
2.Единичная окружность разбита на части(4 балла):
A K E A
F M K E
P T
D C D C D C
O N
S G R H R H
B B
Найдите длины следующих дуг:
CA, CS, CG, BD CE, CR, CH, HR CT, CP, CN, RD
3.Определить знак числа(5 баллов):
1) cos 95° 1) cos 280° 1) cos 190°
2) sin 7π/3 2) sin 11π/6 2) sin 13π/4
3) tg (-π/6) 3) tg (-π/4) 3) tg (-π/3)
Проверочная работа
Слайд 21Домашнее задание
На оценку «3»-№ 7.17
На оценку «4»-№ 7.17, 7.18
На оценку «5»-№
Слайд 22Подведение итогов
Что такое синус?
Что такое косинус?
Какое тождество связывает эти функции?
Что такое
Что такое котангенс?
Какое тождество связывает эти функции?
Слайд 23Наши результаты
1.На уроке я работал
2.Своей работой на уроке я
3.Урок
4.За урок я
5.Мое настроение
6.Материал урока мне был
7.Домашнее задание мне кажется
активно / пассивно
доволен / не доволен
коротким / длинным
не устал / устал
стало лучше / стало хуже
понятен / не понятен
полезен / бесполезен
интересен / скучен
легким / трудным
интересно / не интересно










![Презентация занятия по математике на тему Тригонометрические функции числового аргумента (1 курс СПО) Знаки косинуса Знаки синуса sin t Є [-1;1] Знаки косинуса Знаки синуса sin t Є [-1;1]](/img/thumbs/ac4db51ef766caaca11a2103d1c92144-800x.jpg)













