ЕВДОКИМОВА И.Г.
МОУ «СОШ № 75»
Г. САРАТОВ
- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад Загадки параболы
Содержание
- 1. Презентация Загадки параболы
- 2. ТЕМА ЗАНЯТИЯ ОПРЕДЕЛЕНИЕ ЗНАКОВ КОЭФФИЦИЕТОВ КВАДРАТНОГО
- 3. Какая функция называется квадратичной?Функция вида
- 4. Слайд 4
- 5. Графиком квадратичной функции является параболаНаправление ветвей параболыЕсли
- 6. Определить направление ветвей параболы
- 7. Кроме того,модуль коэффициента а отвечает за
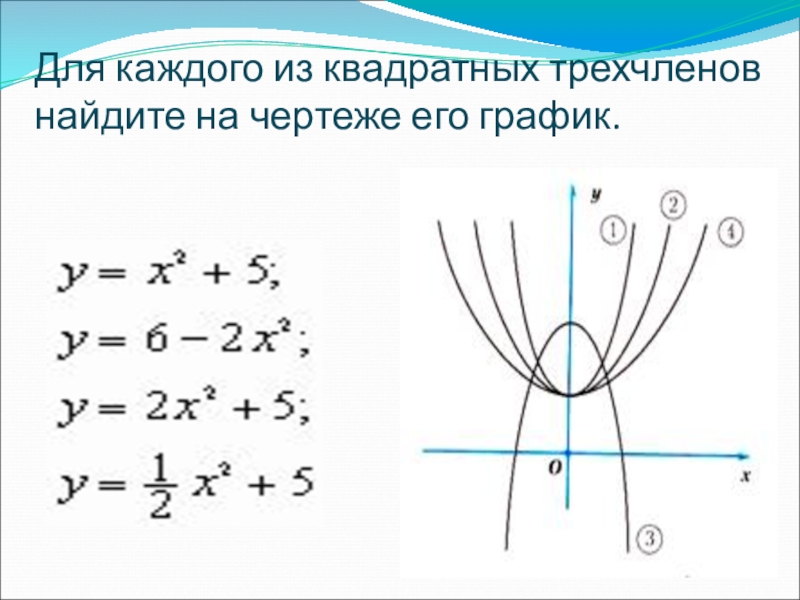
- 8. Для каждого из квадратных трехчленов найдите
- 9. a = …b = …c = …D
- 10. Знак дискриминанта D определяет количество корней квадратного
- 11. ОПРЕДЕЛЕНИЕ ЗНАКОВ КОРНЕЙ КВАДРАТНОГО ТРЁХЧЛЕНА
- 12. Слайд 12
- 13. ОПРЕДЕЛЕНИЕ ЗНАКОВ КОРНЕЙ КВАДРАТНОГО ТРЁХЧЛЕНА.На каком из
- 14. хууху0х00ухНа рисунках показаны графики некоторых функций у=aх2+bx+с. Укажите верную комбинацию. а0a>0, D0, D
- 15. КАК ПРОЧИТАТЬ НА ЧЕРТЕЖЕ ЗНАЧЕНИЕ КОЭФФИЦИЕНТА
- 16. Слайд 16
- 17. Слайд 17
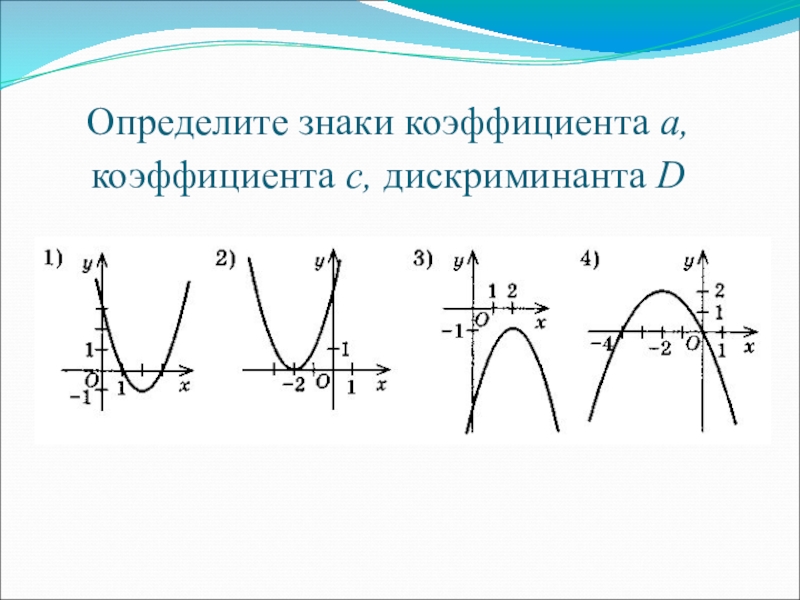
- 18. Определите знаки коэффициента а, коэффициента с, дискриминанта D
- 19. Дано: сопоставьте условия графику
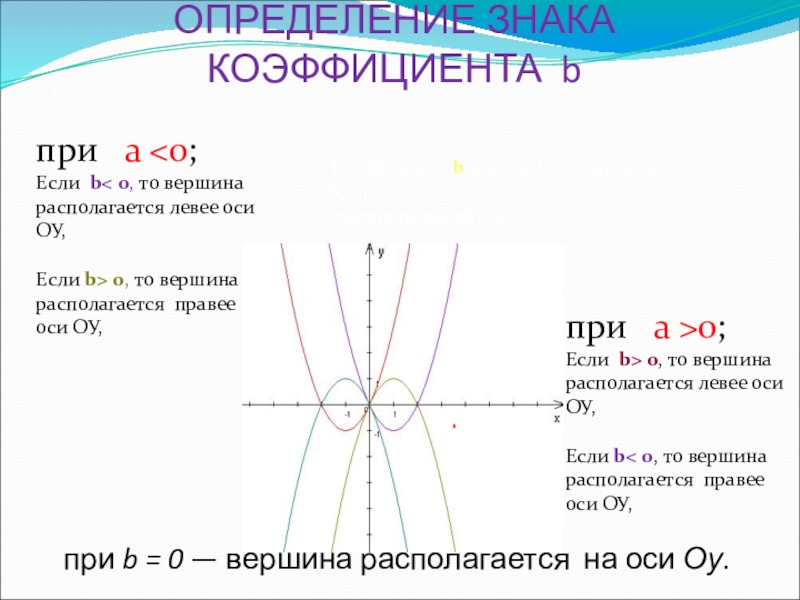
- 20. КАК РАСПОЛАГАЕТСЯ ВЕРШИНА ПАРАБОЛЫ ОТНОСИТЕЛЬНО ОСИ Коэффициент
- 21. ОПРЕДЕЛЕНИЕ ЗНАКА КОЭФФИЦИЕНТА bпри a 0,
- 22. По графику квадратичной функции определите знаки коэффициентов a, b, c. ха)
- 23. хуНа рисунке показан график некоторой функции у=aх2+bx+с.
- 24. хуНа рисунке показан график некоторой функции у=aх2+bx+с.
- 25. хуНа рисунке показан график некоторой функции у=aх2+bx+с. Укажите верную комбинацию. аb>0, D>0c>0, b0, D
- 26. Экзаменационные заданияГрафик какой из перечисленных ниже функций изображен на рисунке? 0-4
- 27. Экзаменационные задания
- 28. Слайд 28
- 29. --------------------------I I I
- 30. ЗадачаИзвестно, что парабола, являющаяся графиком квадратного трехчлена
- 31. Подведение итоговВО ВРЕМЯ НАШЕГО ЗАНЯТИЯ БЫЛА ПРОВЕДЕНА
- 32. ПРИ РЕШЕНИИ УПРАЖНЕНИЙ И ЗАДАЧ
- 33. Спасибо за урок!
ТЕМА ЗАНЯТИЯ ОПРЕДЕЛЕНИЕ ЗНАКОВ КОЭФФИЦИЕТОВ КВАДРАТНОГО ТРЁХЧЛЕНА ах2+bх+с И ЗНАКА ДИСКРИМИНАНТА D .
Слайд 1Загадки параболы
ЗАНЯТИЕ ПО ПОДГОТОВКЕ К ГОСУДАРСТВЕННОЙ ИТОГОВОЙ АТТЕСТАЦИИ В 9 КЛАССЕ
УЧИТЕЛЬ:
Слайд 2ТЕМА ЗАНЯТИЯ
ОПРЕДЕЛЕНИЕ ЗНАКОВ КОЭФФИЦИЕТОВ КВАДРАТНОГО ТРЁХЧЛЕНА
ах2+bх+с
И ЗНАКА
ДИСКРИМИНАНТА D .
Слайд 3Какая функция называется квадратичной?
Функция вида у = ах2+bх+с,
где а,
b, c – заданные числа, а≠0,
х – действительная переменная, называется квадратичной функцией.
Примеры:
1) у=5х+1 4) у=x3+7x-1
2) у=3х2-1 5) у=4х2
3) у=-2х2+х+3 6) у=-3х2+2х
х – действительная переменная, называется квадратичной функцией.
Примеры:
1) у=5х+1 4) у=x3+7x-1
2) у=3х2-1 5) у=4х2
3) у=-2х2+х+3 6) у=-3х2+2х
.
Слайд 4 ПОКАЖЕМ, КАК МОЖНО ПОЛУЧИТЬ МАССУ ИНФОРМАЦИИ О КОЭФФИЦИЕНТАХ КВАДРАТНОГО ТРЁХЧЛЕНА
ax²+bx+c, РАССМАТРИВАЯ ЕГО ГРАФИК- ПАРАБОЛУ.
РАССМАТРИВАЯ
ПАРАБОЛУ…
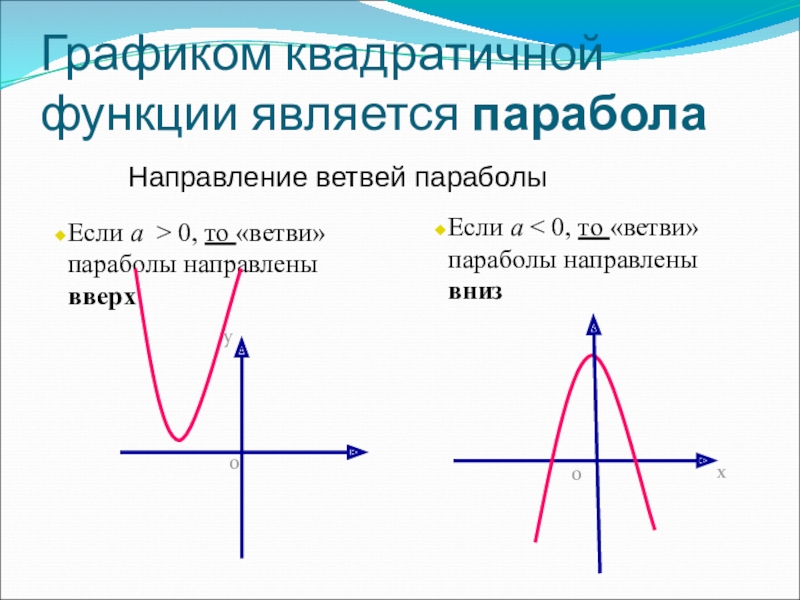
Слайд 5Графиком квадратичной функции является парабола
Направление ветвей параболы
Если а > 0, то
«ветви» параболы направлены вверх
Если а < 0, то «ветви» параболы направлены вниз
Слайд 7
Кроме того,
модуль коэффициента а отвечает за
«крутизну» параболы:
чем
больше |a|, тем «круче» парабола.
Слайд 9
a = …
b = …
c = …
D < 0
D = 0
D
> 0
действительных
корней
нет
Сколько корней может иметь квадратный трёхчлен, который задаёт кв. функцию?
Отчего зависит количество корней?
Слайд 10Знак дискриминанта D определяет количество корней квадратного трёхчлена.
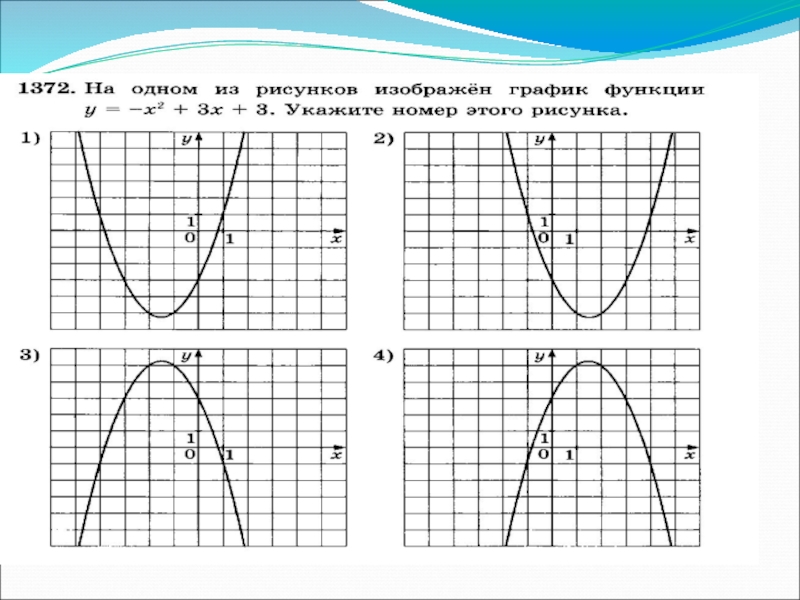
На рисунке изображен график
функции у = ах2 + bx + c. Используя рисунок, определите число корней квадратного трёхчлена ах2 + bx + c .
Слайд 12
ОПРЕДЕЛЕНИЕ ЗНАКОВ КОРНЕЙ КВАДРАТНОГО ТРЁХЧЛЕНА.
На каком из рисунков изображён график квадратичной
функции у=ах²+bх+с, если известно, что а<0 и квадратный
трёхчлен имеет корни разных знаков?
трёхчлен имеет корни разных знаков?
Слайд 13ОПРЕДЕЛЕНИЕ ЗНАКОВ КОРНЕЙ КВАДРАТНОГО ТРЁХЧЛЕНА.
На каком из рисунков изображён график квадратичной
функции у=ах²+bх+с, если известно, что а<0 и квадратный трёхчлен имеет отрицательные корни?
Слайд 14
х
у
у
х
у
0
х
0
0
у
х
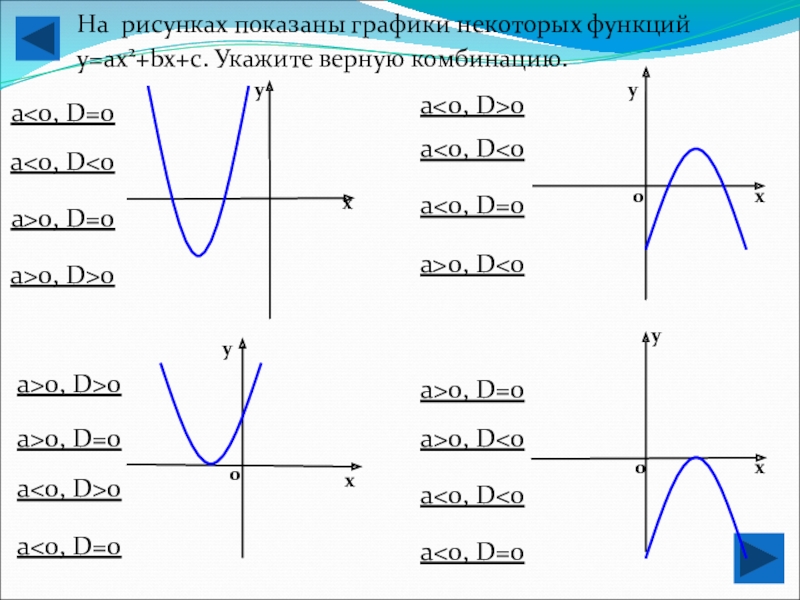
На рисунках показаны графики некоторых функций у=aх2+bx+с. Укажите верную комбинацию.
а
D=0
a<0, D<0
a>0, D=0
a>0, D>0
a>0, D<0
a<0, D<0
a<0, D=0
a<0, D>0
a>0, D>0
a<0, D=0
a<0, D>0
a>0, D=0
a>0, D=0
a>0, D<0
a<0, D<0
a<0, D=0
Слайд 15КАК ПРОЧИТАТЬ НА ЧЕРТЕЖЕ ЗНАЧЕНИЕ КОЭФФИЦИЕНТА с?
с = y (0)
—ордината точки пересечения параболы с осью Оу.
Слайд 19Дано: сопоставьте условия графику а) а > 0; D
> 0; c < 0;
б) а > 0; D = 0; c > 0;
в) а < 0; D < 0; c < 0;
г) а < 0; D > 0; c = 0;
д) а > 0; с = 0; D = 0.
Слайд 20КАК РАСПОЛАГАЕТСЯ ВЕРШИНА ПАРАБОЛЫ ОТНОСИТЕЛЬНО ОСИ
Коэффициент b ( вместе с
коэффициентом a)
определяет абсциссу вершины параболы.
1.Выразим коэффициент b.
2.Определим знак выражения
3. Поменяем знак выражения на противоположный и узнаем знак коэффициента b
определяет абсциссу вершины параболы.
1.Выразим коэффициент b.
2.Определим знак выражения
3. Поменяем знак выражения на противоположный и узнаем знак коэффициента b
Слайд 21ОПРЕДЕЛЕНИЕ ЗНАКА КОЭФФИЦИЕНТА b
при a
вершина располагается левее оси ОУ,
Если b> 0, то вершина располагается правее оси ОУ,
Если b> 0, то вершина располагается правее оси ОУ,
при a >0;
Если b> 0, то вершина располагается левее оси ОУ,
Если b< 0, то вершина располагается правее оси ОУ,
при b = 0 — вершина располагается на оси Оу.
) Коэффициент b(вместе с ) определяет абсциссу
вершины параболы:
Слайд 23
х
у
На рисунке показан график некоторой функции у=aх2+bx+с. Укажите верную комбинацию.
bD
cD>0
ac>0
ac<0,
D>0, т.к. ….
a<0, т. к. …
c>0, т. к. …
b>0, т. к. …
ПОМОЩЬ
ab>0
Слайд 24
х
у
На рисунке показан график некоторой функции у=aх2+bx+с. Укажите верную комбинацию.
аc>0
cD>0
ab0
bc>0
D>0,
т.к. ….
a>0, т. к. …
c<0, т. к. …
b>0, т. к. …
ПОМОЩЬ
Слайд 25
х
у
На рисунке показан график некоторой функции у=aх2+bx+с. Укажите верную комбинацию.
аb>0,
D>0
c>0, b<0
ab>0, D<0
ab<0, D<0
D<0, т.к. ….
a<0, т. к. …
c<0, т. к. …
b>0, т. к. …
ПОМОЩЬ
Слайд 29--
--
--
--
--
--
--
--
--
--
--
--
--
I I I I
I I I I I I
х
у
На рисунке показан график некоторой функции y=ax2+bx+c. Найдите формулу, задающую эту функцию.
у = –х2+4х –3
у = х2+4х –3.
у = –х2 –4х -3
у = –х2 – 4х +3
-5 -4 -3 -2 -1
1
-3
Слайд 30Задача
Известно, что парабола, являющаяся графиком квадратного трехчлена у
= ах² + 10х + с, не имеет точек в третьей четверти. Какое из следующих утверждений может быть неверным?
(A) а>0
(B) Вершина параболы лежит
во второй четверти.
(C) с ≥ 0
(D) c > 0,1
(Е) 10²– 4 ас ≤ 0.
(A) а>0
(B) Вершина параболы лежит
во второй четверти.
(C) с ≥ 0
(D) c > 0,1
(Е) 10²– 4 ас ≤ 0.
Слайд 31Подведение итогов
ВО ВРЕМЯ НАШЕГО ЗАНЯТИЯ БЫЛА ПРОВЕДЕНА САМОСТОЯТЕЛЬНАЯ РАБОТА.
МАКСИМАЛЬНОЕ КОЛИЧЕСТВО БАЛЛОВ
15
БАЛЛОВ.
ОЦЕНИТЕ,КАК ВЫ УСВОИЛИ МАТЕРИАЛ
«5» - 10-11 БАЛЛОВ
«4» - 8-9 БАЛЛОВ
«3» - 6-7 БАЛЛОВ
ОЦЕНИТЕ,КАК ВЫ УСВОИЛИ МАТЕРИАЛ
«5» - 10-11 БАЛЛОВ
«4» - 8-9 БАЛЛОВ
«3» - 6-7 БАЛЛОВ
Слайд 32
ПРИ РЕШЕНИИ УПРАЖНЕНИЙ И ЗАДАЧ МЫ ОСНОВЫВАЛИСЬ НА ТЕХ
ФАКТАХ, КОТОРЫЕ УЗНАЛИ О КОЭФФИЦИЕНТАХ КВАДРАТНОГО ТРЁХЧЛЕНА.
НА САМОМ ДЕЛЕ, СВОЙСТВА ПАРАБОЛЫ ЧРЕЗВЫЧАЙНО БОГАТЫ И РАЗНООБРАЗНЫ И ДАЛЬНЕЙШЕЕ ЗНАКОМСТВО С НИМИ МЫ ПРОДОЛЖИМ ПРИ НОВЫХ ВСТРЕЧАХ.
НА САМОМ ДЕЛЕ, СВОЙСТВА ПАРАБОЛЫ ЧРЕЗВЫЧАЙНО БОГАТЫ И РАЗНООБРАЗНЫ И ДАЛЬНЕЙШЕЕ ЗНАКОМСТВО С НИМИ МЫ ПРОДОЛЖИМ ПРИ НОВЫХ ВСТРЕЧАХ.
