- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад Взаимное расположение прямых на плоскости, используя приём классификация.
Содержание
- 1. Презентация Взаимное расположение прямых на плоскости, используя приём классификация.
- 2. Слайд 2
- 3. Слайд 3
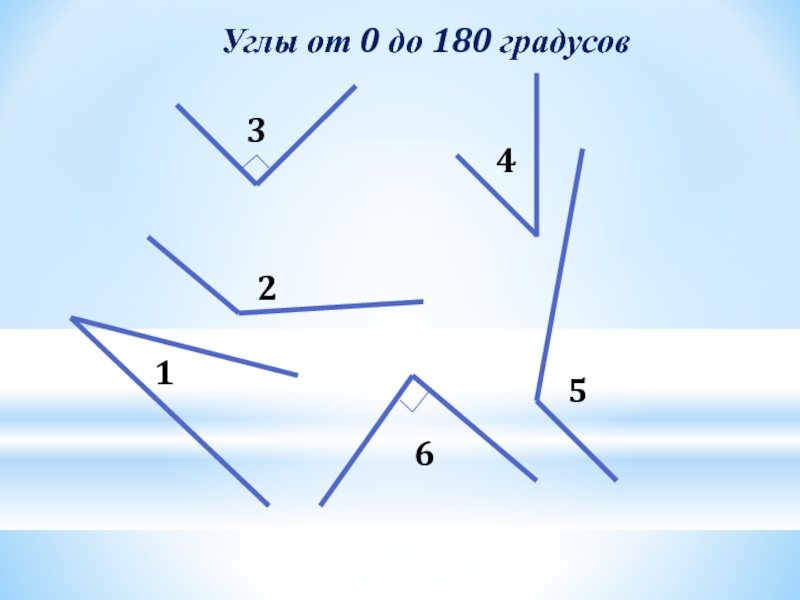
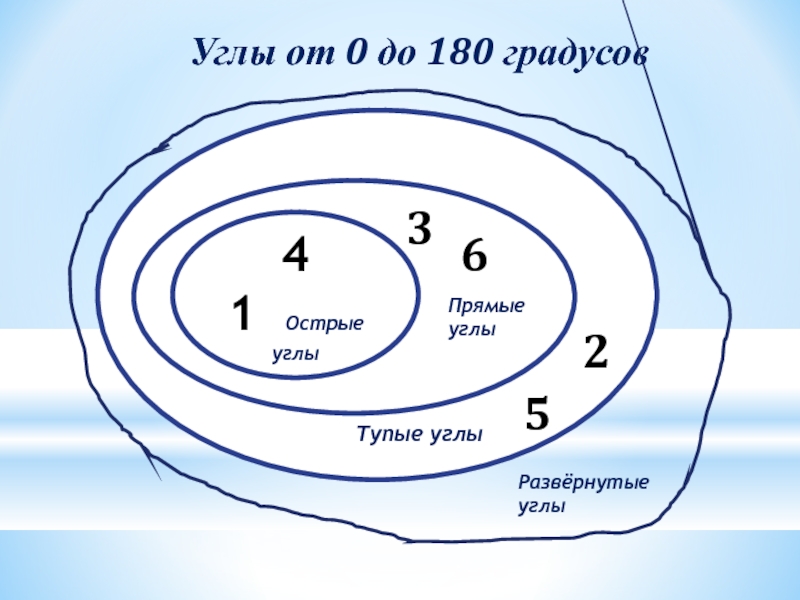
- 4. 123456Углы от 0 до 180 градусов
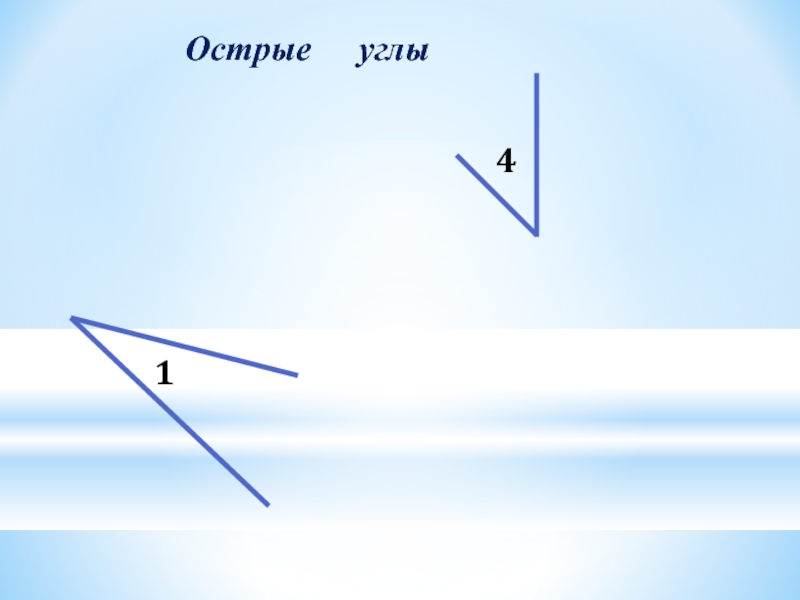
- 5. 14Острые углы
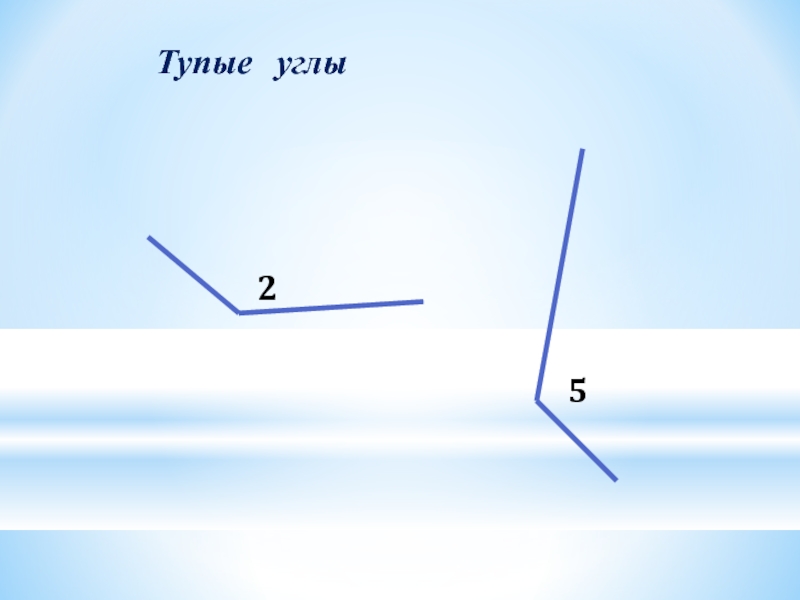
- 6. 25Тупые углы
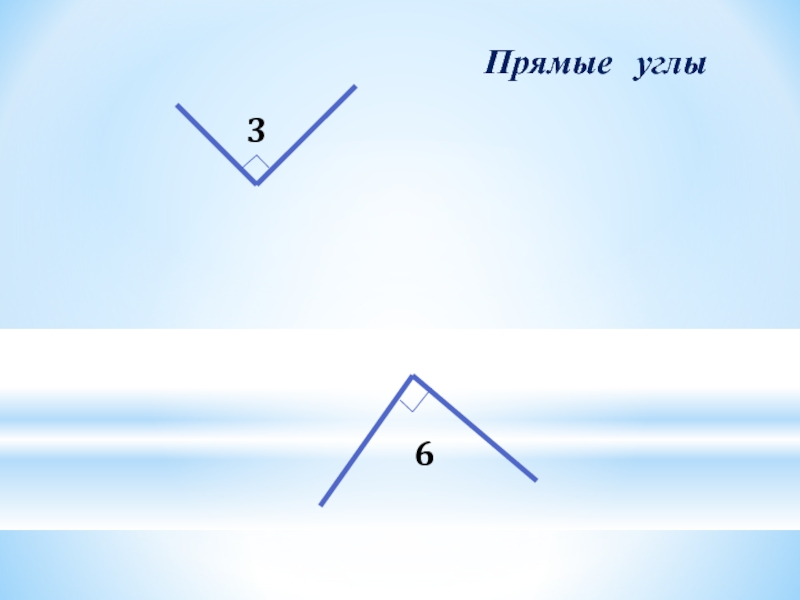
- 7. 36Прямые углы
- 8. 4 1 Острые углы6325Углы от 0 до 180 градусовПрямые углыТупые углыРазвёрнутые углы
- 9. Взаимное расположение прямых на плоскости
- 10. Параллельные прямыеПересекающиеся прямыеА
- 11. Построение параллельных прямых
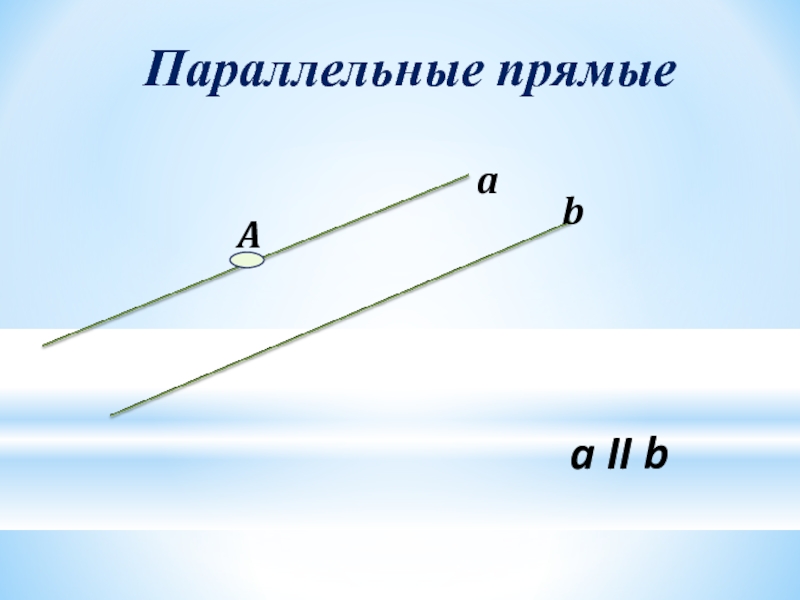
- 12. Параллельные прямыеa II b
- 13. «Параллельные прямые»Евкли́д или Эвкли́д (3 в. до н. э.) древнегреческий математик,
- 14. Никола́й Ива́нович Лобаче́вский — русский математик, создатель неевклидовой геометрии Лобачевский
- 15. Слайд 15
- 16. Слайд 16
- 17. Слайд 17
- 18. Слайд 18
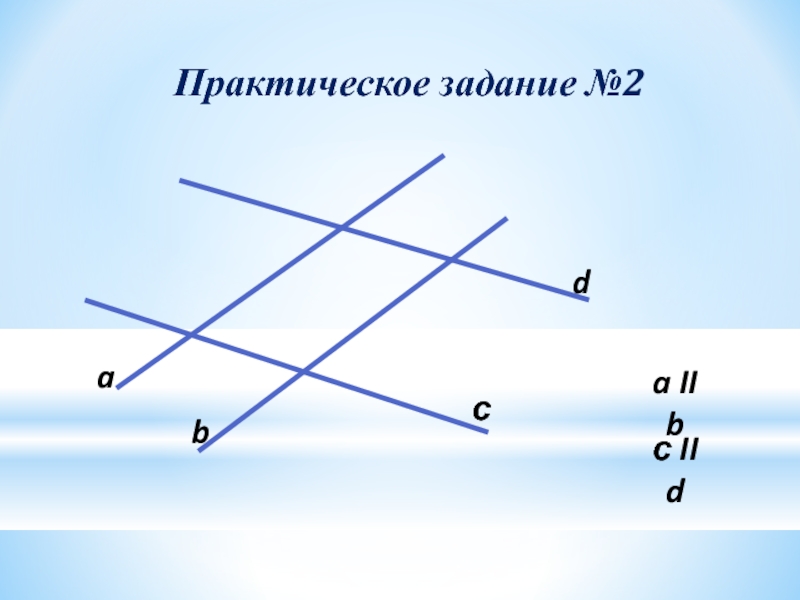
- 19. Практическое задание №2a II bс II dabсd
- 20. ПарфенонХрам Афины Парфенос в Афинах 447-438
- 21. Исаакиевский соборПостроен в 1818Построен в 1818—1858 годы по проекту архитектора Огюста
- 22. Казанский соборПостроен на Невском проспекте в 1801—1811 годах архитектором
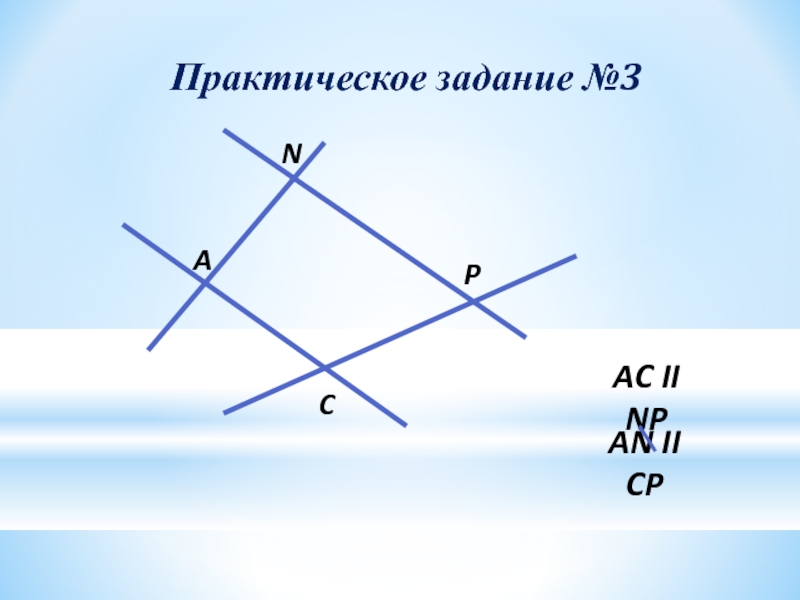
- 23. Практическое задание №3AC II NPAN II CPANPC
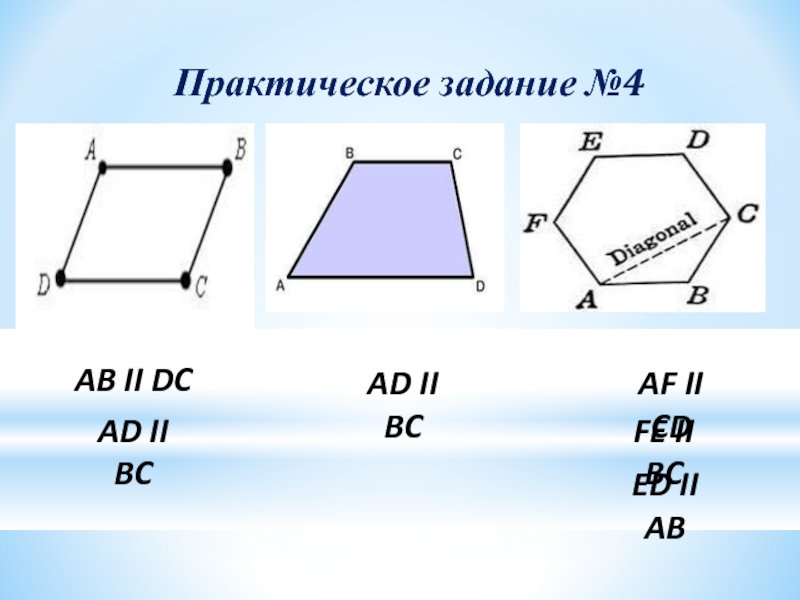
- 24. Практическое задание №4AD II BCAB II DCAD II BCAF II CDFE II BCED II AB
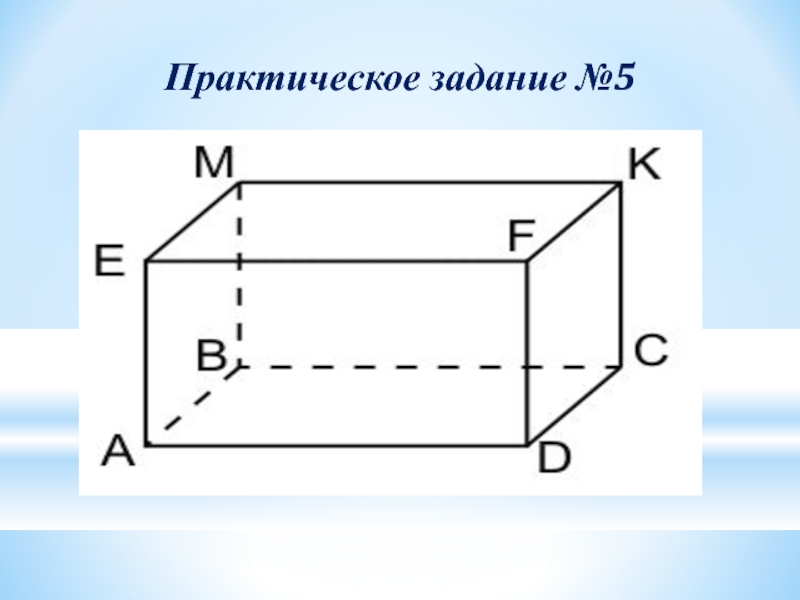
- 25. Практическое задание №5
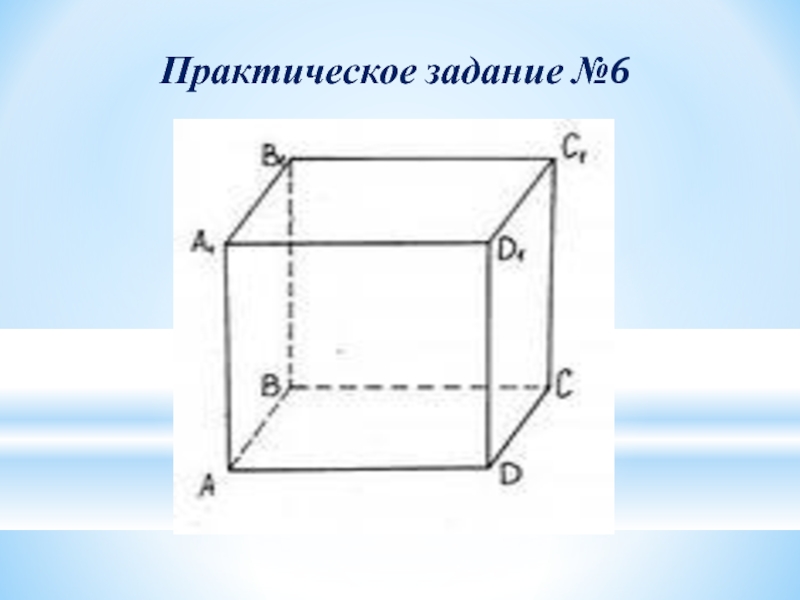
- 26. Практическое задание №6
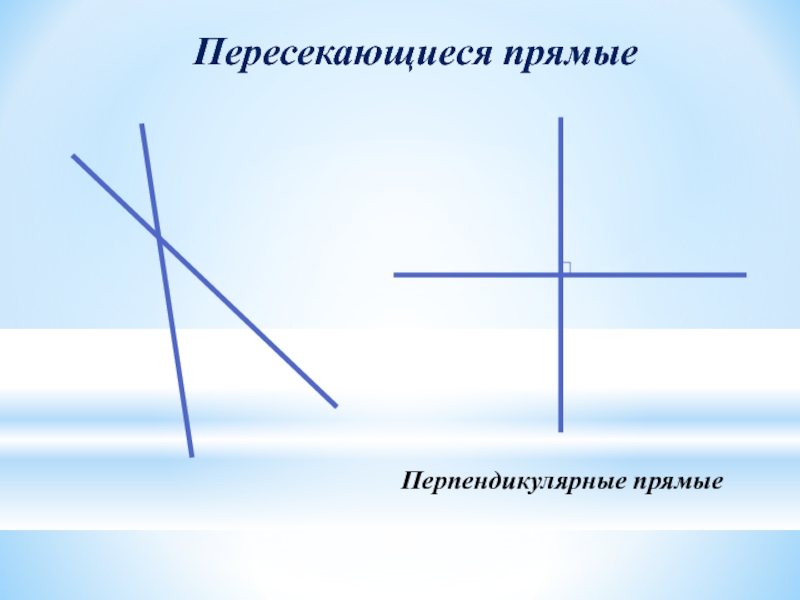
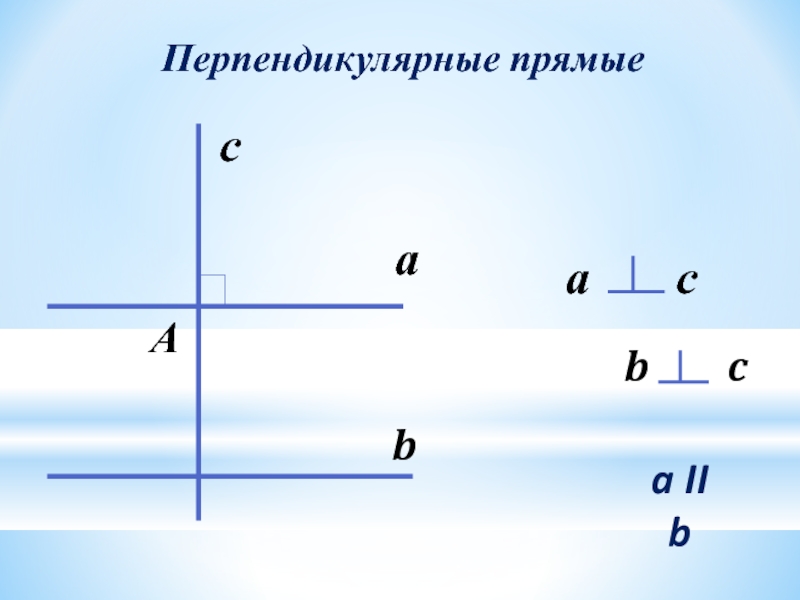
- 27. Пересекающиеся прямыеПерпендикулярные прямые
- 28. Перпендикулярные прямыеса а сb b ca II bА
- 29. Вывод:Два перпендикуляра к одной прямой параллельны
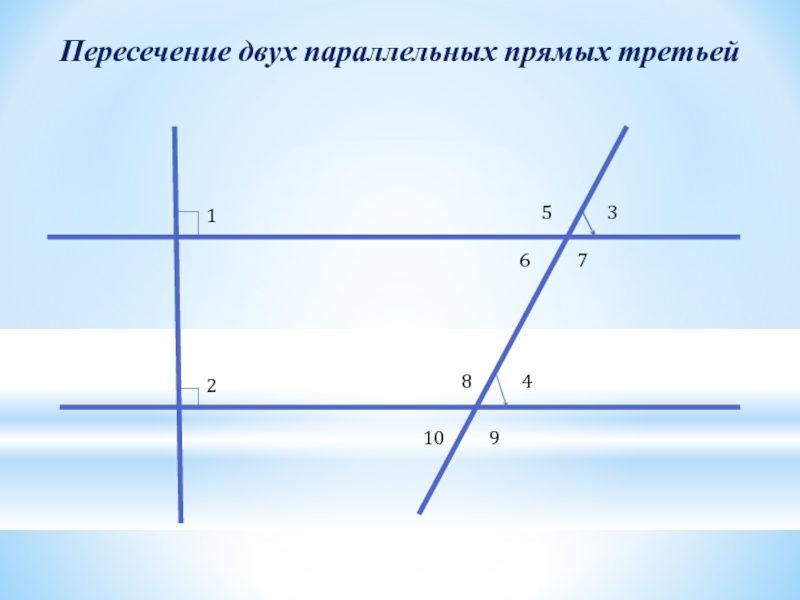
- 30. Пересечение двух параллельных прямых третьей12345678910
- 31. Вывод:При пересечении двух параллельных прямых третьей, образуются пары равных углов
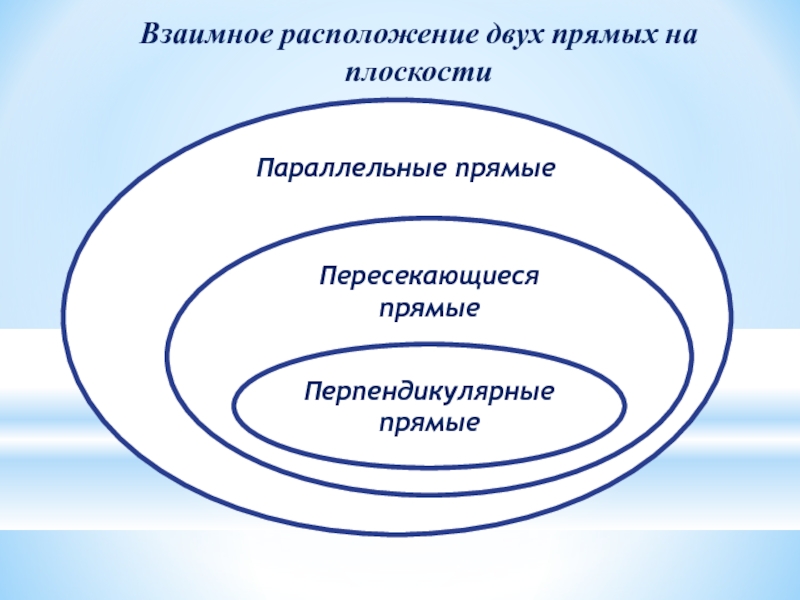
- 32. Перпендикулярные прямыеВзаимное расположение двух прямых на плоскостиПересекающиеся прямыеПараллельные прямые
- 33. Спасибо за урок!
- 34. Домашнее заданиеП.44 (знать правила, №1384, №1385, №1387, №1389(а).
123456Углы от 0 до 180 градусов
Слайд 13«Параллельные прямые»
Евкли́д или Эвкли́д
(3 в. до н. э.) древнегреческий математик, автор первого из дошедших
до нас теоретических трактатов по математике «Начала»
Слайд 14Никола́й Ива́нович Лобаче́вский — русский математик, создатель неевклидовой геометрии Лобачевский считает аксиому параллельности Евклида произвольным ограничением.
В качестве альтернативы предлагает другую аксиому: на плоскости через точку, не лежащую на данной прямой, проходит более чем одна прямая, не пересекающая данную.»
Слайд 20 Парфенон
Храм Афины Парфенос в Афинах 447-438 гг.
до н. э.
Храм имеет по 8 колонн Храм имеет по 8 колонн на фасадах Храм имеет по 8 колонн на фасадах , по 17 по бокам и портики с 39 колоннами.
Шедевры мировой архитектуры
Слайд 21Исаакиевский собор
Построен в 1818Построен в 1818—1858 годы по проекту архитектора Огюста Монферрана; строительство курировал император Николай I.
Имеет четыре 12-тиколонных портика и 24 верхних колонны.
Слайд 22Казанский собор
Построен на Невском проспекте в 1801—1811 годах архитектором А. Н. Воронихиным в 1801—1811 годах архитектором
А. Н. Воронихиным для хранения чтимого списка чудотворной иконы Божией Матери Казанской. Имеет колоннаду из 96-и колонн и внутри храма расположены 56 колонн.
Слайд 32
Перпендикулярные прямые
Взаимное расположение двух прямых на плоскости
Пересекающиеся прямые
Параллельные прямые
