- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад Введение в комбинаторику
Содержание
- 1. Презентация Введение в комбинаторику
- 2. Лавлинский М.В., LavlinskiMV@mail.ruДжеймс Джозеф Сильвестр(1814 — 1897)«Число,
- 3. - Наука изучающая, комбинации, которые можно составить
- 4. II. Перебор вариантов Задача №1.Сколько четных двузначных
- 5. Задача №2. Проводится игра. Из коробочки, содержащей
- 6. III. Правило умноженияЕсли элемент А может быть
- 7. Задача №5. Сколько существует способов занять 1-ое,
- 8. Задача №6. Несколько стран в качестве символа
- 9. Задача №6. Несколько стран в качестве символа
- 10. Задача №7.Сколькими способами можно посадить шестерых школьников
- 11. Задача №8.Азбука Морзе позволяет кодировать символы для
- 12. Задача №9.Какое наименьшее число символов должно быть
- 13. Задача №10.Каждая ячейка памяти компьютера, работающего в
- 14. M - мощность алфавита –количество символов в
- 15. Домашнее задание*Конспект«10_[ДЗ]Введение в комбинаторику.doc»СР «Введение в комбинаторику»
Слайд 2Лавлинский М.В., LavlinskiMV@mail.ru
Джеймс Джозеф Сильвестр
(1814 — 1897)
«Число, место и комбинация –
Слайд 3- Наука изучающая, комбинации, которые можно составить из заданных объектов
(От лат.
I. Комбинаторика
Г.В. Лейбниц –
ввёл термин «комбинаторика»
«Об искусстве комбинаторики» (1666 г.)
Комбинаторные задачи (КЗ) –
задачи, направленные на подсчет числа комбинаций
Методы решения КЗ:
Перебор вариантов
Правило умножения
Применение комбинаторных формул
Слайд 4II. Перебор вариантов
Задача №1.
Сколько четных двузначных чисел можно составить из
0, 1, 2, 4, 5, 9?
Решение:
10
12
14
20
22
24
40
42
44
50
52
54
90
92
94
Ответ: 15
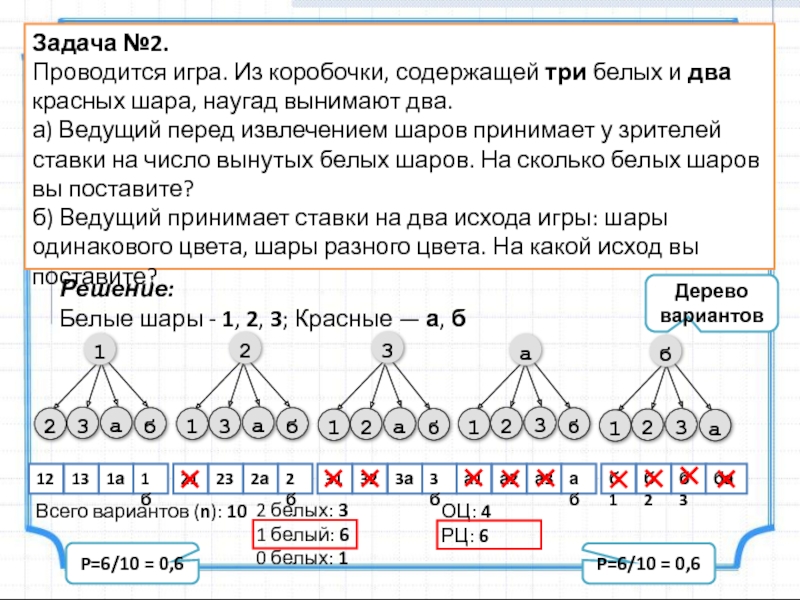
Слайд 5Задача №2.
Проводится игра. Из коробочки, содержащей три белых и два
а) Ведущий перед извлечением шаров принимает у зрителей ставки на число вынутых белых шаров. На сколько белых шаров вы поставите?
б) Ведущий принимает ставки на два исхода игры: шары одинакового цвета, шары разного цвета. На какой исход вы поставите?
Решение:
Белые шары - 1, 2, 3; Красные — а, б
2
3
а
б
1
1
3
а
б
1
2
а
б
1
2
3
б
1
2
3
а
3
а
б
2
12
13
1а
1б
21
23
2а
2б
31
32
3а
3б
а1
а2
а3
аб
б1
б2
б3
ба
Всего вариантов (n): 10
2 белых: 3
1 белый: 6
0 белых: 1
ОЦ: 4
РЦ: 6
P=6/10 = 0,6
P=6/10 = 0,6
Дерево вариантов
Слайд 6III. Правило умножения
Если элемент А может быть выбран k1 способами, а
Задача №3.
Сколько различных двузначных чисел можно составить из цифр:
1, 3, 5, 7, 9?
Решение:
Дано:
k1 = 5
k2 = 5
Найти:
N - ?
N = k1⋅k2
N = 5 ⋅ 5 = 25
Ответ: 25
Задача №4.
Сколько различных двузначных чисел кратных 5 можно составить из цифр:
1, 3, 5, 7, 9?
Решение:
Дано:
k1 = 5
k2 = 1
Найти:
N - ?
N = k1⋅k2
N = 5 ⋅ 1 = 5
Ответ: 5
Слайд 7Задача №5.
Сколько существует способов занять 1-ое, 2-ое и 3-е места
а) 10 команд
Решение:
N = 10 ⋅ 9 ⋅ 8 = 720
б) 11 команд?
Решение:
N = 11 ⋅ 10 ⋅ 9 = 990
Слайд 8Задача №6.
Несколько стран в качестве символа своего государства решили использовать
а)Сколько всего стран могут использовать такую символику?
Решение:
N=4 ⋅ 3 ⋅ 2 ⋅ 1 = 24
б) Сколько стран могут использовать такую символику с синей и красной полосами, расположенными рядом?
Решение:
N = 2 ⋅ (3 ⋅ 2 ⋅ 1) = 12
(т.к. возможно синяя-красная, или красная-синяя)
Слайд 9Задача №6.
Несколько стран в качестве символа своего государства решили использовать
в) Сколько всего стран могут использовать такую символику с нижней белой полосой?
Решение:
N = 3 ⋅ 2 ⋅ 1 = 6
г) Сколько стран могут использовать такую символику с верхней белой полосой?
Решение:
N = 3 ⋅ 2 ⋅ 1 = 6
Слайд 10Задача №7.
Сколькими способами можно посадить шестерых школьников на скамейку так, чтобы
Решение:
Способ 1. См. задачу 6
Способ 2.
k1 = 6 (Способы посадить Мишу)
k2 = 1 или 2 (Способы посадить Олю рядом)
Это зависит от того, куда мы посадили Мишу
1) Миша сидит на краю
N1 = 2 ⋅ 1 ⋅ 4 ⋅ 3 ⋅ 2 ⋅ 1 = 48 способов
2) Миша сидит не на краю
N2 = 4 ⋅ 1 ⋅ 4 ⋅ 3 ⋅ 2 ⋅ 1 = 192 способа
3) N = 48 + 192 = 240
Ответ: 240
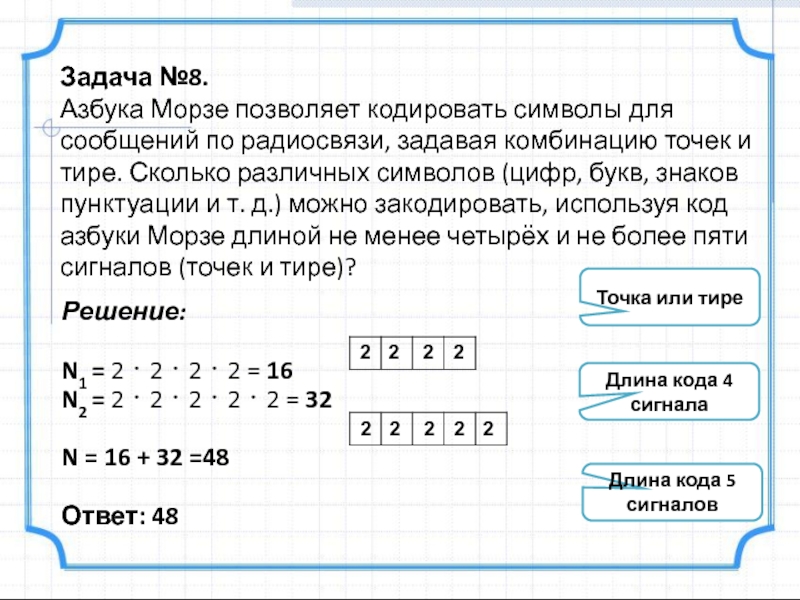
Слайд 11Задача №8.
Азбука Морзе позволяет кодировать символы для сообщений по радиосвязи, задавая
Решение:
N1 = 2 ⋅ 2 ⋅ 2 ⋅ 2 = 16
N2 = 2 ⋅ 2 ⋅ 2 ⋅ 2 ⋅ 2 = 32
N = 16 + 32 =48
Ответ: 48
Длина кода 4 сигнала
Длина кода 5 сигналов
2
Точка или тире
2
2
2
2
2
2
2
2
Слайд 12Задача №9.
Какое наименьшее число символов должно быть в алфавите, чтобы при
3-ех буквенные слова
х
х
х
Решение:
N = х ⋅ х ⋅ х ≥ 9
⇒
х = 3
Ответ: 3
Слайд 13Задача №10.
Каждая ячейка памяти компьютера, работающего в троичной системе счисления, может
Решение:
N = 3 ⋅ 3 ⋅ 3 ⋅ 3 = 81
Ответ: 81
3
3
3
3
Слайд 14
M - мощность алфавита –количество символов в этом алфавите
Q - количество
N – длина «слов» (без учета смысла)
IV. Формула










![Презентация Введение в комбинаторику Домашнее задание*Конспект«10_[ДЗ]Введение в комбинаторику.doc»СР «Введение в комбинаторику» Домашнее задание*Конспект«10_[ДЗ]Введение в комбинаторику.doc»СР «Введение в комбинаторику»](/img/thumbs/f09fff7a69947c0a3df3022e8851def4-800x.jpg)





