Чубарых» Красненского района
Белгородской области
- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад Векторы на плоскости
Содержание
- 1. Презентация Векторы на плоскости
- 2. Примеры из физики
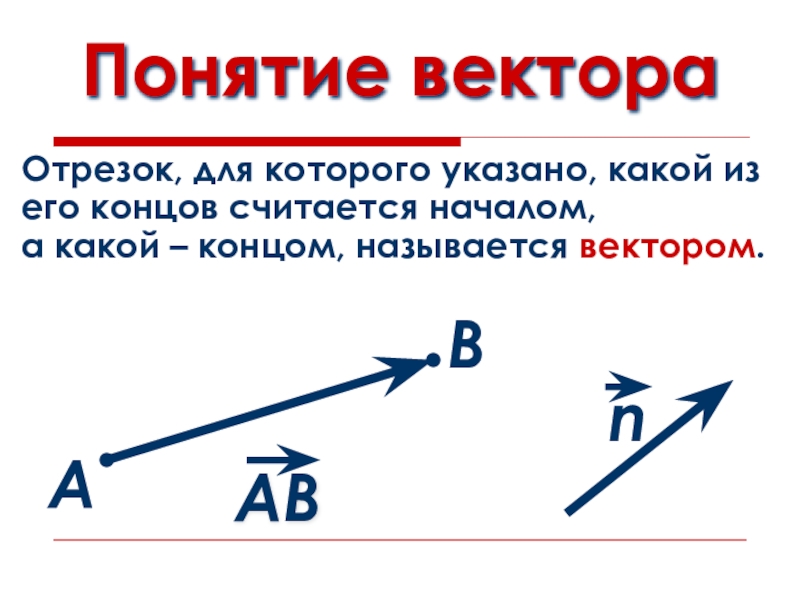
- 3. Понятие вектораАВОтрезок, для которого указано, какой из его концов считается началом,а какой – концом, называется вектором.
- 4. Нулевой векторЛюбая точка на плоскости может рассматриваться как вектор. МТакой вектор называется нулевым.
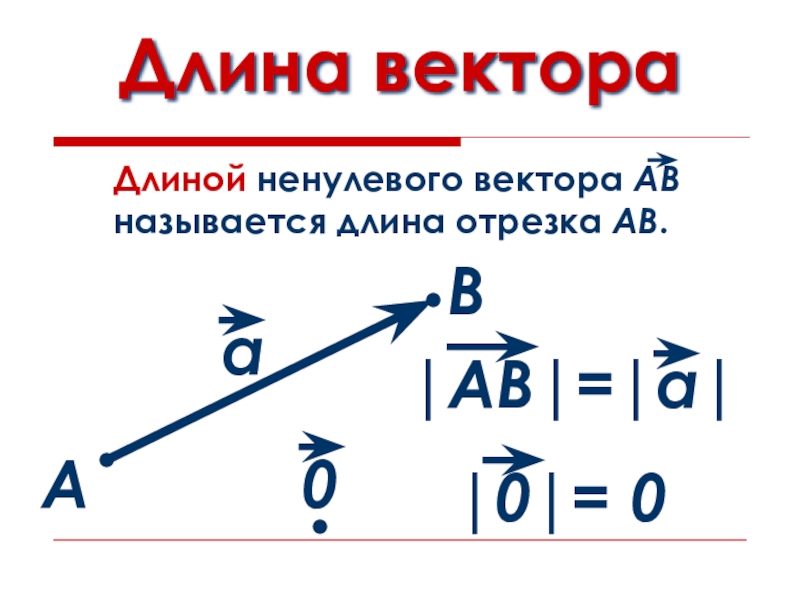
- 5. Длина вектораАВ
- 6. Коллинеарность векторовДва ненулевых вектора называются коллинеарными, если
- 7. Сонаправленные векторыДва коллинеарных вектора называются сонаправленными, если у них совпадают направления.
- 8. Противоположно направленные векторыДва коллинеарных вектора называются противоположно направленными, если они не сонаправлены.
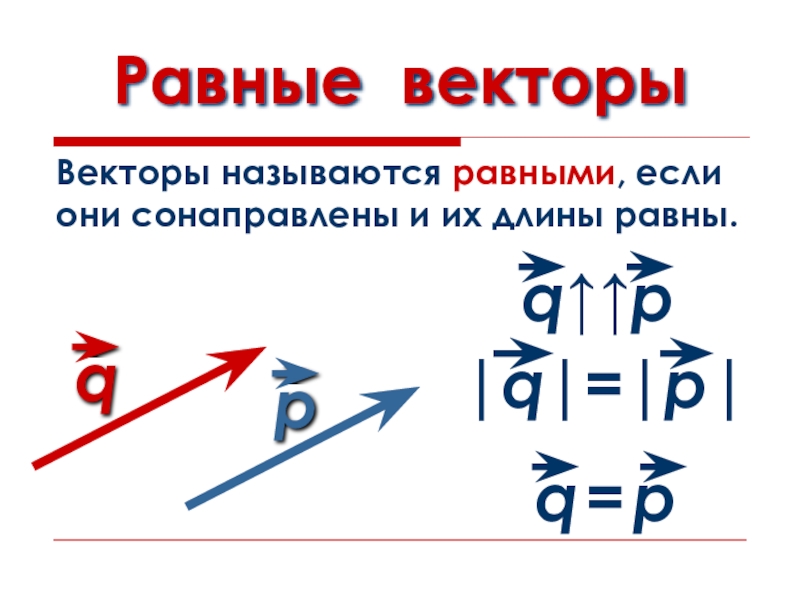
- 9. Равные векторыВекторы называются равными, если они сонаправлены и их длины равны.
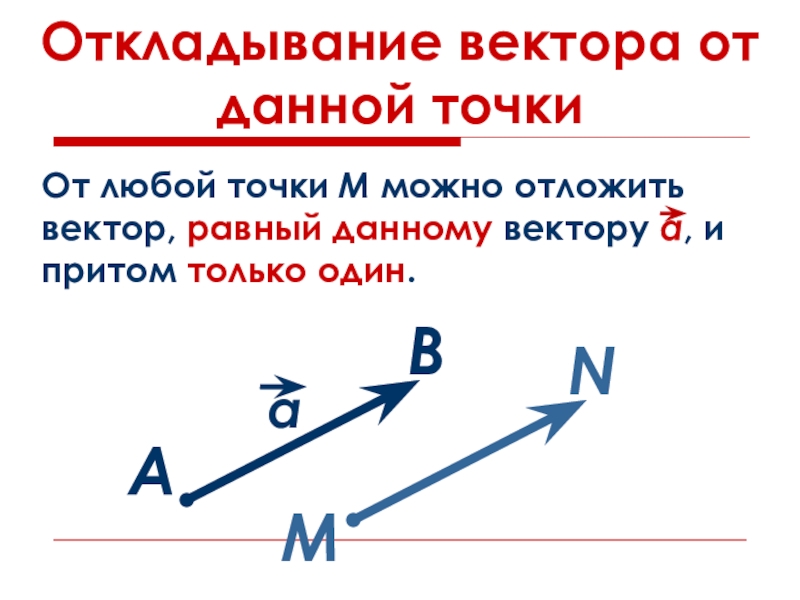
- 10. Откладывание вектора от данной точкиАВМN
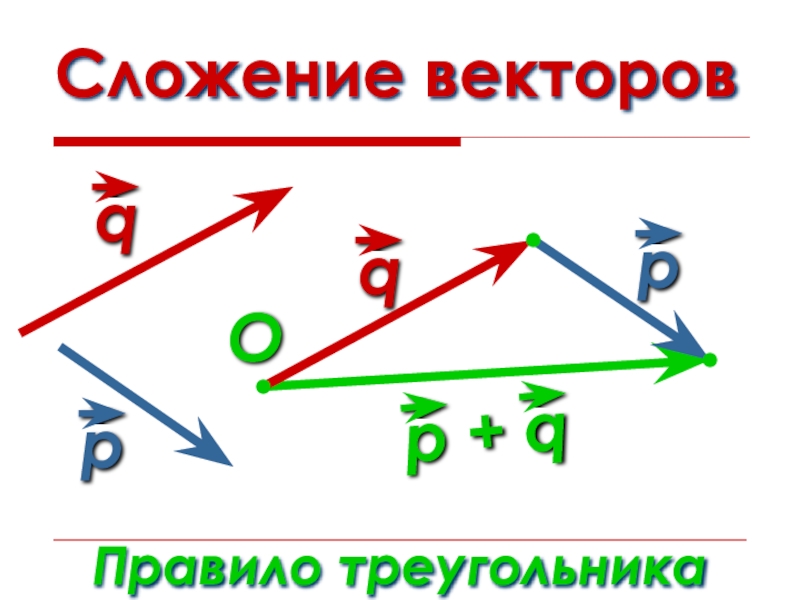
- 11. Сложение векторовПравило треугольникаO
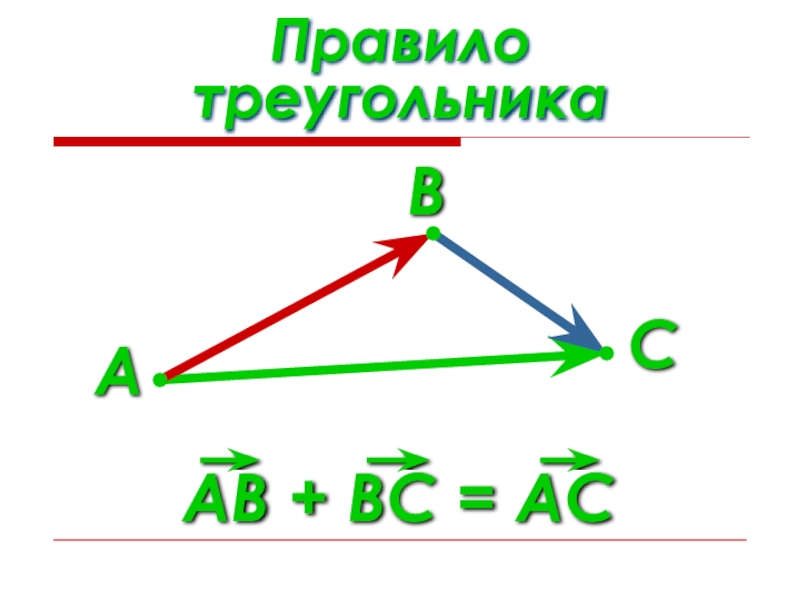
- 12. Правило треугольникаАВС
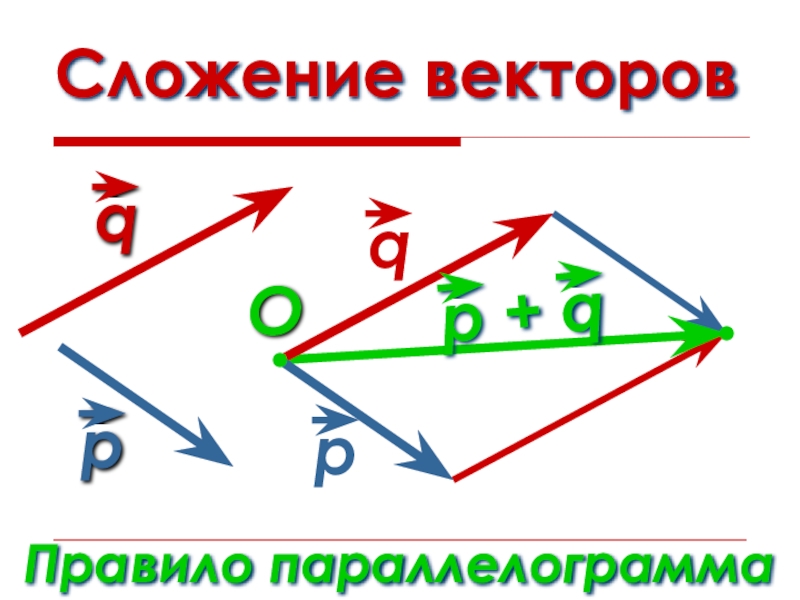
- 13. Сложение векторовПравило параллелограммаO
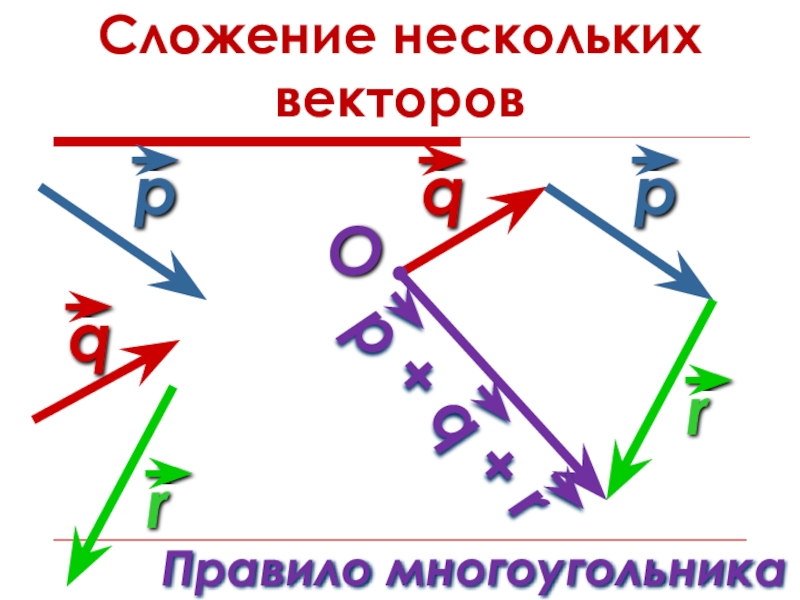
- 14. Сложение нескольких векторовOПравило многоугольника
- 15. Свойства сложения− переместительный закон− сочетательный закон− разность векторов
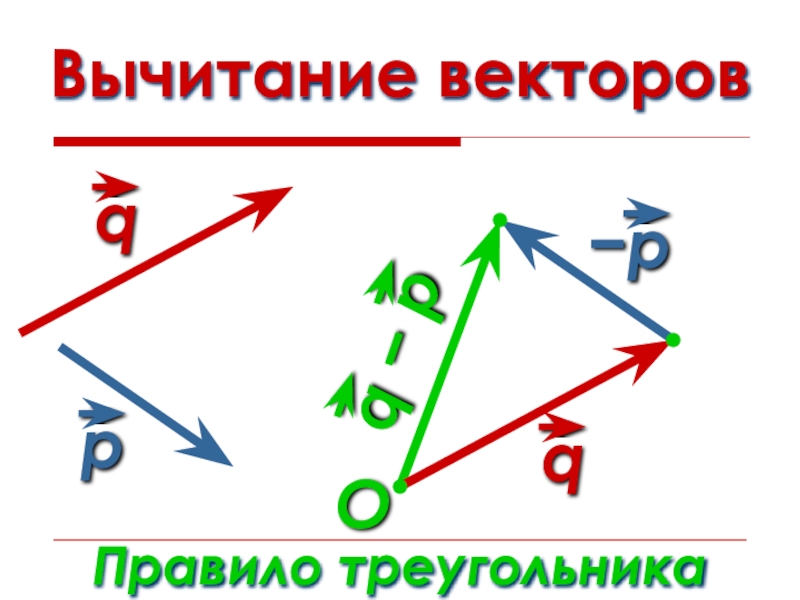
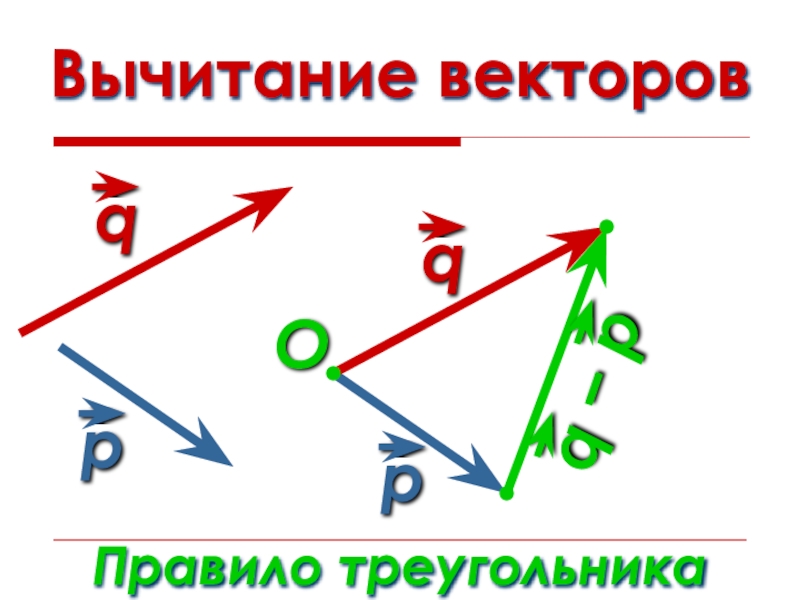
- 16. Вычитание векторовПравило треугольникаO
- 17. Вычитание векторовПравило треугольникаO
- 18. Умножение вектора на число
- 19. Свойства умножения− первый распределительный закон− сочетательный закон− второй распределительный закон
- 20. Применение векторов к решению задач
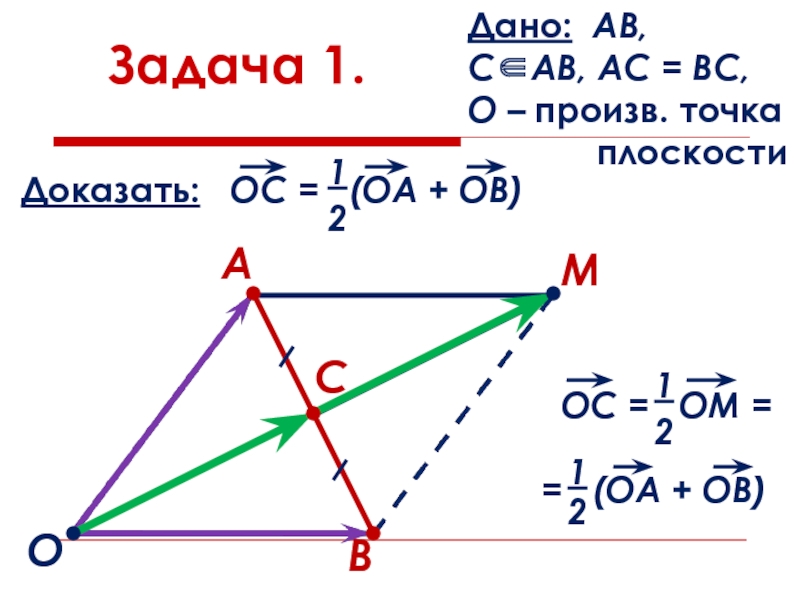
- 21. Задача 1.Дано: АВ, С∈АВ, АС = ВС,
- 22. Задача 2.Дано: АВСD – трапеция, М∈ВС, N∈AD,
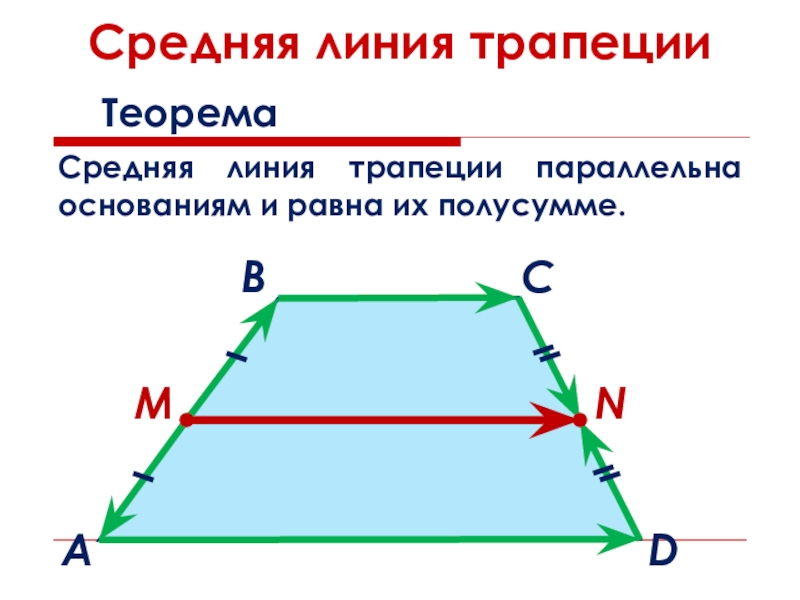
- 23. Средняя линия трапецииТеорема Средняя линия трапеции параллельна основаниям и равна их полусумме. MNBACD
Примеры из физики
Слайд 1Векторы на плоскости
Учитель математики: Хантулина Татьяна Павловна
МОУ «Большовская оош имени М.Д.
Слайд 3Понятие вектора
А
В
Отрезок, для которого указано, какой из
его концов считается началом,
а
какой – концом, называется вектором.
Слайд 4Нулевой вектор
Любая точка на плоскости может
рассматриваться как вектор.
М
Такой вектор
называется нулевым.
Слайд 6Коллинеарность векторов
Два ненулевых вектора называются
коллинеарными, если они лежат на одной
прямой или на параллельных прямых.
Слайд 7Сонаправленные векторы
Два коллинеарных вектора
называются сонаправленными,
если у них совпадают направления.
Слайд 8Противоположно направленные векторы
Два коллинеарных вектора называются
противоположно направленными, если
они не
сонаправлены.
Слайд 19Свойства умножения
− первый распределительный закон
− сочетательный закон
− второй распределительный закон
Слайд 22
Задача 2.
Дано:
АВСD – трапеция,
М∈ВС, N∈AD,
BM = MC, AN
= ND
Доказать:
MN ∩ AВ ∩ DC = O
О
N
В
M
D
C
A
Слайд 23
Средняя линия трапеции
Теорема
Средняя линия трапеции параллельна основаниям и равна их
полусумме.
M
N
B
A
C
D