- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад в помощь учителю на тему: Показательная функция
Содержание
- 1. Презентация в помощь учителю на тему: Показательная функция
- 2. ЦЕЛЬ УРОКА: рассмотреть задачи Внешнего Независимого
- 3. Задачи урока: повторить свойство монотонности и ограниченности
- 4. Показательная функция.По закону показательной функции размножалось бы
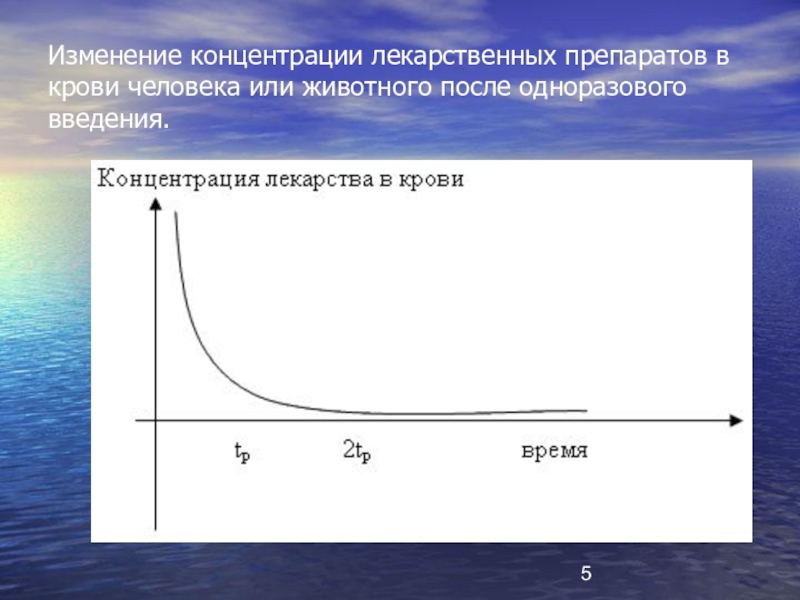
- 5. Изменение концентрации лекарственных препаратов в крови человека или животного после одноразового введения.
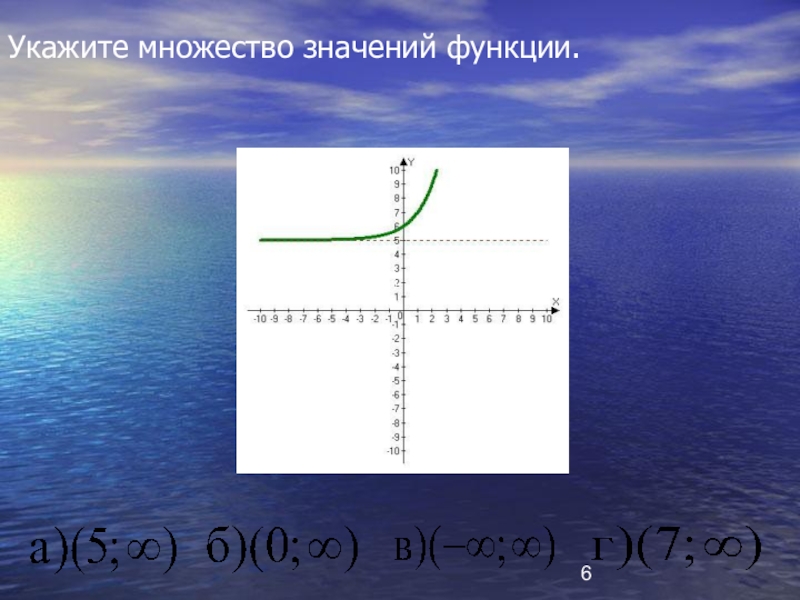
- 6. Укажите множество значений функции.а) (5;
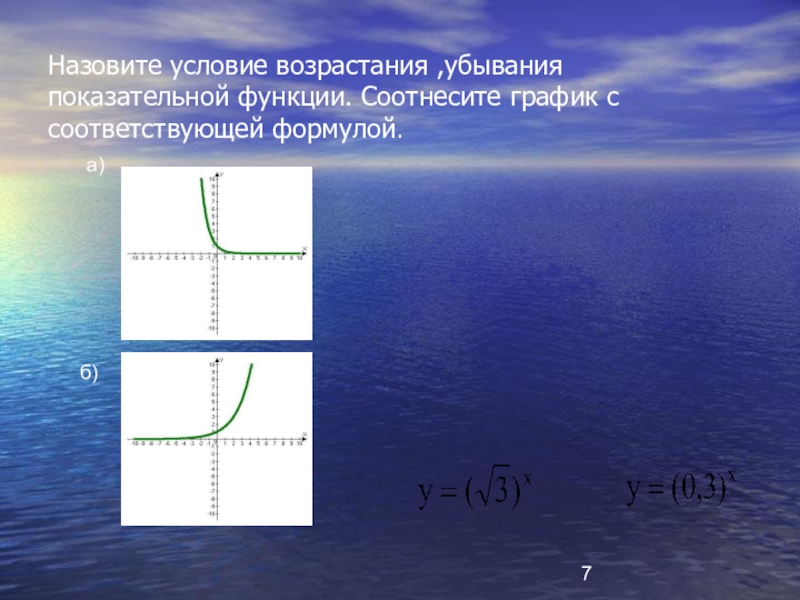
- 7. Назовите условие возрастания ,убывания показательной функции. Соотнесите график с соответствующей формулой.а)б)
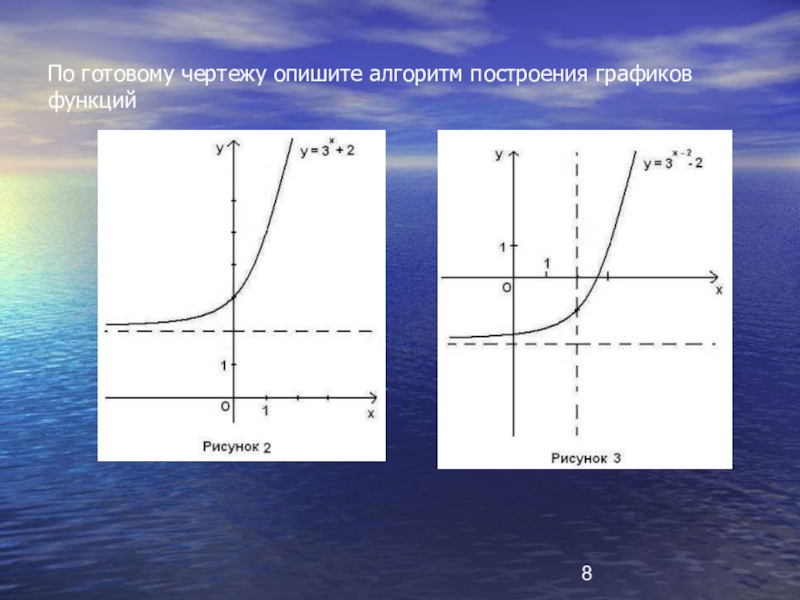
- 8. По готовому чертежу опишите алгоритм построения графиков функций
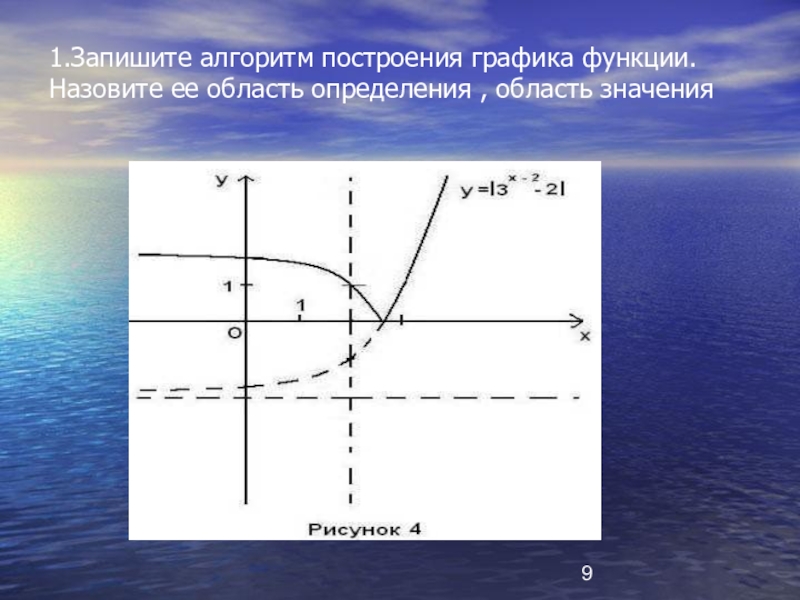
- 9. 1.Запишите алгоритм построения графика функции. Назовите ее область определения , область значения
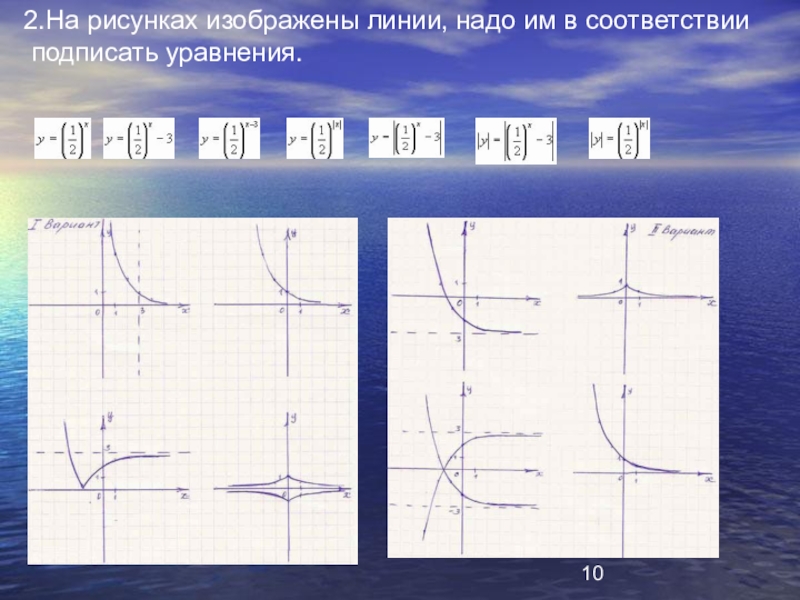
- 10. 2.На рисунках изображены линии, надо им в соответствии подписать уравнения.
- 11. 1. Какая из показательных функций является возрастающей?
- 12. 2.Найти область определения функции:
- 13. 3. Найти область значений функции:
- 14. 4. График функциииз графика функцииполучается А) параллельным
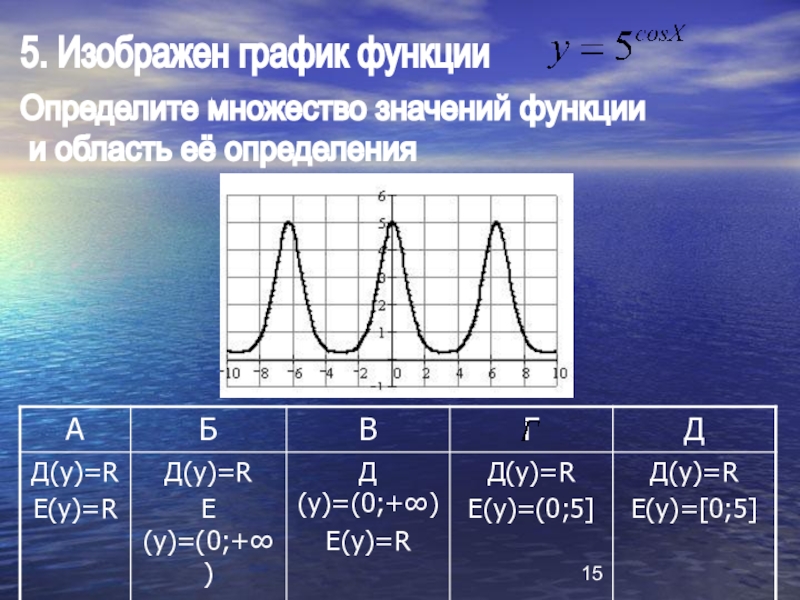
- 15. 5. Изображен график функцииОпределите множество значений функции и область её определения
- 16. 6. Определите при каком значении a функцияпроходит через точку Р(2;9)
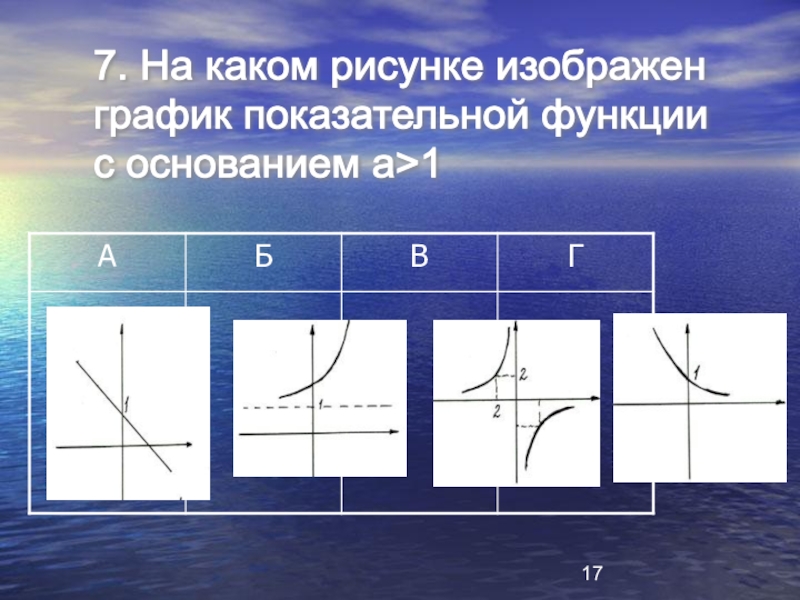
- 17. 7. На каком рисунке изображен график показательной функции с основанием а>1
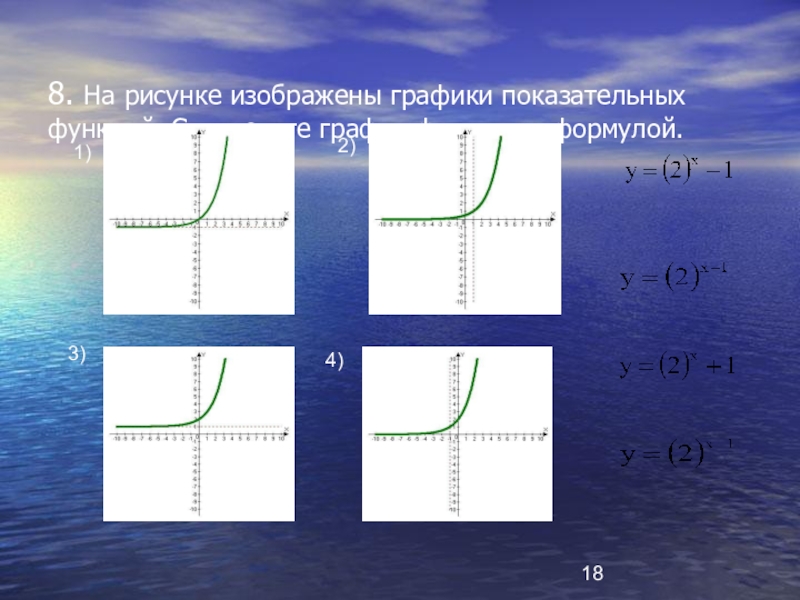
- 18. 8. На рисунке изображены графики показательных функций. Соотнесите график функции с формулой.1)2)3)4)
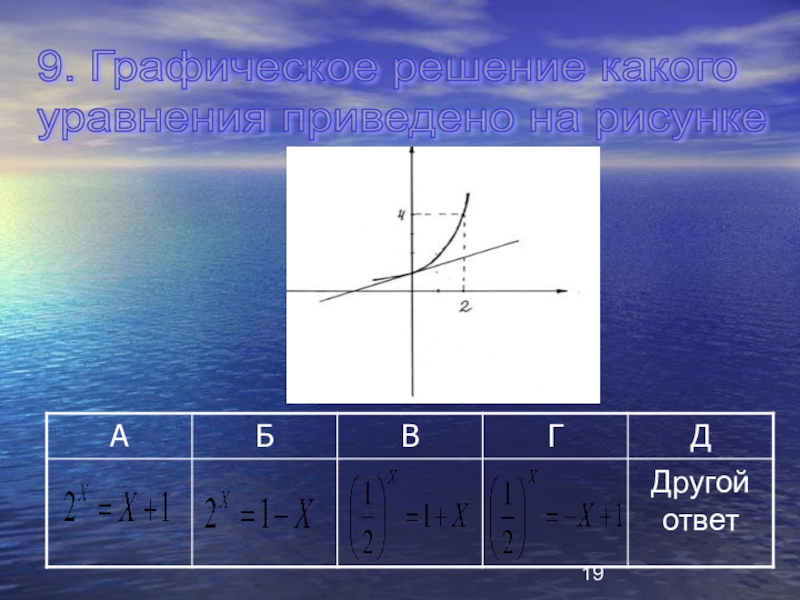
- 19. 9. Графическое решение какого уравнения приведено на рисунке
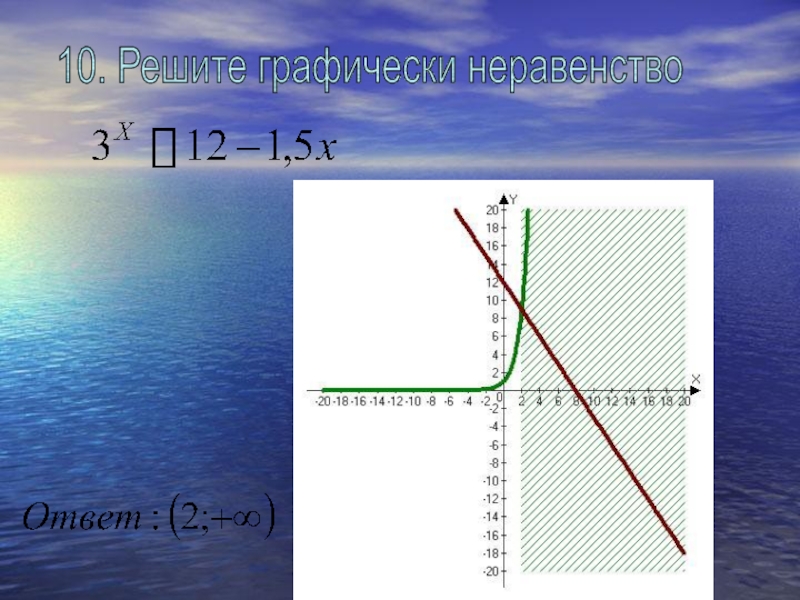
- 20. 10. Решите графически неравенство
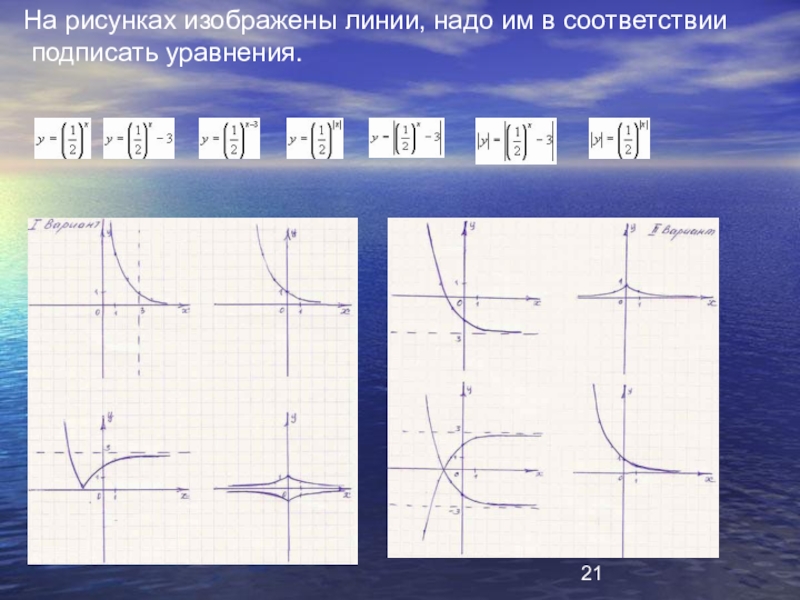
- 21. На рисунках изображены линии, надо им в соответствии подписать уравнения.
- 22. КАК РЕШИТЬ УРАВНЕНИЕ ВИДА: f(x)= g(x)?
- 23. Функционально-графический методЧтобы решить уравнение вида f(x)= g(x)
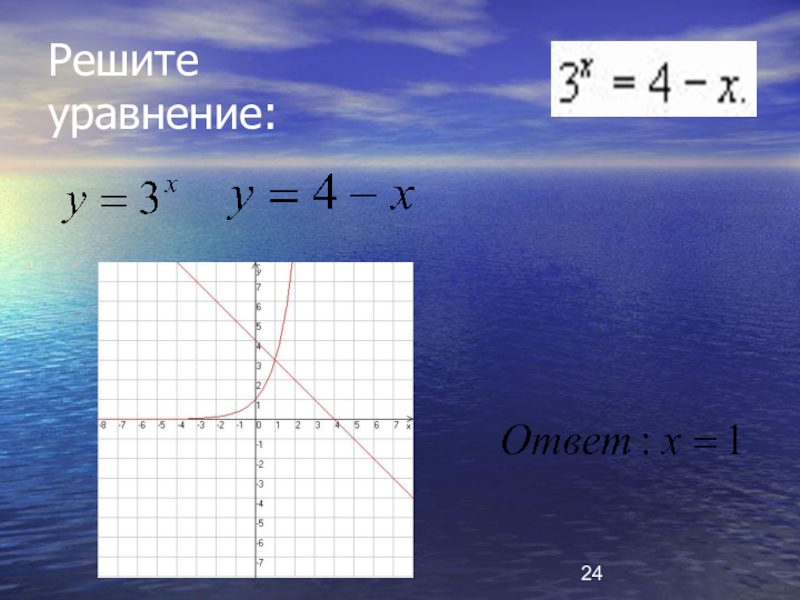
- 24. Решите уравнение:
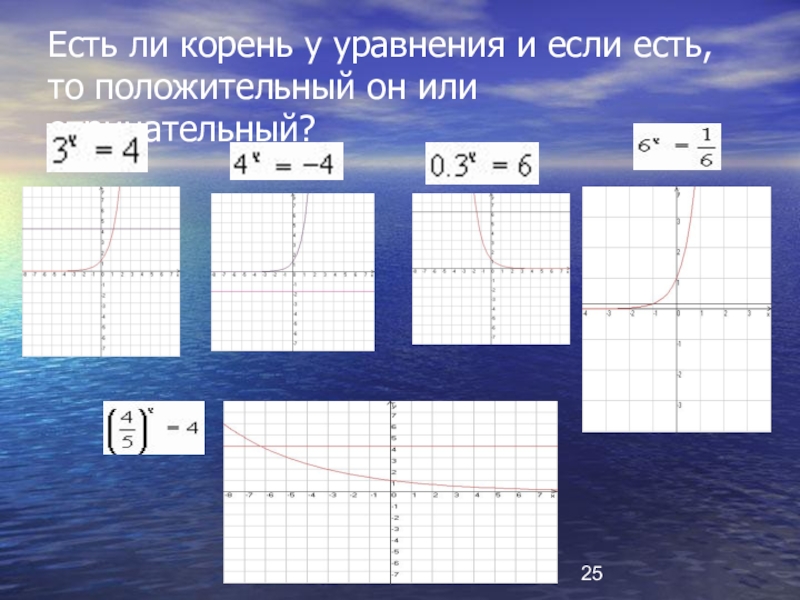
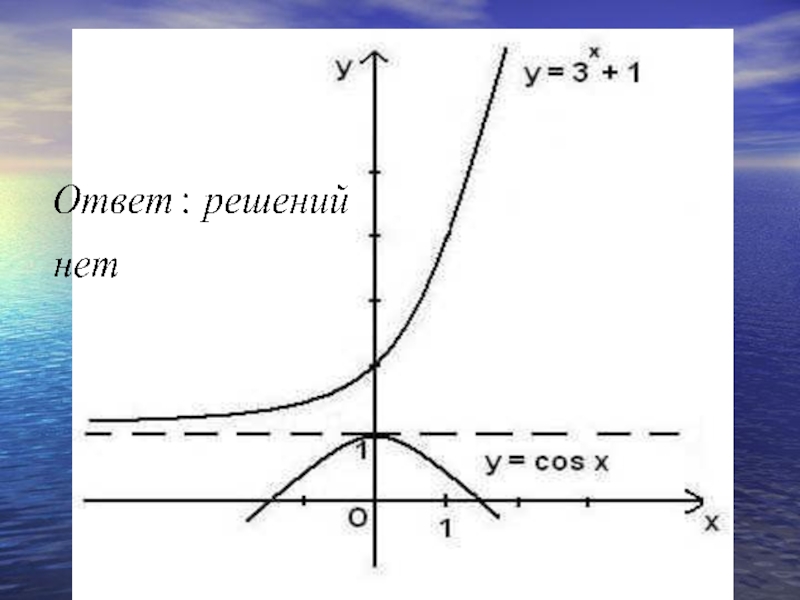
- 25. Есть ли корень у уравнения и если
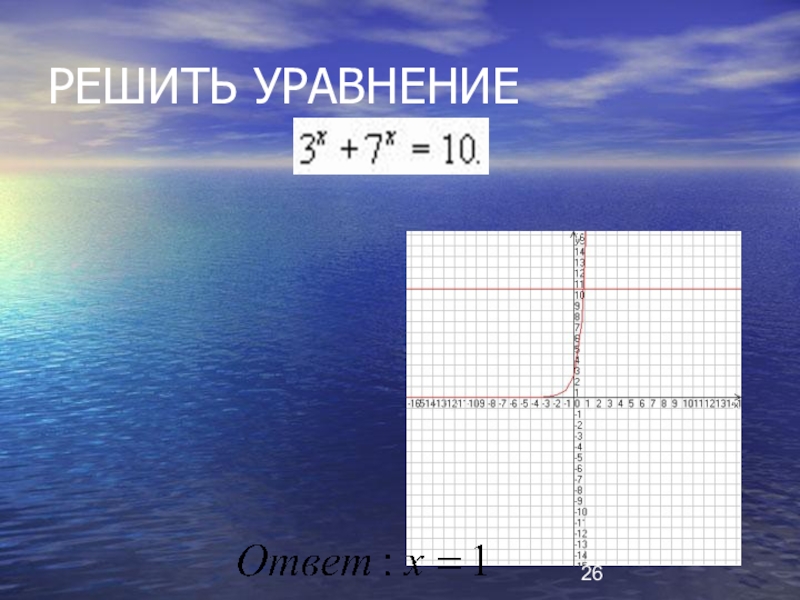
- 26. РЕШИТЬ УРАВНЕНИЕ
- 27. Практическая работа
- 28. .Решите уравнения:2.Решить неравенство4.Найдите область значений функции3.Найти значение
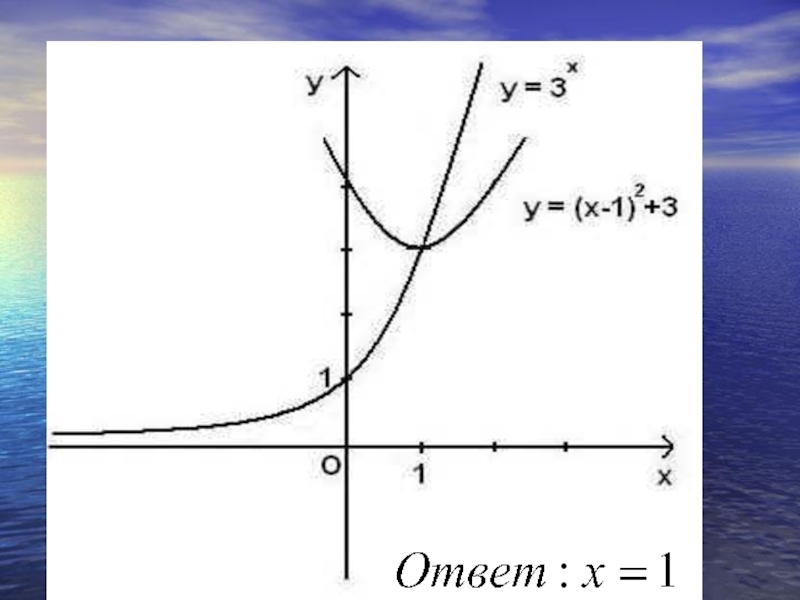
- 29. РЕШИТЬ УРАВНЕНИЕ
- 30. Слайд 30
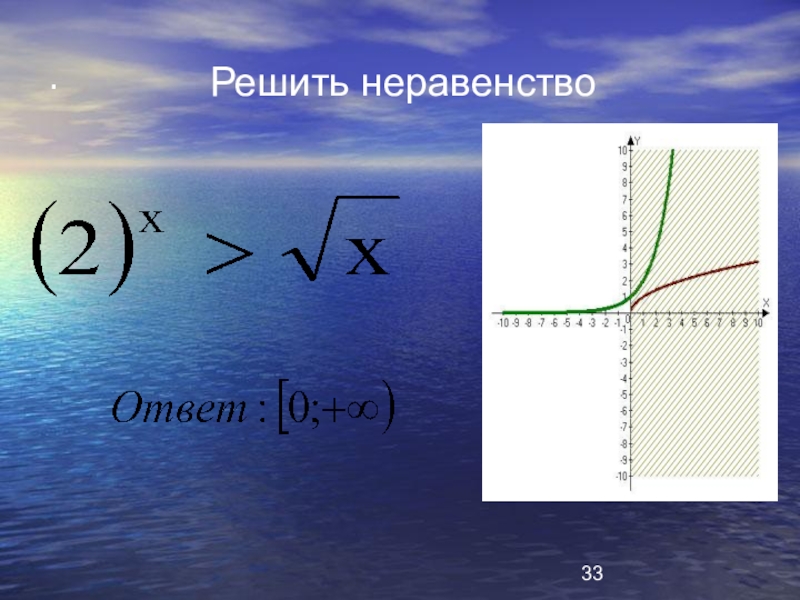
- 31. Решить неравенство
- 32. Слайд 32
- 33. .Решить неравенство
- 34. Укажите множество значений функции
- 35. РЕШИТЬ УРАВНЕНИЕРешая эту систему, находим, что х = 0.
- 36. Найти область значений функции
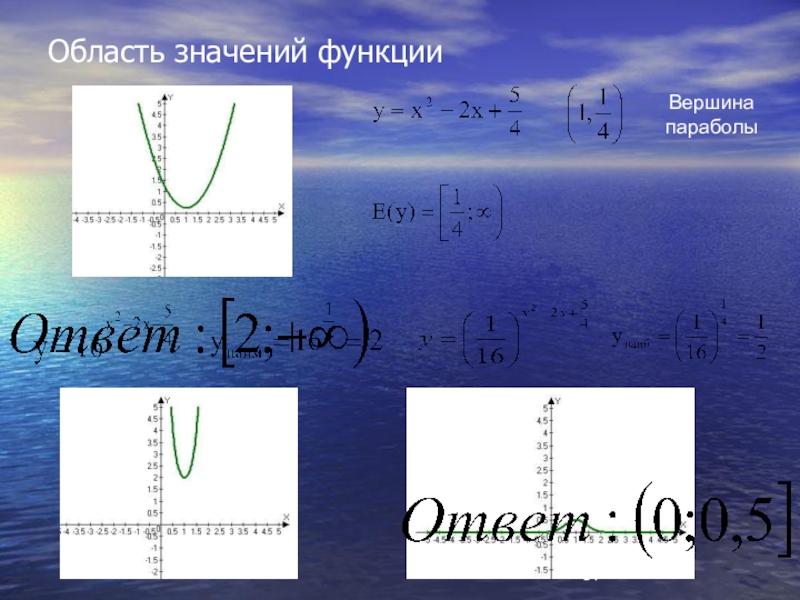
- 37. Область значений функцииВершина параболы
- 38. Решаем систему уравнений
- 39. Найти значение выражения
- 40. Решаем систему уравнений:
- 41. При каких значениях параметра а уравнение имеет нечетное количество корней?
- 42. Так как график четной функции симметричен относительно
- 43. Решить неравенствоОтвет: (-;2].Ответ: (-1;0)
- 44. Домашнее задание: Решить графически систему уравнений.Решите уравнениеРешите неравенство
- 45. ВСЕМ ОГРОМНОЕ СПАСИБО ЗА СОТРУДНИЧЕСТВО! ВАМ, ДЕТИ, ВЕСЕЛЫХ КАНИКУЛ!!!
Слайд 1Показательная функция.
«Функционально - графические методы решения уравнений неравенств и систем»
Учитель
СОШ № 84
Слайд 2ЦЕЛЬ УРОКА:
рассмотреть задачи Внешнего Независимого оценивания (ЗНО)
ПОКАЗАТЕЛЬНОЙ ФУНКЦИИ
Слайд 3Задачи урока:
повторить свойство монотонности и ограниченности показательной функции;
повторить алгоритм построения
находить множество значений и множество определений функции по виду формулы и с помощью графика;
решать показательные уравнения, неравенства и системы с помощью графиков и свойств функции.
работа с графиками функций, содержащими модуль;
рассмотреть графики сложной функции и их область значений;
Слайд 4Показательная функция.
По закону показательной функции размножалось бы все живое на Земле,
В природе, технике и экономике встречаются многочисленные процессы, в ходе которых значение величины меняется в одно и то же число раз, т.е. по закону показательной функции. Эти процессы называются процессами органического роста или органического затухания.
Например, рост бактерий в идеальных условиях соответствует процессу органического роста; радиоактивный распад веществ – процессу органического затухания.
Слайд 5Изменение концентрации лекарственных препаратов в крови человека или животного после одноразового
Слайд 7Назовите условие возрастания ,убывания показательной функции. Соотнесите график с соответствующей формулой.
а)
б)
Слайд 91.Запишите алгоритм построения графика функции. Назовите ее область определения , область
Слайд 144. График функции
из графика функции
получается
А) параллельным переносом вдоль оси Х
Б) параллельным переносом вдоль оси Х
на 2 единицы влево;
В) параллельным переносом вдоль оси Y
на 2 единицы вверх;
Г) параллельным переносом вдоль оси Y
на 2 единицы вниз;
Д) другой ответ.
Слайд 188. На рисунке изображены графики показательных функций. Соотнесите график функции с
1)
2)
3)
4)
Слайд 23Функционально-графический метод
Чтобы решить уравнение вида
f(x)= g(x) функционально-графическим методом нужно:
Построить графики
Определить абсциссы точек пересечения графиков данных функций.
Записать ответ.
Слайд 28.
Решите уравнения:
2.Решить неравенство
4.Найдите область значений функции
3.Найти значение выражения
Слайд 42Так как график четной функции симметричен относительно оси ординат
то если
является корнем уравнения, то и
тоже является корнем уравнения. Поэтому данное уравнение может
иметь нечетное количество корней только тогда, когда
является корнем. Подставляя
в уравнение, имеем:









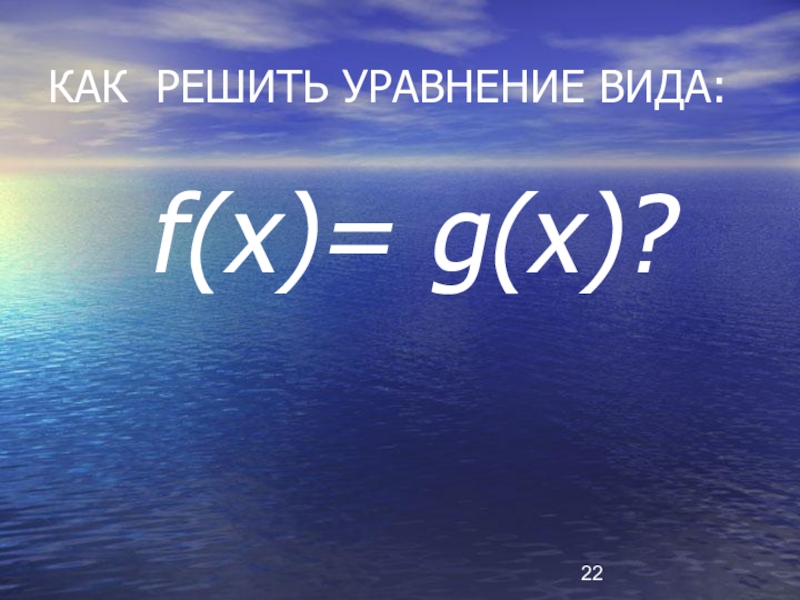



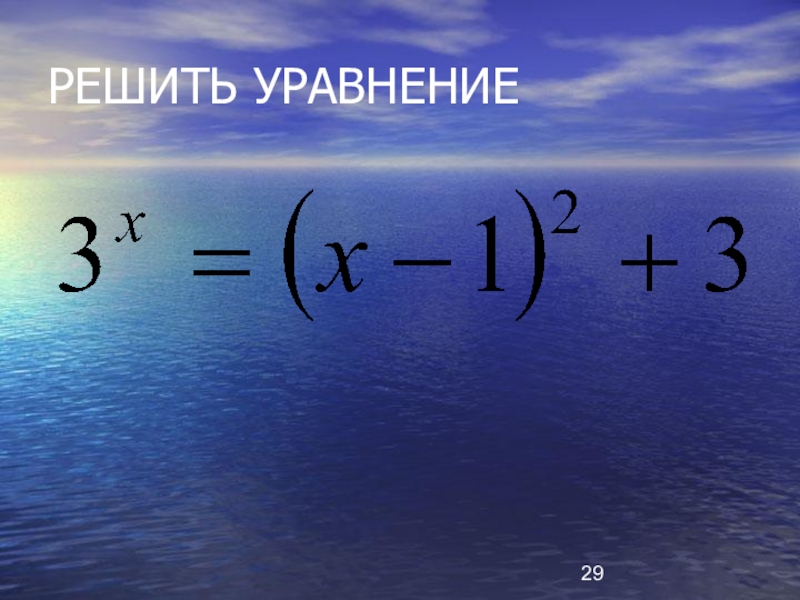









![Презентация в помощь учителю на тему: Показательная функция Решить неравенствоОтвет: (-;2].Ответ: (-1;0) Решить неравенствоОтвет: (-;2].Ответ: (-1;0)](/img/thumbs/c82c0f1aba09f5bbd235c99ce43ae745-800x.jpg)







