- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад урока по теме Формулы приведения
Содержание
- 1. Презентация урока по теме Формулы приведения
- 2. План урока:Проверка домашнего заданияАктуализация знанийВыполнение упражненийСтраничка ЕГЭИсторическая справка (презентация)Задание на дом.Итог урока.
- 3. «Нет ни одной области математики, которая когда-нибудь
- 4. Домашняя работаВыполнила Рябцева Наталья
- 5. №667(2)
- 6. №668(2)
- 7. №675(2,4,6)2)
- 8. 6)
- 9. Устная работаВ какой четверти находится точка, полученная
- 10. 3. Может ли быть верным равенство?
- 11. Упростить: 2 sinα cos α
- 12. Упросить:Sin (π/2- α)
- 13. Выполнение упражнений. № 671 (1,2)2)Sin 25π/
- 14. №673(3;1)sin(7π /6 + α) = - sin
- 15. № 672(1,3)Sin (π/4 + α) - cos
- 16. Страничка ЕГЭ.Найти значение выражения: cos119°· sin 31° + cos29°· cos31°____________________________ sin 17°·sin103° + cos17°· sin13°
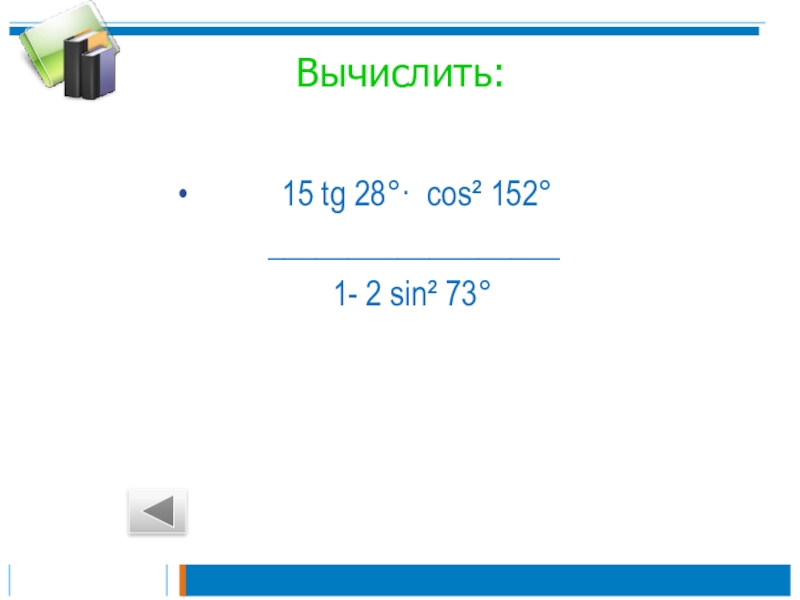
- 17. Вычислить: 15 tg
- 18. Историческая справкаТригонометрияВыполнил: Кузьмин И.
- 19. Как и
- 20. Долгие годы
- 21. Первый
- 22. Следует
- 23. Домашнее задание. § 34 №
- 24. Итог урока. Мы познакомились с формуламиприведения, учились
- 25. Математический диктант. Продолжи предложение:Чтобы записать любую из
- 26. Продолжи равенство:2. sin(π/2+α)=
- 27. Проверим
- 28. 2. sin(π/2+α)= cosα
- 29. Рефлексия.Результатом своей личной работы считаю, что я
- 30. Рефлексия.Результатом своей личной работы считаю, что я
План урока:Проверка домашнего заданияАктуализация знанийВыполнение упражненийСтраничка ЕГЭИсторическая справка (презентация)Задание на дом.Итог урока.
Слайд 2План урока:
Проверка домашнего задания
Актуализация знаний
Выполнение упражнений
Страничка ЕГЭ
Историческая справка (презентация)
Задание на дом.
Итог
урока.
Слайд 3«Нет ни одной области математики, которая когда-нибудь не окажется применимой к
явлениям действительного мира».
Н.И. Лобачевский.
Н.И. Лобачевский.
Слайд 9Устная работа
В какой четверти находится точка, полученная поворотом точки Р (1;0)
вокруг начало координат на угол
836° ; -134 ° ; 286° ; 405° ; - 208°
2. В какой четверти лежит угол α , если выполняется условие
a) sin α > 0, cos α < 0
b) sin α < 0, tg α >0
836° ; -134 ° ; 286° ; 405° ; - 208°
2. В какой четверти лежит угол α , если выполняется условие
a) sin α > 0, cos α < 0
b) sin α < 0, tg α >0
Слайд 103. Может ли быть верным равенство?
sin² x +
cos² x = -⅓
sin² 2x + cos² 2x = 1
sin² x/2 + cos² x/2 = 3/2
4. Что больше? Сos π или sin π/2
cos 0 или sin π ; sin 3π/2 или cos π
sin² 2x + cos² 2x = 1
sin² x/2 + cos² x/2 = 3/2
4. Что больше? Сos π или sin π/2
cos 0 или sin π ; sin 3π/2 или cos π
Слайд 11Упростить: 2 sinα cos α
__________ ;
cos²α - sin²α
1- cos²α
_________ - tg ²α ; 7 cos²α - 5 + 7 sin²α ;
Cos²α
tg (- α) + cos²(-α) - sin²(-α) – tg (-α);
1- cos 2α 6 cos²2α
------------- ; -------------
Sin²α 1+ cos4α
cos²α - sin²α
1- cos²α
_________ - tg ²α ; 7 cos²α - 5 + 7 sin²α ;
Cos²α
tg (- α) + cos²(-α) - sin²(-α) – tg (-α);
1- cos 2α 6 cos²2α
------------- ; -------------
Sin²α 1+ cos4α
Слайд 12Упросить:
Sin (π/2- α)
cos (3π/2 + α )
Tg (π + α) ctg (π/2 + α )
Cos (π - α ) cos (3π/2 - α )
Sin (π+ α ) tg(π/2 - α )
Вычислить:
Sin 150° cos 405°
Tg 210° ctg 300°
Cos 120° cos 225°
Tg (π + α) ctg (π/2 + α )
Cos (π - α ) cos (3π/2 - α )
Sin (π+ α ) tg(π/2 - α )
Вычислить:
Sin 150° cos 405°
Tg 210° ctg 300°
Cos 120° cos 225°
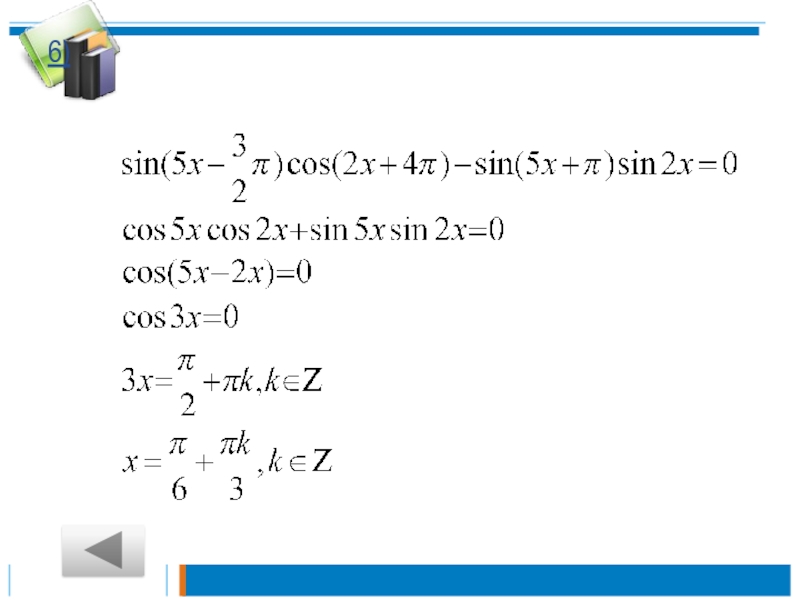
Слайд 13Выполнение упражнений.
№ 671 (1,2)
2)Sin 25π/ 3 – cos (-17π/ 2)–tg10π/3=
sin (8π + π /3)
– cos 8,5 π – tg(3π + π /3) = √3/2 – 0 - √3 =- √3/2
– cos 8,5 π – tg(3π + π /3) = √3/2 – 0 - √3 =- √3/2
Слайд 14№673(3;1)
sin(7π /6 + α) = - sin (π /6 +α )
sin(7π /6 + α) = sin (π+ (π /6 +α))=
- sin (π /6 +α )
лев.ч. = прав.ч
- sin (π /6 +α )
лев.ч. = прав.ч
Слайд 15№ 672(1,3)
Sin (π/4 + α) - cos (π/4 - α) =
0
Sin π/4 · cos α + Sin α · cos π/4 -
- cos π/4 · cos α - sinα · sin π/4 =
= √2/2 cos α + Sin α · √2/2 - √2/2 · cos α - sinα · √2/2 =0
3) ctgα· ctg(3π/2 + α) = -1
ctgα· (-tg α) = -1
-1=-1
Sin π/4 · cos α + Sin α · cos π/4 -
- cos π/4 · cos α - sinα · sin π/4 =
= √2/2 cos α + Sin α · √2/2 - √2/2 · cos α - sinα · √2/2 =0
3) ctgα· ctg(3π/2 + α) = -1
ctgα· (-tg α) = -1
-1=-1
Слайд 16 Страничка ЕГЭ.
Найти значение выражения:
cos119°· sin 31° + cos29°· cos31°
____________________________
sin 17°·sin103° + cos17°· sin13°
Слайд 19 Как и многие разделы математики, тригонометрия
возникла в древние времена из потребностей людей при ведение расчетов, связанных с земельными работами (для определения расстояния до недоступных предметов, составления географических карт и пр.). Еще древнегреческие ученые создали «тригонометрию хорд», в которой выражались зависимости между центральными углами кругу и хордами, на которых они опираются. Этой тригонометрией пользовался во II в. До н. э. в своих расчетах древнегреческий астроном Гиппарх. Во II в. н.э. греческий ученый Птолемей в своей работе «Алмагест» («Великая книга») вывел соотношения в круге, которые по сути своей аналогичны современным формулам синуса половинного и двойного углов, синуса суммы и разности двух углов.
Слайд 20 Долгие годы тригонометрия служила и развивалась
благодаря астрономии. В VIII в. Усилиями математиков Ближнего и Среднего Востока тригонометрия выделилась из астрономии и стала самостоятельной математической дисциплиной. К этому времени хорды в тригонометрии были заменены синусами ( отношениями половины хорды к радиусу круга), были введены понятия косинуса и тангенса, а так же составлены таблицы значений тригонометрических функций. Слово «синус» произошло от латинского sinus («перегиб»), которое, в свою очередь, происходит от арабского слова «джива» («тетива лука»). Слово «косинус» – сокращение словосочетания complementi sinus («синус дополнения»), объясняющего тот факт, что cos α равен синусу угла, дополняющего угол до α до π/2, т. е. cos α = sin(π/2- α). Латинское слово tangens переводиться как «касательная» ( «касательная к окружности»).
Идея введения тригонометрических понятий с помощью единичного радиуса получила распространение в X-XI вв.
Идея введения тригонометрических понятий с помощью единичного радиуса получила распространение в X-XI вв.
Слайд 21 Первый научный труд, в котором
тригонометрия утвердилась как самостоятельная ветвь математики, был создан в 1462-1464 гг. немецким астроном и математиком И. Мюллером, известным в истории под псевдонимом Региомонтан (1436-1476). После Региомонтана значительный вклад в тригонометрию внес польский астроном и математик Н. Коперник (1473-1543) , посвятивший этой науке два раздела своего знаменитого труда «Об обращениях небесных тел» (1543). Позже, в сочинениях И. Кеплера (1571-1630), Й. Бюрги (1552-1632), Ф, Виета и других известных математиков, встречаются сложные преобразования тригонометрических выражений и выводятся многие формулы. Интересны, например, рекуррентные формулы, полученные Ф. Виетом: cos mα = 2 cos α cos (m-1)α - cos (m-2)α
cos mα = -2 sin α sin (m-1)α + cos (m-2)α
sin mα = 2 cos α sin (m-1)α - sin (m-2)α
sin mα = 2 sin α cos (m-1)α + sin (m-2)α
Тригонометрическая символика с годами совершенствовалась и лишь в трудах Л. Эйлера в XVIII в. приобрела современный вид, удобный для решения вычислительных задач.
cos mα = -2 sin α sin (m-1)α + cos (m-2)α
sin mα = 2 cos α sin (m-1)α - sin (m-2)α
sin mα = 2 sin α cos (m-1)α + sin (m-2)α
Тригонометрическая символика с годами совершенствовалась и лишь в трудах Л. Эйлера в XVIII в. приобрела современный вид, удобный для решения вычислительных задач.
Слайд 22 Следует отметить, что помимо «плоскостной»
тригонометрии, изучаемой в школе, существует сферическая тригонометрия, являющаяся частью сферической геометрии. Сферическая тригонометрия рассматривает соотношения между сторонами и углами треугольников на сфере , образованных дугами больших кругов сферы. Исторически сферическая тригонометрия возникла из потребностей астрономии фактически раньше тригонометрии на плоскости.
Слайд 24Итог урока.
Мы познакомились с формулами
приведения, учились применять их при
упрощении
выражений, вычислениях.
А теперь
проверь себя, чему и как ты научился
А теперь
проверь себя, чему и как ты научился
Слайд 25Математический диктант.
Продолжи предложение:
Чтобы записать любую из формул приведения, нужно руководствоваться правилами:
В
правой части формулы ставится тот знак, который….
Если в левой части формулы угол равен
π/2±α и 3π/2±α , то…
Если угол равен π±α , то…
Если в левой части формулы угол равен
π/2±α и 3π/2±α , то…
Если угол равен π±α , то…
Слайд 26Продолжи равенство:
2. sin(π/2+α)=
tg(π+α)=
3. cos(3π/2 -α)= sin(3π/2+α)=
4. ctg(π-α)= cos(π/2-α)=
5.Упрости:
sin(3π/2+α) + cos(2π+α)=
cos(π/2+α) + sin(2π-α)=
3. cos(3π/2 -α)= sin(3π/2+α)=
4. ctg(π-α)= cos(π/2-α)=
5.Упрости:
sin(3π/2+α) + cos(2π+α)=
cos(π/2+α) + sin(2π-α)=
Слайд 27Проверим
наши старания.
Продолжи предложение:
Чтобы записать любую из формул приведения, нужно руководствоваться правилами:
В правой части формулы ставится тот знак, который имеет левая часть при условии
0< α<π/2.
Если в левой части формулы угол равен
π/2±α и 3π/2±α , то синус меняется на косинус, тангенс на котангенс и наоборот. Если угол равен π±α , то замены не происходит.
Слайд 282. sin(π/2+α)= cosα tg(π+α)=tg α
3.cos(3π/2 -α)= -sin
α sin(3π/2+α)= -cos α
4. ctg(π-α)= -ctg α cos(π/2-α)=sin α
5.Упрости:
sin(3π/2+α) + cos(2π+α)= 0
cos(π/2+α) + sin(2π-α)= -2sin α
4. ctg(π-α)= -ctg α cos(π/2-α)=sin α
5.Упрости:
sin(3π/2+α) + cos(2π+α)= 0
cos(π/2+α) + sin(2π-α)= -2sin α
Слайд 29Рефлексия.
Результатом своей личной работы считаю, что я ..
А. Разобрался в теории.
В.
Научился решать задачи.
С. Повторил весь ранее изученный материал.
Что вам не хватало на уроке при решении задач?
А. Знаний. Б. Времени. С. Желания.
Д. Решал нормально.
Кто оказывал вам помощь в преодолении трудностей на уроке? А. Одноклассники. Б. Учитель. С. Учебник. Д. Никто.
С. Повторил весь ранее изученный материал.
Что вам не хватало на уроке при решении задач?
А. Знаний. Б. Времени. С. Желания.
Д. Решал нормально.
Кто оказывал вам помощь в преодолении трудностей на уроке? А. Одноклассники. Б. Учитель. С. Учебник. Д. Никто.
Слайд 30Рефлексия.
Результатом своей личной работы считаю, что я ..
А. Разобрался в теории.
В.
Научился решать задачи.
С. Повторил весь ранее изученный материал.
Что вам не хватало на уроке при решении задач?
А. Знаний. Б. Времени. С. Желания.
Д. Решал нормально.
Кто оказывал вам помощь в преодолении трудностей на уроке? А. Одноклассники. Б. Учитель. С. Учебник. Д. Никто.
С. Повторил весь ранее изученный материал.
Что вам не хватало на уроке при решении задач?
А. Знаний. Б. Времени. С. Желания.
Д. Решал нормально.
Кто оказывал вам помощь в преодолении трудностей на уроке? А. Одноклассники. Б. Учитель. С. Учебник. Д. Никто.
СПАСИБО ЗА УРОК!