Садыйкова Энзе Хаертдиновна
2012 год
- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад урока по математике на тему Вписанная и описанная окружности
Содержание
- 1. Презентация урока по математике на тему Вписанная и описанная окружности
- 2. Вписанная окружность.Если все стороны многоугольника касаются окружности,
- 3. Теорема.В любой треугольник можно вписать окружность.Докозательство.Посмотрим треугольник
- 4. В треугольник можно вписать одну и только одну окружностьВ любой четырехугольник нельзя вписать окружность
- 5. В любом описанном четырехугольнике сумма противоположных сторон
- 6. Описанная окружностьЕсли все вершины многоугольника лежат на
- 7. Теорема.Около любого треугольника можно провести описанную окружностьПосмотрим
- 8. Свойство описанной окружности. В любом вписанном четырехугольнике сумма противоположных углов равна 180
- 9. Задача №689У равнобедренного треугольника основание 10 см,
- 10. Задача №690В равнобедренном треугольнике боковая сторона 60
- 11. Задача №691Вписанная в равнобедренный треугольник окружность
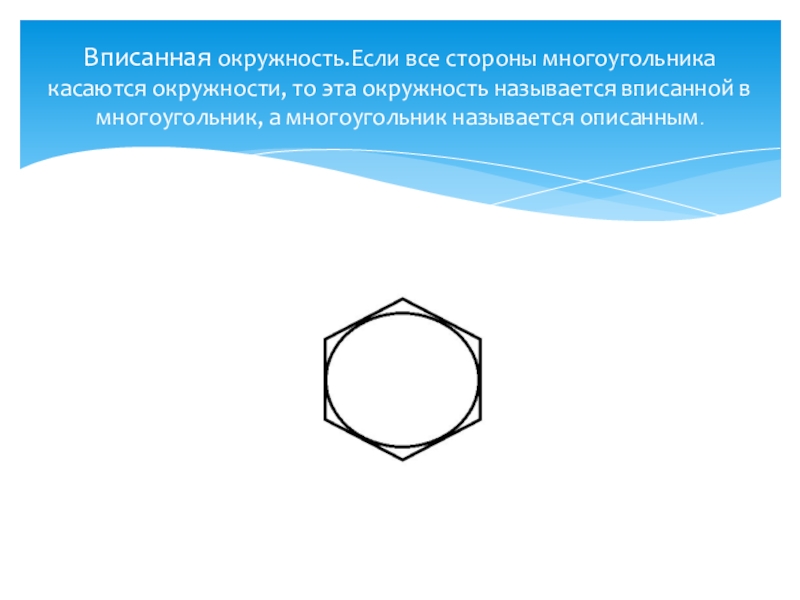
Вписанная окружность.Если все стороны многоугольника касаются окружности, то эта окружность называется вписанной в многоугольник, а многоугольник называется описанным.
Слайд 1Вписанные и описанные окружности. Учительница математики МБОУ «Адаевская ООШ Актанышского муниципального района
РТ»
Слайд 2Вписанная окружность.Если все стороны многоугольника касаются окружности, то эта окружность называется
вписанной в многоугольник, а многоугольник называется описанным.
Слайд 3Теорема.В любой треугольник можно вписать окружность.
Докозательство.Посмотрим треугольник АВС и обозначим через
О точку пересечения биссектрис.Через точку О проводим соответственно на стороны АВ,ВС и СА перпендикуляры ОК,ОL и ОМ.Точка О лежит на равном расстоянии от сторон треугольника АВС, поэтому ОК=ОL=ОМ.Таким образом окружность центром О и радиусом ОК проходит через точки К,L и М. Стороны треугольника АВС касаются окружности в точкахК,L и М, так как они перпендикулярны радиусам ОК, ОL и ОМ. Значит, окружность с центром О и радиусом ОК является вписанной в треугольник АВС.
Слайд 4В треугольник можно вписать одну и только одну окружность
В любой четырехугольник
нельзя вписать окружность
Слайд 5В любом описанном четырехугольнике сумма противоположных сторон равны.
Легко доказывать это свойство.
На рисунке обозначены равные отрезки равными буквами. АВ+СД=а+b +с+d, ВС+АД=а+b+ с+d, поэтому АВ+СД=ВС+АД.
Если у четырехугольника суммы противоположных сторон равны, то можно провести вписанную окружность
Если у четырехугольника суммы противоположных сторон равны, то можно провести вписанную окружность
Слайд 6Описанная окружность
Если все вершины многоугольника лежат на окружности, то эта окружность
называется описанной, а многоугольник-вписанным в окружность. Четырехугольник АВСД является вписанным в окружность с центром О, а четырехугольник АЕСД не является вписанным
Слайд 7Теорема.Около любого треугольника можно провести описанную окружность
Посмотрим любой треугольник АВС. Обозначим
через точку О точку пересечения серединных перпендикуляров и проведем отрезки ОА,ОВ и ОС. Точка О лежит на равном расстоянии от вершин треугольника АВС, поэтому ОА=ОВ=ОС. Итак окружность с центром О и радиусом ОА проходит через три точки треугольника АВС, значит она и есть описанная окружность.
Слайд 8Свойство описанной окружности. В любом вписанном четырехугольнике сумма противоположных углов равна
180
Слайд 9Задача №689
У равнобедренного треугольника основание 10 см, боковые стороны 13 см.
Найти радиус вписанной окружности
Дано: АС=10,АВ=ВС=13
Найти: R=х
Решение: 5: х=13 : (12-х)
13х=5(12-х)
18х=60
х=3 1/3
Дано: АС=10,АВ=ВС=13
Найти: R=х
Решение: 5: х=13 : (12-х)
13х=5(12-х)
18х=60
х=3 1/3
Слайд 10Задача №690
В равнобедренном треугольнике боковая сторона 60 см, центр вписанной окружности
делит высоту, проведенную на основание,считая с вершины как 12:5. Найти основание треугольника.
Дано треугольник АВС. АВ=ВС=60, ВО:ОТ=12:5
Найти АС
Решение: 12:5=60:х
х=25. АС=50
Ответ 50
Дано треугольник АВС. АВ=ВС=60, ВО:ОТ=12:5
Найти АС
Решение: 12:5=60:х
х=25. АС=50
Ответ 50
Слайд 11Задача №691
Вписанная в равнобедренный треугольник окружность в точке касания делит
одну боковую сторону, считая с основания, на отрезки 3см и 4 см.
Найти периметр треугольника.
Дано: АВС –равнобедренный треугольник , АВ=ВС, СМ=3,МВ=4.
Найти: Р.
Решение: СМ=СТ=3, 6+7+7=20
Ответ: 20
Найти периметр треугольника.
Дано: АВС –равнобедренный треугольник , АВ=ВС, СМ=3,МВ=4.
Найти: Р.
Решение: СМ=СТ=3, 6+7+7=20
Ответ: 20