- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад ученика 10 класса Теория узлов
Содержание
- 1. Презентация ученика 10 класса Теория узлов
- 2. Теория узлов
- 3. Слайд 3
- 4. Теория узлов очень важна для широкой науки.
- 5. Узлы, прежде чем стать предметом математической теории,
- 6. Формы узлов
- 7. Математическая проблема-классификация узловВсякий узел, будучи замкнутой кривой
- 8. Узел можно представлять как тонкую запутанную веревку
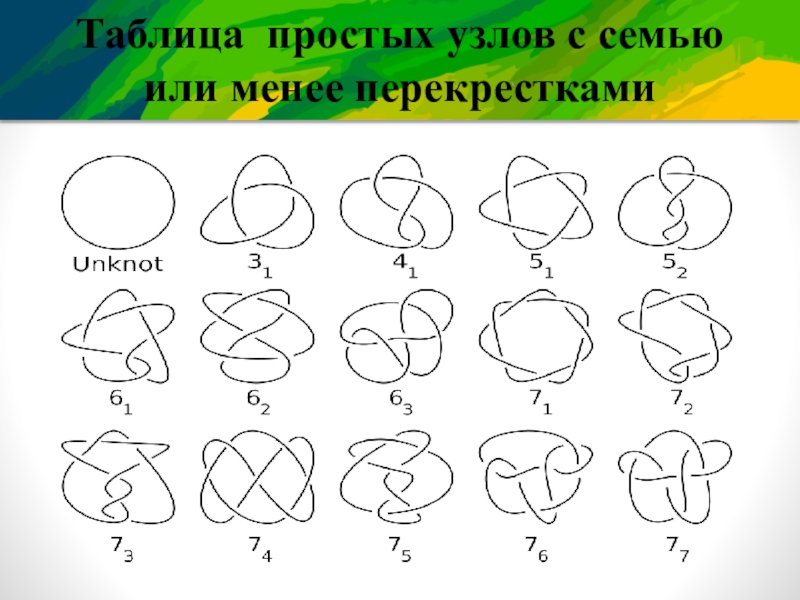
- 9. Таблица простых узлов с семью или менее перекрестками
- 10. Определяем узел, или представление узла, как замкнутую
- 11. Арифметика узловНе только натуральные числа 1, 2,
- 12. Арифметика узловКаждое положительное целое число раскладывается на
- 13. Коммутативность композиции узловТак же как и произведение
- 14. Идея сделать узел моделью атома, предложенная Уильямом
- 15. Интерес к связям между физикой и узлами
Теория узлов
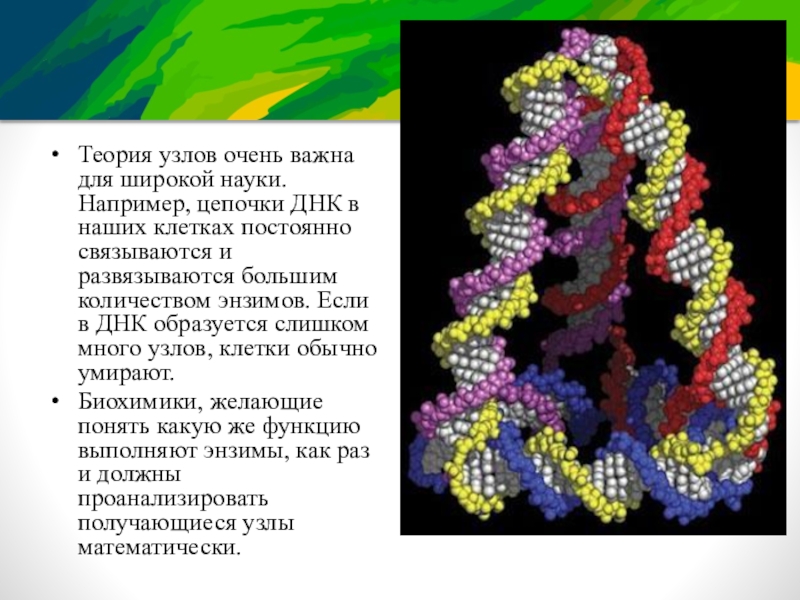
Слайд 4Теория узлов очень важна для широкой науки. Например, цепочки ДНК в
наших клетках постоянно связываются и развязываются большим количеством энзимов. Если в ДНК образуется слишком много узлов, клетки обычно умирают.
Биохимики, желающие понять какую же функцию выполняют энзимы, как раз и должны проанализировать получающиеся узлы математически.
Биохимики, желающие понять какую же функцию выполняют энзимы, как раз и должны проанализировать получающиеся узлы математически.
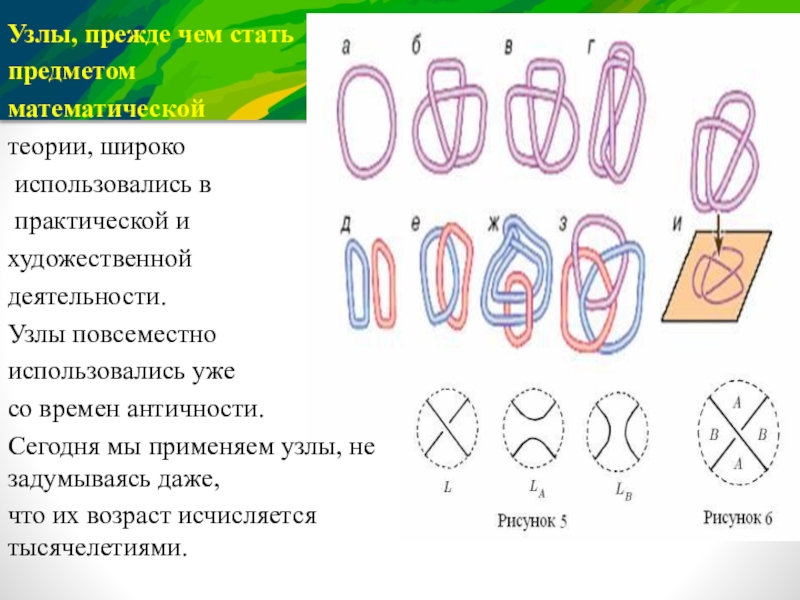
Слайд 5Узлы, прежде чем стать
предметом
математической
теории, широко
использовались в
практической
и
художественной
деятельности.
Узлы повсеместно
использовались уже
со времен античности.
Сегодня мы применяем узлы, не задумываясь даже,
что их возраст исчисляется тысячелетиями.
художественной
деятельности.
Узлы повсеместно
использовались уже
со времен античности.
Сегодня мы применяем узлы, не задумываясь даже,
что их возраст исчисляется тысячелетиями.
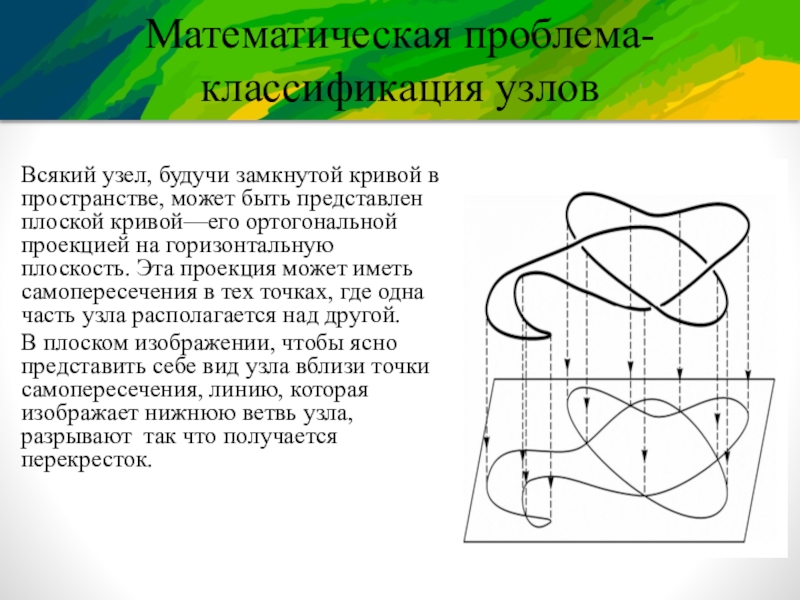
Слайд 7Математическая проблема-классификация узлов
Всякий узел, будучи замкнутой кривой в пространстве, может быть
представлен плоской кривой—его ортогональной проекцией на горизонтальную плоскость. Эта проекция может иметь самопересечения в тех точках, где одна часть узла располагается над другой.
В плоском изображении, чтобы ясно представить себе вид узла вблизи точки самопересечения, линию, которая изображает нижнюю ветвь узла, разрывают так что получается перекресток.
В плоском изображении, чтобы ясно представить себе вид узла вблизи точки самопересечения, линию, которая изображает нижнюю ветвь узла, разрывают так что получается перекресток.
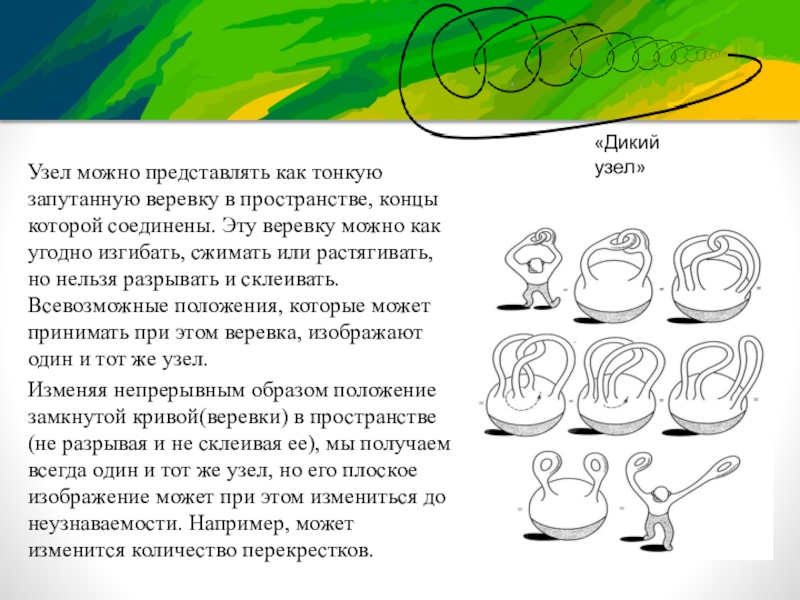
Слайд 8Узел можно представлять как тонкую запутанную веревку в пространстве, концы которой
соединены. Эту веревку можно как угодно изгибать, сжимать или растягивать, но нельзя разрывать и склеивать. Всевозможные положения, которые может принимать при этом веревка, изображают один и тот же узел.
Изменяя непрерывным образом положение замкнутой кривой(веревки) в пространстве (не разрывая и не склеивая ее), мы получаем всегда один и тот же узел, но его плоское изображение может при этом измениться до неузнаваемости. Например, может изменится количество перекрестков.
Изменяя непрерывным образом положение замкнутой кривой(веревки) в пространстве (не разрывая и не склеивая ее), мы получаем всегда один и тот же узел, но его плоское изображение может при этом измениться до неузнаваемости. Например, может изменится количество перекрестков.
«Дикий узел»
Слайд 10Определяем узел, или представление узла, как замкнутую ломаную линию в пространстве.
Собственно
узел есть класс эквивалентности представлений узлов по отношению изотопии, которая определяется следующим образом.
Осуществить элементарную изотопию—значит приложить треугольник ABC к отрезку AB ломаной линии, заменив далее этот отрезок двумя другими сторонами AC∪ CB, либо проделать обратную операцию; разумеется, треугольник не должен иметь общих точек с ломаной, кроме его сторон.
Изотопия есть некоторая последовательность элементарных изотопий .
Осуществить элементарную изотопию—значит приложить треугольник ABC к отрезку AB ломаной линии, заменив далее этот отрезок двумя другими сторонами AC∪ CB, либо проделать обратную операцию; разумеется, треугольник не должен иметь общих точек с ломаной, кроме его сторон.
Изотопия есть некоторая последовательность элементарных изотопий .
Слайд 11Арифметика узлов
Не только натуральные числа 1, 2, 3, 4, 5,... можно
перемножать и раскладывать на простые множители. То же самое можно делать и с другими математическими объектами, в частности, с узлами. При этом их арифметика очень похожа на арифметику натуральных чисел: она тоже обладает коммутативным умножением (которое называется композицией) и теоремой о единственности разложения на «простые узлы». Доказательство этого было получено лишь в 1949 г. немецким математиком Хорстом Шубертом.
Слайд 12Арифметика узлов
Каждое положительное целое число раскладывается на простые множители единственным (с
точностью до порядка сомножителей) образом:
например, 84 = 2 × 2 × 3 × 7;
точно так же и каждый узел является произведением (единственным с точностью до порядка сомножителей) простых узлов.
например, 84 = 2 × 2 × 3 × 7;
точно так же и каждый узел является произведением (единственным с точностью до порядка сомножителей) простых узлов.
Слайд 13Коммутативность композиции узлов
Так же как и произведение чисел, композиция узлов коммутативна
(результат не зависит от порядка множителей):
a # b = b # a.
a # b = b # a.
Слайд 14Идея сделать узел моделью атома, предложенная Уильямом Томсоном почти полтора века
назад, привела к возникновению теории узлов. В совсем недавнем прошлом инварианты узлов стали основанием теорий, имеющих физический характер,—
таких, как топологическая квантовая теория
поля. Где мы находимся сейчас? Можно ли подводить итоги?
таких, как топологическая квантовая теория
поля. Где мы находимся сейчас? Можно ли подводить итоги?
Слайд 15Интерес к связям между физикой и узлами будет возрастать.
Для специалистов по
теории узлов также осталось много работы: например, до сих пор не существует достаточно простого и эффективного алгоритма развязывания, такого, чтобы его можно было перевести на компьютер;
остаются открытыми и многие другие важные проблемы.
Для специалистов в области математической физики, использующих идеи теории узлов, имеется много неисследованных областей.
Исследование всегда начинается с вопроса и с надежды.
остаются открытыми и многие другие важные проблемы.
Для специалистов в области математической физики, использующих идеи теории узлов, имеется много неисследованных областей.
Исследование всегда начинается с вопроса и с надежды.