- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад Тригонометрия вокруг нас
Содержание
- 1. Презентация Тригонометрия вокруг нас
- 2. Актуальность данной темысвязь математики с окружающим миром,
- 3. Целью данной работы является изучение использования тригонометрии
- 4. Слайд 4
- 5. История развития тригонометрииТеория вычислительного приема решения треугольников
- 6. Создается аналитическая теория тригонометрических (круговых)
- 7. Тригонометрия в искусстве cos2 С +
- 8. Художественный музей в Милуоки,СШАСтрунный мост в Иерусалиме , Израиль
- 9. Тригонометрия при инженерно-строительных
- 10. Тригонометрия и тригонометрические функции в
- 11. Для построения
- 12. Движение рыб в воде происходит
- 13. Слайд 13
Слайд 1 Тема : «Тригонометрия
Н. И. Лобачевский
Слайд 2Актуальность данной темы
связь математики с окружающим миром, что позволяет материализовать знания.
Связь математики с окружающим миром позволяет материализовать знания. Это помогает нам лучше понять жизненную необходимость знаний, приобретаемых в школе. Тригонометрические вычисления применяются практически во всех областях геометрии, физики и инженерного дела.
Слайд 3Целью данной работы является изучение использования тригонометрии в различных науках таких
Задачи исследования:
1.Рассмотреть историю возникновения и развития тригонометрии.
2.Показать на конкретных примерах практические приложения тригонометрии в различных науках.
Слайд 4
Изучение взаимосвязи тригонометрии с окружающим миром, определение значения тригонометрии при решении многих практических задач, раскрытие графических возможностей тригонометрических функций дают возможность материализации математических знаний, что позволяет лучше понять жизненную необходимость знаний, приобретаемых при изучении тригонометрии, повышает у школьников интерес к изучению данной темы.
Слайд 5История развития тригонометрии
Теория вычислительного приема решения треугольников и фигур, сводимых к
Клавдий Птолемей
(90 – 168 г н.э)
Пифагор
(580-500 до н.э.)
Слайд 6 Создается аналитическая теория тригонометрических (круговых) функций.
Франсуа Виет
(1540 –
Леонард Эйлер
(1707 – 1783 г. н.э)
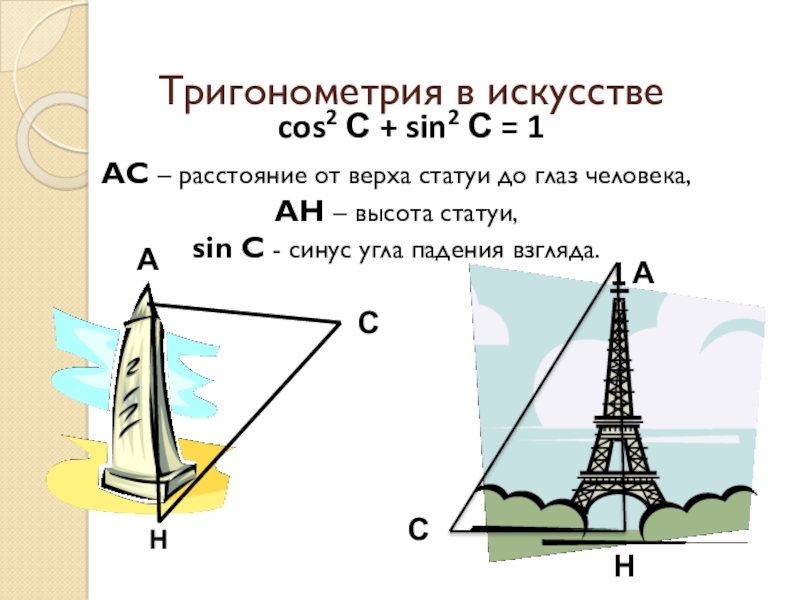
Слайд 7Тригонометрия в искусстве
cos2 С + sin2 С = 1
АС –
АН – высота статуи,
sin С - синус угла падения взгляда.
А
С
Н
А
С
Н
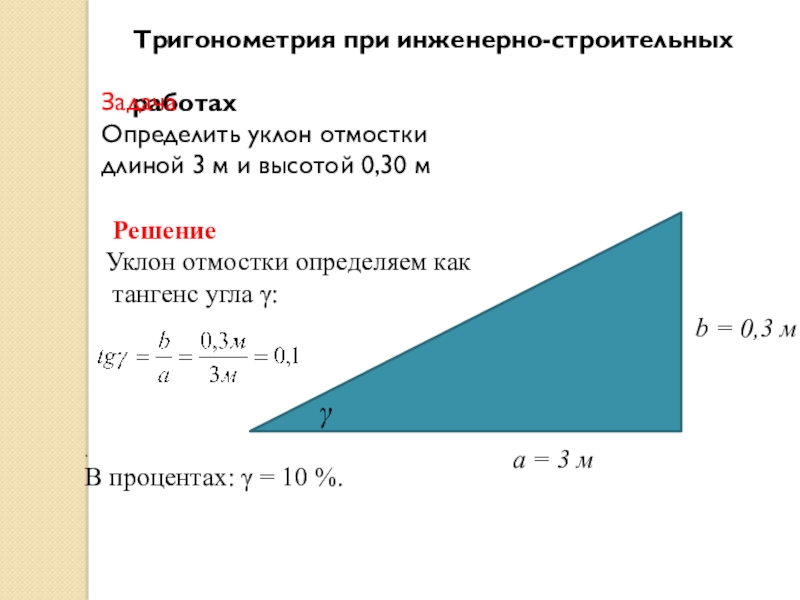
Слайд 9Тригонометрия при инженерно-строительных
а = 3 м
b = 0,3 м
γ
Решение
Уклон отмостки определяем как
тангенс угла γ:
.
В процентах: γ = 10 %.
Задача
Определить уклон отмостки длиной 3 м и высотой 0,30 м
Слайд 10
Тригонометрия и тригонометрические функции в медицине и биологии.
Одно из фундаментальных свойств
Биологические ритмы, биоритмы – это более или менее регулярные изменения характера и интенсивности биологических процессов.
Основной земной ритм – суточный.
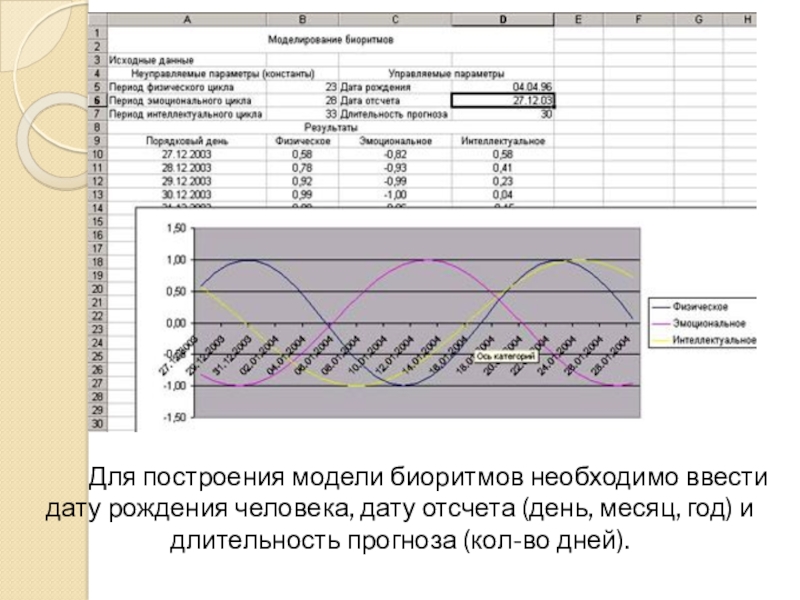
Слайд 11 Для построения модели биоритмов необходимо ввести
Слайд 12 Движение рыб в воде происходит по закону синуса или
При плавании тело рыбы принимает форму кривой, которая напоминает график функции y=tgx.
Слайд 13
Тригонометрические вычисления применяются практически во всех сферах жизнедеятельности людей. Следует отметить их применение в таких областях как: физика, природа, биология, музыка, медицина и многие другие.
Математика имеет аппарат, использование которого при реализации меж предметных связей математики с физикой и другими науками ведет к осознанию единства мира и интеграции научных знаний.