- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад Система подготовки ЕГЭ
Содержание
- 1. Презентация Система подготовки ЕГЭ
- 2. Решать основные задачи по курсам основной
- 3. Курс состоит из следующих блоков: 1. Выражения
- 4. Иррациональные уравненияУравнения с параметрамиФункцииПланиметрия
- 5. Решение иррациональных уравнений.Основные вопросы: 1. Определение иррационального
- 6. Слайд 6
- 7. Слайд 7
- 8. Тренировочный тест
- 9. Основные типы задач для уравнений с параметром.I.
- 10. б) При b ( b
- 11. Решение квадратных уравнений с параметром.При решении таких
- 12. Пример 1. При каких значениях параметра а
- 13. Пример 2: При каком значении параметра m
- 14. Второй способ: решим задачу с применением
- 15. Дробно-рациональные уравнения с параметромПример 1. Решить уравнение:
- 16. Способы нахождения области значения функции:I способ: Область
- 17. IV способ: Использование ограниченности функции.Пример 2. Найти
- 18. V способ: Введение параметра.Пример 3: Найдите множество
- 19. Пример 4: найти область значений функции Решение:
- 20. Биссектриса треугольникаПусть АВС – произвольный треугольник. Проведем
- 21. Задача1: В треугольнике АВС АВ =
Слайд 2 Решать основные задачи по курсам основной и средней школы;
Овладеть
Создать условия для успешной сдачи экзамена выпускниками школы, через оценку собственных возможностей в освоении математического материала на основе закрепления, углубления и расширения знаний, умений и навыков;
Цели:
Слайд 3Курс состоит из следующих блоков:
1. Выражения и преобразования;
2. Уравнения и
3. Функции.
4. Текстовые задачи (проценты, пропорции, прогрессии),
5. Геометрические задачи ( планиметрия, стереометрия).
Слайд 5Решение иррациональных уравнений.
Основные вопросы:
1. Определение иррационального уравнения.
2. Два основных способа
3. Если степень, в которую надо возвести уравнение – четная, то могут возникнуть посторонние корни. Следовательно, необходимо выполнить проверку.
4. Иногда удобнее решать иррациональное уравнение, определив ОДЗ неизвестного и используя равносильные переходы.
Слайд 9Основные типы задач для уравнений с параметром.
I. Решить уравнение при
а) найти все значения переменной а, при которых уравнение имеет решение;
б) найти эти решения при каждом таком а;
в) в ответе указать, что при остальных значениях а, задача не имеет решений.
II. Найти все значения а, при которых уравнение имеет разное количество корней.
Уравнения с параметрами
Слайд 10
б) При b ( b – 1) = 0,
b2 + b – 2 = 0 , т. е. b = - 2, b = 1 . Отсюда следует, что при b = 1 уравнение имеет множество корней.
в) При b ( b – 1) = 0, т. е. b = 0, b = 1 и b2 + b – 2 ≠ 0, т. е. b ≠ - 2, b ≠ 1. Значит, при b = 0 уравнение не имеет корней.
Ответ: при b ≠ 0; b ≠ 1 х = ;
Решение линейных уравнений с параметром.
Решить уравнение: b( b – 1)x = b2 + b – 2.
Решение: Придавая b различные значения, получим уравнения с числовыми коэффициентами. В зависимости от значений параметра мы можем получить три разных случая:
а) При b ( b – 1) ≠ 0, т. е. b ≠ 0, b ≠ 1 уравнение имеет единственный корень:
при b = 1 множество корней х – любое число;
при b = 0 корней нет.
Слайд 11Решение квадратных уравнений с параметром.
При решении таких уравнений необходимо использовать следующие
1. Зависимость количества корней квадратного уравнения от его дискриминанта.
D > 0 ( 2 корня); D = 0 ( 1 корень); D < 0 ( нет корней).
2. Если D > 0, то ах2 + bx + c = a (x – x1) (x – x2).
3. Если D = 0, то левую часть можно представить в виде полного квадрата или выражения, ему противоположного ах2 + bx + c = a (x – x1)2.
4. Если уравнение приведенное, то х1 + х2 = - p, х1 · х2 = q.
5. Если а > 0, D > 0, то уравнение имеет два действительных различных корня
а) b < 0, с > 0 оба корня положительны;
б) b > 0, с > 0 оба корня отрицательны;
в) b < 0 , с < 0 корни противоположны по знаку. Положителен тот
корень, который имеет больший модуль;
г) b > 0, с < 0 корни противоположны по знаку. Отрицателен тот
корень, который имеет больший модуль.
Слайд 12Пример 1. При каких значениях параметра а уравнение ах (ах +
Решение: Преобразуем: а2х2 + 3 ах + 6 = ах2 – 6х;
а2х2 – ах2 + 3 ах + 6х + 6 = 0;
а (а – 1)х2 + 3 (а + 2)х + 6 = 0.
а) уравнение квадратное, если старший коэффициент не равен нулю.
а (а – 1) ≠ 0
а ≠ 0, а ≠ 1.
т. е. уравнение квадратное при всех а, кроме 0 и 1.
б) неполное квадратное уравнение , если b = 0; если с = 0; если b = 0 и с = 0.
3 ( а + 2) = 0 а = - 2.
в) линейное, если коэффициент при х2 равен 0.
а (а – 1) = 0 а = 0, а = 1.
Ответ: при а ≠ 0; 1 уравнение квадратное;
при а = - 2 неполное квадратное;
при а = 0; 1 уравнение линейное.
Слайд 13Пример 2: При каком значении параметра m корни уравнения
(m –
Решение: сравним два способа решения данной задачи. По условию задачи уравнение имеет два корня разных знаков, поэтому имеем графики вида:
Первый способ:(графический) В случае а > 0 парабола направлена вверх и f (0) < 0.
Отсюда составляем систему:
В случае а < 0, парабола направлена вниз и f ( 0) > 0. Тогда система имеет вид:
Совокупность исходных двух систем равносильна неравенству а · f(0) < 0.
Так как а = m – 5 , f (0) = m – 2, имеем квадратное неравенство:
( m – 5)(m – 2) < 0. Решая данное неравенство получаем ответ: (2;5).
Слайд 14 Второй способ: решим задачу с применением теоремы Виета. Так как
Находим приведенный вид уравнения:
Тогда составляем систему неравенств:
Решая данную систему, получаем ответ: (2;5).
Слайд 15Дробно-рациональные уравнения с параметром
Пример 1. Решить уравнение:
Решение: Преобразуем
(m – 2)х = 2m x =
Если m ≠ 2, то x =
Если m = 2, то уравнение корней не имеет.
Найдем значения m, при которых х = 0 и х = 2.
при m = 0.
= 2, 2m = 2m – 4. Данное равенство не выполняется при любом
значении m.
Ответ: если m ≠ 0, m ≠ 2 – единственный корень x =
Если m = 0, m = 2, то уравнение корней не имеет.
Х ≠0, х ≠2
Слайд 16Способы нахождения области значения функции:
I способ: Область значений может быть найдена
II способ: Решается с помощью рассуждений, основанных на анализе свойств функции;
III способ: Найти обратную функцию и её область определения, которая совпадает с областью значений данной функции – «Метод обратных функций».
Пример 1. Найти множество значений функции
Решение: Перейдем к обратной функции
,
,
,
,
х =
Найдем область определения данной функции.
У - 2.
Таким образом, искомое множество есть промежуток [- 2;
Ответ: [- 2;
Слайд 17IV способ: Использование ограниченности функции.
Пример 2. Найти область значений функции
Решение:
=
=
=
Мы знаем, что
.
Ответ:
Слайд 18V способ: Введение параметра.
Пример 3: Найдите множество значений функции
Решение: Переформулируем
имеет хотя бы одно решение».
Перепишем это уравнение. Поскольку
получаем
При а = 1 это уравнение имеет решение х = - 1.
При а ≠ 1 условие существования решения : D
0 или а (4 – 3а)
, т. е. а (3а – 4) ≤ 0, 0 ≤ а ≤
Поскольку особое значение а = 1 входит в этот отрезок,
0
заключаем, что Е(у) =
Ответ:
Слайд 19Пример 4: найти область значений функции
Решение:
При а =
имеет решение.
При а ≠ 2 уравнение принимает вид:
D = 36 – 4(2 – a)(10 – a) = - 4a2 + 48a – 44
D
0, значит, (а – 1)(а – 11)
, а
[1;2)
(2; 11].
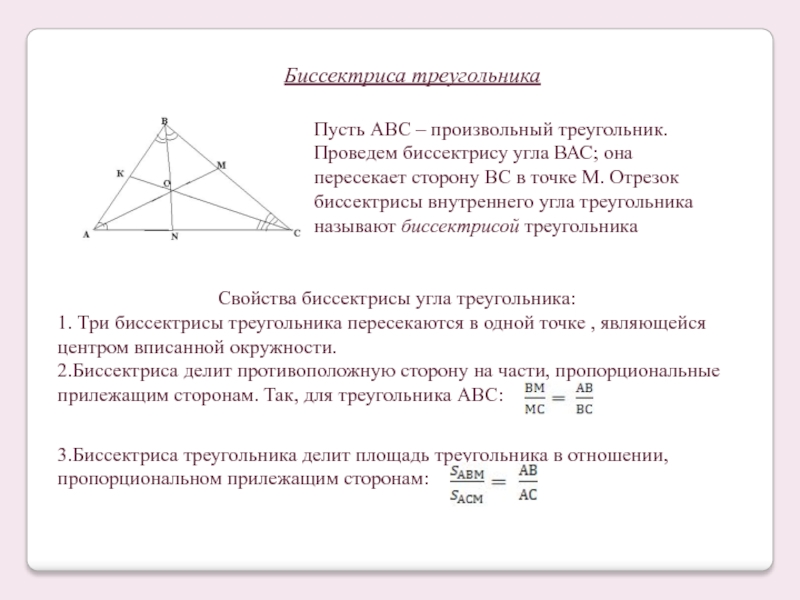
Слайд 20Биссектриса треугольника
Пусть АВС – произвольный треугольник. Проведем биссектрису угла ВАС; она
Свойства биссектрисы угла треугольника:
1. Три биссектрисы треугольника пересекаются в одной точке , являющейся центром вписанной окружности.
2.Биссектриса делит противоположную сторону на части, пропорциональные прилежащим сторонам. Так, для треугольника АВС:
.
3.Биссектриса треугольника делит площадь треугольника в отношении, пропорциональном прилежащим сторонам:
.
Слайд 21Задача1: В треугольнике АВС АВ = 13, ВС = 21,
Решение: АМ = МС = 10.
СО – биссектриса
ВСМ. По свойству биссектрисы имеем:
S =
Так как ВМ – медиана, то SАВМ = SВМС =
SВМС = 63.
СО – биссектриса
ВСМ, то
К обеим частям равенства прибавляем 1.
,
а
SСОМ =
Ответ: