- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад Симметрия в науке и жизни
Содержание
- 1. Презентация Симметрия в науке и жизни
- 2. Симметрия относительно точкиСимметрия относительно точки (центральная симметрия)
- 3. Симметрия относительно прямойСимметрия относительно прямой (осевая симметрия)
- 4. Математика и симметрия. Многочлен от x
- 5. Треугольник Паскаля.Всем известны простые формулы(a + b)2=
- 6. Чудеса треугольника. Рассмотрите треугольник, построенный "относительно" числа
- 7. Чудеса треугольника.В приведенном рисунке красный цвет показывает
- 8. Симметрия многогранников Серьезный шаг в науке
- 9. Симметрия и биологияБлагодаря симметричности, в листьях происходит
- 10. Подавляющее число живых организмов обладает одной из
- 11. Аксиальная симметрия.Это симметричность относительно поворотов на произвольный
- 12. Сферическая симметрия.Опять понятие… Сферический - шарообразный,
- 13. Симметрия кристалловВ старину рудокопы были людьми сугубо
- 14. Кристалл алмазаВ 1850 г. французский физик
- 15. Орнаментальность - первооснова народного декоративного искусства, а симметрия в ней - закономерность организации цветных рисунков.
- 16. Архитектурные сооружения, созданные человеком, в большей своей
- 17. Симметрия воспринимается человеком как проявление закономерности, а
- 18. В чем состоит прочность пирамид?Пирамиды -единственное из
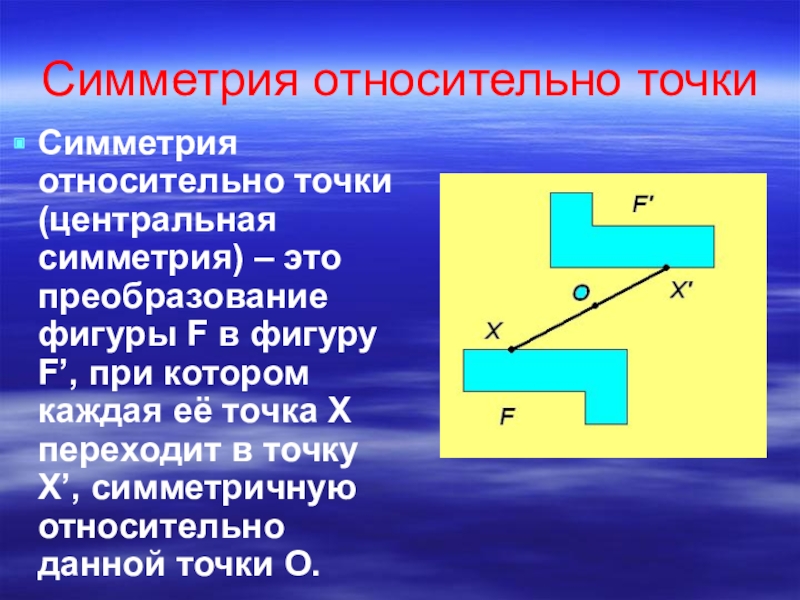
Слайд 2Симметрия относительно точки
Симметрия относительно точки (центральная симметрия) – это преобразование фигуры
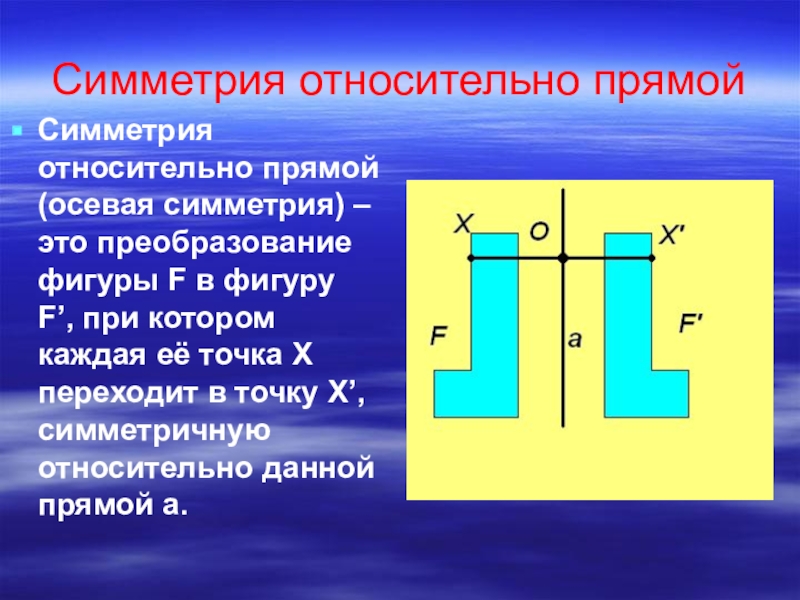
Слайд 3Симметрия относительно прямой
Симметрия относительно прямой (осевая симметрия) – это преобразование фигуры
Слайд 4Математика и симметрия.
Многочлен от x и y называют симметричным,
Приведём важнейшие примеры симметричных многочленов. Как известно из арифметики, при перестановке мест слагаемых сумма не меняется:
x + y = y + x
Теория симметрических многочленов очень проста и позволяет решать многие алгебраические задачи: решение иррациональных уравнений, доказательство тождеств и неравенств, разложение на множители, решение систем алгебраических уравнений, и т. д. С помощью теории симметрических многочленов решение этих задач заметно упрощается и, что самое главное, проводится стандартным приёмом.
Слайд 5Треугольник Паскаля.
Всем известны простые формулы
(a + b)2= a2+2ab + b2
(a
Устройство треугольника Паскаля: каждое число равно сумме двух расположенных над ним чисел. Все элементарно, но сколько в этом таится чудес.
Слайд 6Чудеса треугольника.
Рассмотрите треугольник, построенный "относительно" числа 7, то есть, числа,
нарисованы черным цветом,
делящиеся – белым.
Попробуйте увидеть закономерности.
Слайд 7Чудеса треугольника.
В приведенном рисунке красный цвет показывает четности числа, зеленый -
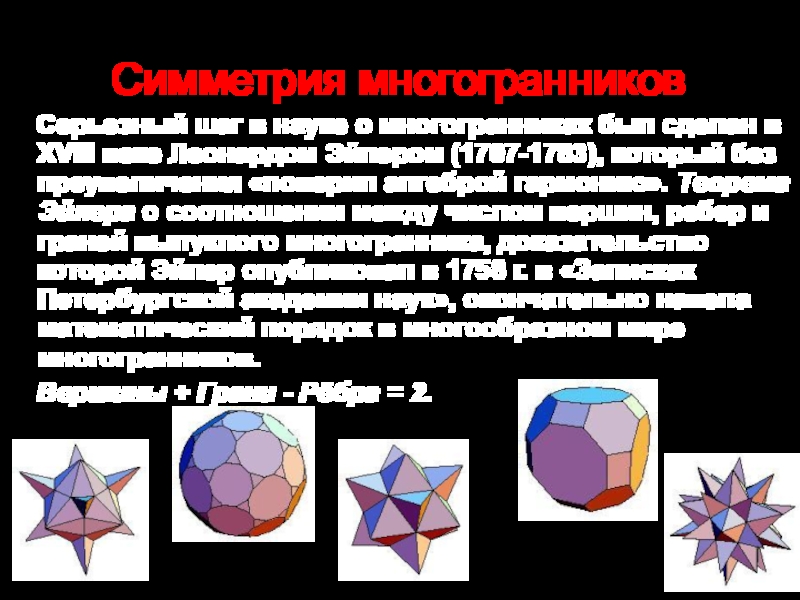
Слайд 8Симметрия многогранников
Серьезный шаг в науке о многогранниках был сделан
Вершины + Грани - Рёбра = 2.
Слайд 9Симметрия и биология
Благодаря симметричности, в листьях происходит равномерный процесс фотосинтеза и
Листья многих растений обладают свойством симметричности относительно центральной жилки.
При нарушении симметрии листьев растение не в состоянии полноценно развиваться, в результате чего происходит отмирание этих листьев.
Слайд 10Подавляющее число живых организмов обладает одной из трех ее видов симметрии:
В случае несимметричного развития животного поворот в одну из сторон был бы для него затруднен и естественным для животного стало бы не прямолинейное, а круговое движение. Хождение же по кругу рано или поздно закончится трагически для животного.
Жук - навозник
Жук - усач
Слайд 11Аксиальная симметрия.
Это симметричность относительно поворотов на произвольный угол вокруг какой-либо оси.
В
Такая симметрия характерна для многих стрекающих, а также для большинства иглокожих.
Слайд 12Сферическая симметрия.
Опять понятие…
Сферический - шарообразный, шаровидный.
Делаем вывод…
Сферическая
Слайд 13Симметрия кристаллов
В старину рудокопы были людьми сугубо практическими. Они не забивали
Для полезных (на их взгляд) минералов они подыскивали наглядные и запоминающиеся имена. Можно никогда не видеть копьевидного колчедана, но без особого труда представить его себе по названию..
Когда же минералогия превратилась в науку, было открыто великое множество пород и минералов. И при этом все чаще возникали трудности с изобретением для них наименований.
Музеи пополнялись грандиозными коллекциями камней, которые становились уже необозримыми.
Слайд 14 Кристалл алмаза
В 1850 г. французский физик Опост Браве (1811—1863) выдвинул
Слайд 15Орнаментальность - первооснова народного декоративного искусства, а симметрия в ней -
Слайд 16Архитектурные сооружения, созданные человеком, в большей своей части симметричны. Они приятны
Во-первых, все мы с вами живем в симметричном мире, который обусловлен условиями жизни на планете Земля, прежде всего существующей здесь гравитацией. И, скорее всего, подсознательно человек понимает, что симметрия это форма устойчивости, а значит существования на нашей планете. Поэтому в рукотворных вещах он интуитивно стремится к симметрии. Во-вторых, окружающие человека люди, растения, животные и вещи симметричны. Однако при ближайшем рассмотрении оказывается, что природные объекты (в отличие от рукотворных) только почти симметричны. Но это не всегда воспринимает глаз человека. Глаз человека привыкает видеть симметричные объекты. Они воспринимаются как гармоничные и совершенные.
Симметрия в архитектуре
Слайд 17Симметрия воспринимается человеком как проявление закономерности, а значит внутреннего порядка. Внешне
Слайд 18В чем состоит прочность пирамид?
Пирамиды -единственное из , сохранившееся
Пирамида, имеющая в основании правильный квадрат,- уникальная в истории архитектуры форма, в которой понятия конструкции (геометрической основы) и композиции (образной целостности) оказываются тождественными. Это вершина искусства геометрического стиля.
Простота и ясность формы пирамиды выводят ее из исторического времени. Именно так следовало бы прочесть крылатую фразу: <Все на свете боится времени, а время боится пирамид>.