- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад Решение задач по геометрии
Содержание
- 1. Презентация: Решение задач по геометрии
- 2. Некоторые теоремы Три медианы треугольника пересекаются в
- 3. Теорема о пропорциональности отрезков, высекаемых на сторонах
- 4. Задача 1.Периметр прямоугольного треугольника равен 60 см.
- 5. Задача 2.В треугольнике АВС сторона АВ=6, сторона
- 6. По теореме о пропорциональности отрезков, высекаемых на
- 7. Задача 3.Через точку, взятую внутри треугольника, проведены
- 8. Проводим аналогичные рассуждения для треугольников DQO и
- 9. Задача 4.На сторонах АВ и ВС треугольника
- 10. Задача 5.На стороне АС треугольника АВС Взята
- 11. Складывая почленно равенства (1) и (2), получаем:Находим
- 12. Задача
- 13. Задача
- 14. Слайд 14
- 15. Используемая литература 1. В.А.Кокотушкин, Н.Г.Панфилов
Слайд 1Решение
задач по геометрии
Подготовка к ЕГЭ
Планиметрия
Учитель математики
МАОУ СОШ № 13
Слайд 2Некоторые теоремы
Три медианы треугольника пересекаются в одной точке, которая делит
Три биссектрисы внутренних углов треугольника пересекаются в одной точке. Точка пересечения биссектрис является центром вписанной окружности.
Биссектриса внутреннего угла треугольника делит противоположную сторону на части, пропорциональные прилежащим сторонам.
Три высоты треугольника пересекаются в одной точке, называемой ортоцентром.
Три серединных перпендикуляра сторон треугольника пересекаются в одной точке, являющейся центром описанной окружности.
Слайд 3Теорема о пропорциональности отрезков, высекаемых на сторонах угла параллельными прямыми. Стороны
Признаки подобия треугольников. Два треугольника подобны, если выполнено хотя бы одно из условий:
два угла одного треугольника равны двум углам другого треугольника;
две стороны одного треугольника пропорциональны двум сторонам другого треугольника, а углы, заключённые между пропорциональными сторонам, равны;
три стороны одного треугольника пропорциональны трём сторонам другого треугольника.
Свойства подобных треугольников. В подобных треугольниках
сходственные элементы (например, медианы, высоты, периметры,
Радиусы вписанной и описанной окружностей и др.) относятся как
сходственные стороны, и это отношение равно коэффициенту подобия.
Площади подобных треугольников относятся как квадраты сходственных
сторон, т.е. отношение площадей подобных треугольников равно
квадрату коэффициента подобия.
Слайд 4Задача 1.
Периметр прямоугольного треугольника равен 60 см. Найти его стороны, если
Решение.
Составим и решим систему:
Решая систему, находим стороны: 15 см, 20 см, 25 см.
Ответ: 15 см, 20 см, 25 см.
Слайд 5Задача 2.
В треугольнике АВС сторона АВ=6, сторона АС=9. Из вершины В
Решение.
Пусть D –середина биссектрисы AL, К – точка пересечения BD и АС. Проведём LM//ВК. Пусть АК=х.
По теореме Фалеса АК=КМ, поэтому КМ=х. По свойству биссектрисы BL:LC=АВ:АС=6:9=2:3.
Слайд 6По теореме о пропорциональности отрезков, высекаемых на сторонах угла параллельными прямыми,
Т.о., Тогда
Ответ: 2:5
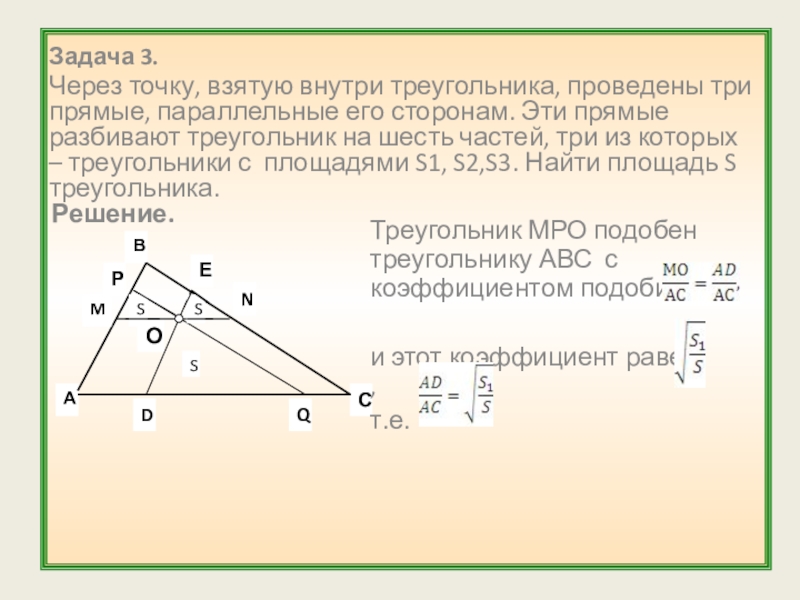
Слайд 7Задача 3.
Через точку, взятую внутри треугольника, проведены три прямые, параллельные его
Решение.
Треугольник МРО подобен треугольнику АВС с коэффициентом подобия
и этот коэффициент равен ,
т.е.
Слайд 8Проводим аналогичные рассуждения для треугольников DQO и OEN, получаем:
Складываем эти равенства и, учитывая, что AD+DQ+QC=AC,
получаем: .
Отсюда
Ответ:
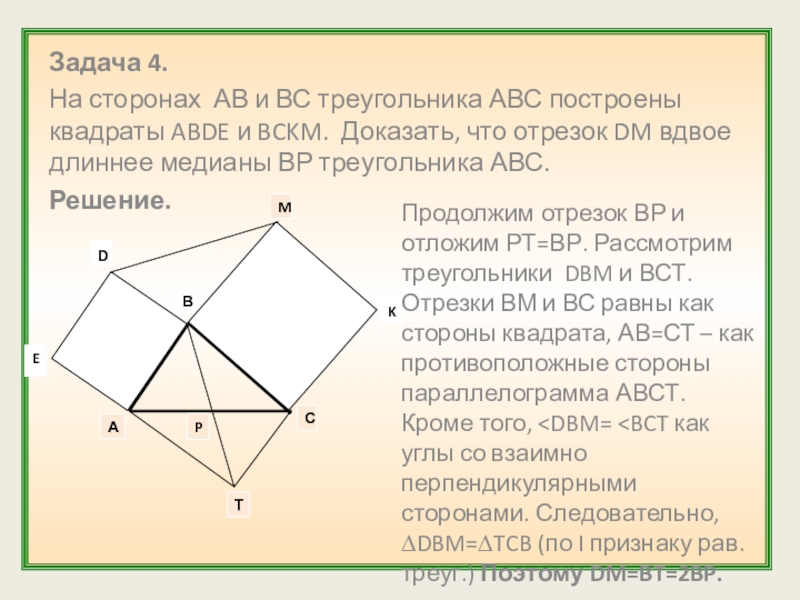
Слайд 9Задача 4.
На сторонах АВ и ВС треугольника АВС построены квадраты ABDE
Решение.
Продолжим отрезок ВР и отложим РТ=ВР. Рассмотрим треугольники DBM и ВСТ. Отрезки ВМ и ВС равны как стороны квадрата, АВ=СТ – как противоположные стороны параллелограмма АВСТ. Кроме того,
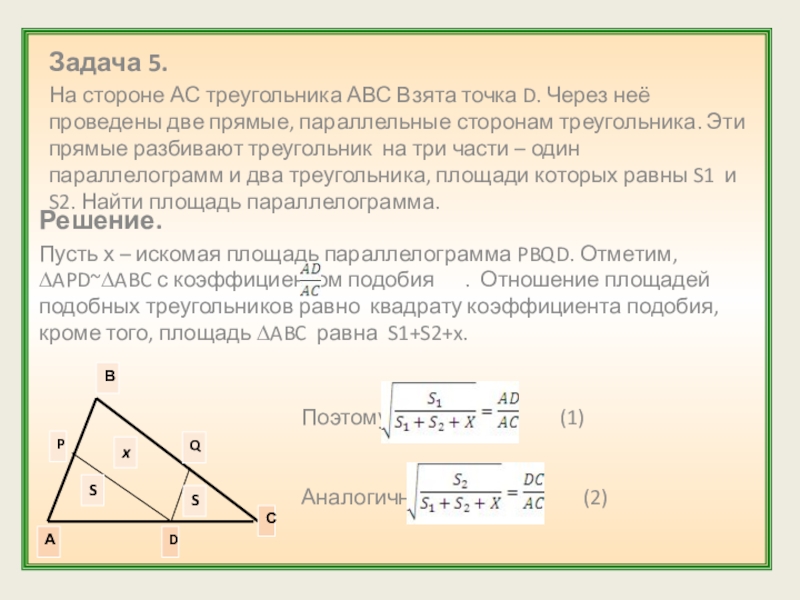
Слайд 10Задача 5.
На стороне АС треугольника АВС Взята точка D. Через неё
Решение.
Пусть х – искомая площадь параллелограмма PBQD. Отметим, ∆APD~∆ABC с коэффициентом подобия . Отношение площадей подобных треугольников равно квадрату коэффициента подобия, кроме того, площадь ∆ABC равна S1+S2+x.
Поэтому (1)
Аналогично (2)
Слайд 11Складывая почленно равенства (1) и (2), получаем:
Находим х из данного равенства
Ответ:
Слайд 12
Задача 6.
Серединный перпендикуляр к гипотенузе
Решение. b
Пусть АВ = 2х. ∆АМР ~ ∆NВР
(по двум углам: <АМР = <В и
Поэтому , откуда .
Итак, АВ = 2
Ответ: 2
Слайд 13
Задача 7.
В треугольнике АВС сторона
Решение.
Отметим (Рис. 1), что ВС = BD + DC. Так как точка О лежит на биссектрисах углов треугольника АВС,
то , откуда (1)
Рис. 1
Слайд 14
Проведём
Обозначим . Тогда из равенств (1) и (2) получим систему
уравнений
Ответ:
Рис. 2