- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад проекта по математике Удивительный мир фракталов
Содержание
- 1. Презентация проекта по математике Удивительный мир фракталов
- 2. МКОУ «Захаровская СШ» Клетского района Волгоградской областиАвторы:
- 3. Холодная и сухая! Геометрию часто называют холодной
- 4. Новая геометрия!С огромной для нас радостью мы
- 5. Актуальность проекта: Роль фракталов в современном
- 6. Гипотеза исследования:Фрактальная геометрия – современная, очень интересная
- 7. Цель проекта:Изучить теорию фракталов для создания научной
- 8. Задачи проекта:Познакомиться с историей возникновения и развития
- 9. Этапы работы:Сбор необходимой информации: использование сети Интнрнет,
- 10. История фракталов
- 11. Бенуа Мандельброт «Фрактальная геометрия природы» 1977год
- 12. «Fractional» - дробный. Фрактал - геометрическая фигура,
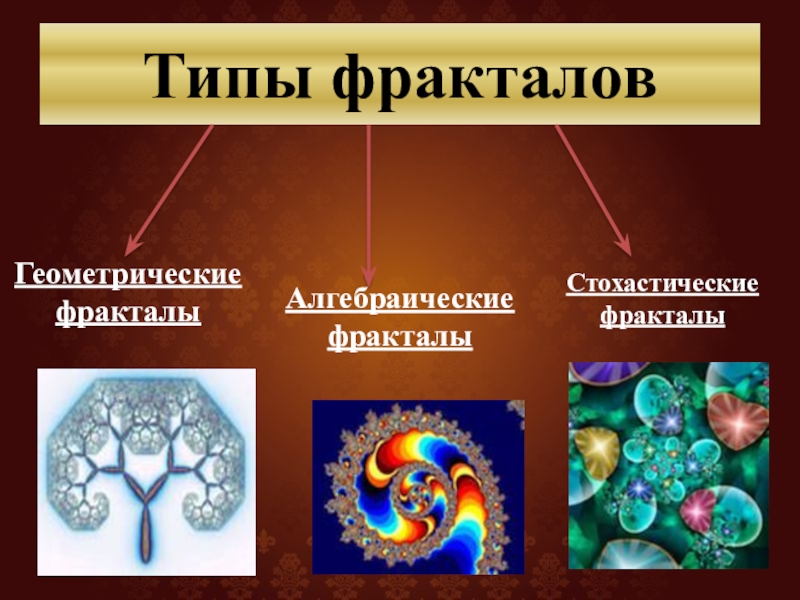
- 13. Типы фракталовГеометрические фракталыАлгебраические фракталыСтохастические фракталы
- 14. Геометрические фракталы
- 15. Самые наглядныеГеометрические фракталы по-другому называют классическими. Они
- 16. Снежинка Коха Изобретена в 1904 годнемецким математиком
- 17. Пятиугольник Дюрера Фрактал выглядит как связка
- 18. Салфетка СерпинскогоВ 1915 году польский математик Вацлав
- 19. Кривая драконаИзобретена итальянским математиком Джузеппе Пеано. Берется
- 20. Ковер Серпинского Берется квадрат , разбивается на
- 21. Алгебраические фракталы
- 22. Странная фигураСвое название они получили за то,
- 23. Множество МандельбротаМножество Мандельброта, которое было построено Бенуа
- 24. Множество ЖюлиаМножество Жулиа было изобретено французским математиком
- 25. Бассейны НьютонаБассейны Ньютона, фракталы Ньютона – разновидность
- 26. Стохастические фракталы
- 27. «Предположение»Термин "стохастичность" происходит от греческого слова, обозначающего
- 28. Плазма Типичный представитель данного класса фракталов
- 29. «Великая книга Природы написана на языке геометрии» Галилео Галилей
- 30. Фракталы вокруг нас
- 31. В живой природе.КораллыМорские звезды и ежи.Морские раковины.Цветы
- 32. В неживой природе.Границы географических объектов.Береговые линии.Горные хребты.СнежинкиОблака, молнии.Морозные узоры на окнахКристаллы, сталактиты,сталагмиты.
- 33. Природные фракталы. Почти все природные образования
- 34. Морские фракталы.Осьминог – морское придонное животное из
- 35. Зеленый фракталЗеленый фрактал – листья папоротника.Листья папоротника
- 36. Фрактал, от которого плачут Лук – фрактал,
- 37. Яркий пример фракталаЯрким примером фрактала в природе
- 38. Типичный фракталЦветная капуста - типичный фрактал.Рассмотрим строение
- 39. Сувенир «Матрешка»Фрактальная игрушка Матрешка -
- 40. Человек – это фрактал!Рождается ребенок, растет, становится взрослым и этот процесс сопровождается принципом «самоподобия», фрактальностью.
- 41. «Математика представляет собой собрание выводов, которые могут быть применены к чему угодно» Бертран Рассел
- 42. Применение фракталов
- 43. Фракталы в литературеУ попа была собака, он ее любил.Она съела
- 44. Фракталы в литературе«Вот дом.Который построил Джек.А вот
- 45. Фракталы в телекоммуникацииДля передачи данных на расстояния
- 46. Организм человекаНа данное время фракталы находят и
- 47. Фракталы внутри насБронхиальные пути в легких. Фрактальная размерность 1.07Артерии. Фрактальная размерность 2.7
- 48. Фракталы в медицине Теория фракталов применятся для
- 49. Фракталы в медицине Рентгеновские снимки обработанные с
- 50. Фракталы в медицинеЕще одна область активного применения
- 51. Фракталы в архитектуреФрактальный принцип развития природных и
- 52. Фракталы в дизайнеДизайнеры со всего мира начали
- 53. Фракталы в мебели.Дизайнер Такеси Миякава в детстве
- 54. Фракталы в экономике Последнее время фракталы
- 55. Фракталы в играх Сегодня в
- 56. Фракталы в киноВ кино для создания различных
- 57. Электронная музыка Зрелищность фрактальной анимации с
- 58. Естественные наукиОчень часто фракталы применяются в геологии
- 59. Фракталы в физике В физике фракталы
- 60. Изучение турбулентностиИзучение турбулентности в потоках очень хорошо
- 61. Фракталы в механике жидкостейПри помощи фракталов также можно смоделировать языки пламени.
- 62. Фракталы в биологии В биологии они применяются
- 63. Фракталы для домохозяек Фрактальные сережки Фрактальное печенье
- 64. «Мир устроен не только причудливей, чем мы
- 65. Фрактальная графика
- 66. Слайд 66
- 67. Слайд 67
- 68. Слайд 68
- 69. Слайд 69
- 70. Слайд 70
- 71. Слайд 71
- 72. Слайд 72
- 73. Слайд 73
- 74. Практическая часть проекта
- 75. Результат работыСоздали научную работу «Путешествие в мир фракталов»
- 76. Автор: Рыжкова Ангелина
- 77. Автор: Фомина Ирина.
- 78. Наши достиженияПриняли участие с работой « Путешествие
- 79. Гимн фракталам!Можно с полной уверенностью сказать об
- 80. Результаты работы:Познакомились с историей возникновения и развития
МКОУ «Захаровская СШ» Клетского района Волгоградской областиАвторы: Фомина Ирина – 9 классРыжкова Ангелина – 9 классРуководители:Могутова Татьяна МихайловнаДерюшкина Оксана Валерьевна
Слайд 2МКОУ «Захаровская СШ» Клетского района Волгоградской области
Авторы:
Фомина Ирина –
9 класс
Рыжкова Ангелина – 9 класс
Руководители:
Могутова Татьяна Михайловна
Дерюшкина Оксана Валерьевна
Рыжкова Ангелина – 9 класс
Руководители:
Могутова Татьяна Михайловна
Дерюшкина Оксана Валерьевна
Слайд 3Холодная и сухая!
Геометрию часто называют холодной и сухой.
Одна из
причин заключается в ее неспособности описать все то, что окружает нас: форму облака, горы, дерева или берега моря.
Слайд 4Новая геометрия!
С огромной для нас радостью мы узнали, что в современном
мире существует
новая геометрия – геометрия фракталов.
новая геометрия – геометрия фракталов.
Слайд 5Актуальность проекта:
Роль фракталов в современном мире достаточно велика.
Убедительных аргументов
в пользу актуальности изучения фракталов является широта области их применения.
Слайд 6Гипотеза исследования:
Фрактальная геометрия – современная, очень интересная область человеческого познания. Появление
фрактальной геометрии есть свидетельство продолжающейся эволюции человека и расширения его способов познания мира.
Слайд 7Цель проекта:
Изучить теорию фракталов для создания научной работы «Удивительный мир фракталов»
и разработки и реализации на компьютере алгоритмов рисования фракталов на плоскости.
.
Слайд 8Задачи проекта:
Познакомиться с историей возникновения и развития фрактальной геометрии;
Изучить виды фракталов,
их применение в современном мире.
Выполнить программы создания фракталов на языках программирования Pascal и Logo
Создать научную работу о фракталах, опубликовать ее в сети Интернет.
Создать брошюры «Фракталы вокруг нас»,
«Применение фракталов».
Выполнить программы создания фракталов на языках программирования Pascal и Logo
Создать научную работу о фракталах, опубликовать ее в сети Интернет.
Создать брошюры «Фракталы вокруг нас»,
«Применение фракталов».
Слайд 9Этапы работы:
Сбор необходимой информации: использование сети Интнрнет, книг, публикаций по данной
теме.( 2 недели)
Сортировка информации по темам: систематизация и определение порядка написания работы. Выполнение этапа заняло 2 недели.
Составление текстовой работы: написание текста, частичное оформление систематизированной информации. Заняло один месяц.
Создание презентации: сжатие систематизированных сведений, определение структуры презентации, её создание и оформление и проходило в течении месяца.
Изучение программы создания фракталов и создание собственных фракталов на языках программирования Pascal и Logo (до сегодняшнего дня)
Сортировка информации по темам: систематизация и определение порядка написания работы. Выполнение этапа заняло 2 недели.
Составление текстовой работы: написание текста, частичное оформление систематизированной информации. Заняло один месяц.
Создание презентации: сжатие систематизированных сведений, определение структуры презентации, её создание и оформление и проходило в течении месяца.
Изучение программы создания фракталов и создание собственных фракталов на языках программирования Pascal и Logo (до сегодняшнего дня)
Слайд 12«Fractional» - дробный.
Фрактал -
геометрическая фигура, составленная из нескольких частей,
каждая из которых подобна всей фигуре целиком. Небольшая часть фрактала содержит информацию обо всем фрактале.
Слайд 15Самые наглядные
Геометрические фракталы по-другому называют классическими.
Они являются самыми наглядными,
так как обладают так называемой жесткой самоподобностью, не изменяющейся при изменении масштаба.
Независимо от того, насколько вы приближаете фрактал, вы видите всё тот же узор.
Независимо от того, насколько вы приближаете фрактал, вы видите всё тот же узор.
Геометрические фракталы по-другому называют классическими, детерминированными или линейными. Они являются самыми наглядными, так как обладают так называемой жесткой самоподобностью, не изменяющейся при изменении масштаба. Это значит, что, независимо от того, насколько вы приближаете фрактал, вы видите всё тот же узор.
Геометрические фракталы по-другому называют классическими, детерминированными или линейными. Они являются самыми наглядными, так как обладают так называемой жесткой самоподобностью, не изменяющейся при изменении масштаба. Это значит, что, независимо от того, насколько вы приближаете фрактал, вы видите всё тот же узор.
Слайд 16Снежинка Коха
Изобретена в 1904 год
немецким математиком
Хельге фон Кохом.
Для
её построения берется единичный отрезок, делится на три равные части и среднее звено заменяется равносторонним треугольником без этого звена. На следующем шаге повторяем операцию для каждого из четырёх получившихся отрезков. В результате бесконечного повторения данной процедуры получается фрактальная кривая.
Ее фрактальная размерность равна 1.261859507
Ее фрактальная размерность равна 1.261859507
Слайд 17Пятиугольник Дюрера
Фрактал выглядит как связка пятиугольников, сжатых вместе. Фактически
он образован при использовании пятиугольника в качестве инициатора и равнобедренных треугольников, отношение большей стороны к меньшей в которых в точности равно так называемой золотой пропорции Эти треугольники вырезаются из середины каждого пятиугольника, в результате чего получается фигура, похожая на 5 маленьких пятиугольников, приклеенных к одному большому.
Слайд 18Салфетка Серпинского
В 1915 году польский математик
Вацлав Серпинский
придумал занимательный объект.
Для его построения берётся сплошной равносторонний треугольник. На первом шаге из центра удаляется перевернутый равносторонний треугольник. На втором шаге удаляется три перевернутых треугольника из трёх оставшихся треугольников и т.д
.
Слайд 19Кривая дракона
Изобретена итальянским математиком
Джузеппе Пеано.
Берется отрезок прямой. На каждом
шаге отрезок заменяется на ломаную из двух равных отрезков, составляющих прямой угол между собой. Направление вершины угла определяется так, чтобы никакие два соседних отрезка в образовавшейся фигуре не лежали на одной прямой.
.
.
Слайд 20Ковер Серпинского
Берется квадрат , разбивается на девять равных квадратов ,
средний из которых выбрасывается, а с остальными повторяется та же операция до бесконечности.
Слайд 22Странная фигура
Свое название они получили за то, что их строят на
основе алгебраических формул:
На экран выводится точка определенного цвета.
Результатом оказывается странная фигура, в которой прямые линии переходят в кривые
Практически каждая точка на экране компьютера как отдельный фрактал
На экран выводится точка определенного цвета.
Результатом оказывается странная фигура, в которой прямые линии переходят в кривые
Практически каждая точка на экране компьютера как отдельный фрактал
Слайд 23Множество Мандельброта
Множество Мандельброта, которое было построено Бенуа Мандельбротом.
Это первая ассоциация,
возникающая у людей, когда они слышат слово фрактал. Этот фрактал, напоминающий чесальную машину с прикрепленными к ней пылающими древовидными и круглыми областями, генерируется простой формулой Zn+1=Zna+C, г
Слайд 24Множество Жюлиа
Множество Жулиа было изобретено французским математиком Гастоном Жулиа.
Множества Жулиа можно
сгенерировать используя эти точки в качестве начальных значений в уравнении
Z=ZІ+C.
Z=ZІ+C.
Слайд 25Бассейны Ньютона
Бассейны Ньютона, фракталы Ньютона – разновидность алгебраических фракталов.
Области с фрактальными
границами проявляются при приближенном нахождении корней нелинейного уравнения на комплексной плоскости
Слайд 27«Предположение»
Термин "стохастичность" происходит от греческого слова, обозначающего "предположение".
Эти фракталы используются
при моделировании рельефов местности и поверхности морей, процесса электролиза
Получаются объекты очень похожие на природные - несимметричные деревья, изрезанные береговые линии и т.д.
Получаются объекты очень похожие на природные - несимметричные деревья, изрезанные береговые линии и т.д.
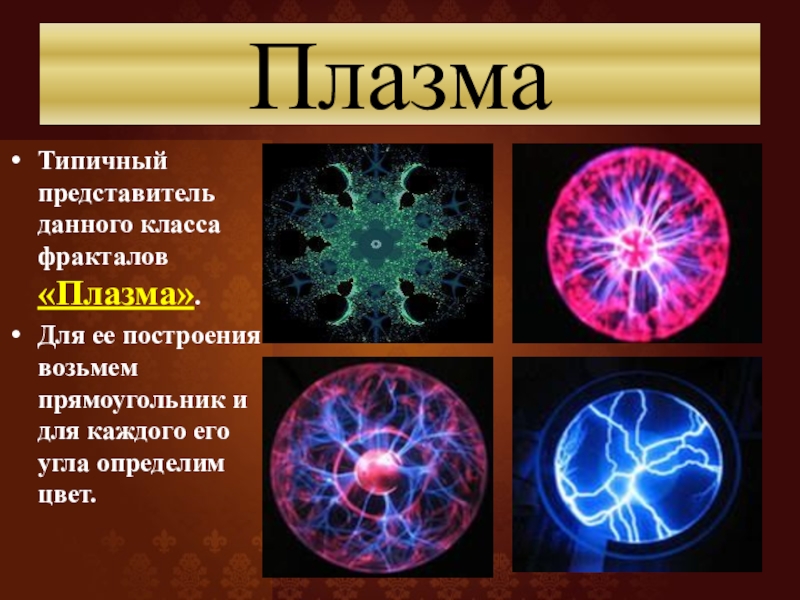
Слайд 28
Плазма
Типичный представитель данного класса фракталов «Плазма».
Для ее построения возьмем прямоугольник
и для каждого его угла определим цвет.
Слайд 31В живой природе.
Кораллы
Морские звезды и ежи.
Морские раковины.
Цветы и растения (брокколи, капуста)
Кроны
деревьев и листья растений.
Плоды (ананас)
Кровеносная система и бронхи у людей и животных
Плоды (ананас)
Кровеносная система и бронхи у людей и животных
Слайд 32В неживой природе.
Границы географических объектов.
Береговые линии.
Горные хребты.
Снежинки
Облака, молнии.
Морозные узоры на окнах
Кристаллы,
сталактиты,сталагмиты.
Слайд 33Природные фракталы.
Почти все природные образования : кроны деревьев, облака,
горы, береговые линии имеют фрактальную структуру.
Если посмотреть на фрактальный объект в целом, затем на его часть в увеличенном масштабе, потом на часть этой части ,
то нетрудно увидеть, что они выглядят одинаково.
.
Если посмотреть на фрактальный объект в целом, затем на его часть в увеличенном масштабе, потом на часть этой части ,
то нетрудно увидеть, что они выглядят одинаково.
.
В природе фрактальными свойствами обладают многие объекты, например: кроны деревьев, облака, горные хребты, берега рек, озер, морей.
Слайд 34Морские фракталы.
Осьминог – морское придонное животное из отряда головоногих.
Фрактальное строение
имеют его тела и присоски на всех восьми щупальцах этого животного.
.
Еще одни типичнейшим
Представителем фрактального подводного мира является коралл.
В природе известно свыше 3500 разновидностей кораллов
Слайд 35Зеленый фрактал
Зеленый фрактал – листья папоротника.
Листья папоротника имеют форму фрактальной фигуры
— они самоподобны.
Слайд 36Фрактал, от которого плачут
Лук – фрактал, который заставляет плакать.
Конечно,
фрактал он незамысловатый: обычные окружности разного диаметра, можно даже сказать примитивный фрактал.
Слайд 37Яркий пример фрактала
Ярким примером фрактала в природе является «Романеску», она же
«романская брокколи»
или «цветная коралловая капуста». Почки этой капусты растут по логарифмической спирали
или «цветная коралловая капуста». Почки этой капусты растут по логарифмической спирали
Слайд 38Типичный фрактал
Цветная капуста -
типичный фрактал.
Рассмотрим строение цветной капусты.
Если разрезать
один из цветков, очевидно, что в руках остаётся всё та же цветная капуста, только меньшего размера. Можно продолжать резать снова и снова, даже под микроскопом - однако все, что мы получим - это крошечные копии цветной капусты
Слайд 39Сувенир «Матрешка»
Фрактальная игрушка
Матрешка -
игрушка-сувенир - типичный фрактал.
Принцип фрактальности очевиден, когда все фигурки деревянной игрушки выстроены в ряд, а не вложены друг в друга.
Слайд 40Человек – это фрактал!
Рождается ребенок, растет, становится взрослым и этот процесс
сопровождается принципом «самоподобия», фрактальностью.
Слайд 41 «Математика представляет собой
собрание выводов, которые могут
быть применены к
чему угодно»
Бертран Рассел
Бертран Рассел
Слайд 43Фракталы в литературе
У попа была собака,
он ее любил.
Она съела кусок мяса,
он ее убил.
В землю закопал,
Надпись
написал:
У попа была собака…
У попа была собака…
Вот море,
А на море сyша,
А на сyше пальма,
А на пальме клоп сидит
И видит:
Море, а на море сyша…
Слайд 44Фракталы в литературе
«Вот дом.
Который построил Джек.
А вот пшеница.
Которая в тёмном чулане
храница
В доме,
Который построил Джек
А вот весёлая птица-синица,
Которая ловко ворует пшеницу,
Которая в тёмном чулане храница
В доме,
Который построил Джек…».
В доме,
Который построил Джек
А вот весёлая птица-синица,
Которая ловко ворует пшеницу,
Которая в тёмном чулане храница
В доме,
Который построил Джек…».
Слайд 45Фракталы в телекоммуникации
Для передачи данных на расстояния используются антенны,
имеющие фрактальные
формы,
что сильно уменьшает их размеры и вес
что сильно уменьшает их размеры и вес
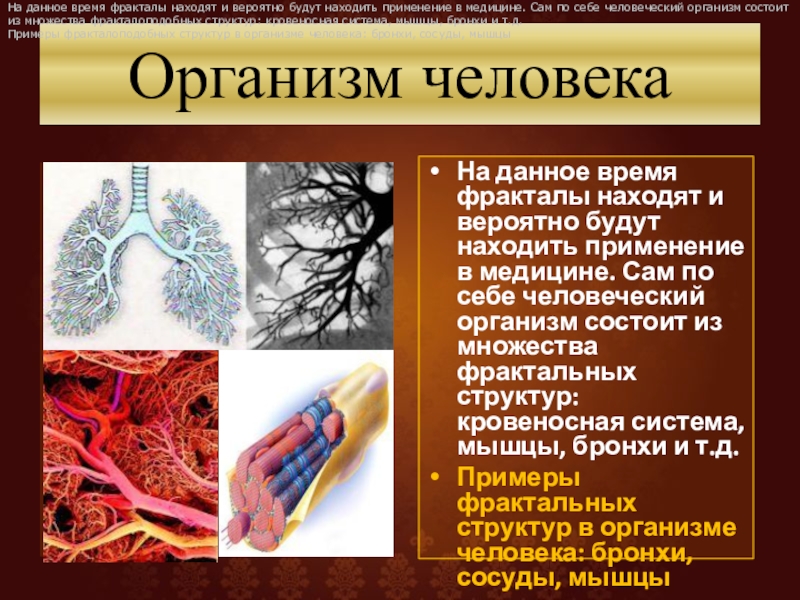
Слайд 46Организм человека
На данное время фракталы находят и вероятно будут находить применение
в медицине. Сам по себе человеческий организм состоит из множества фрактальных структур: кровеносная система, мышцы, бронхи и т.д.
Примеры фрактальных структур в организме человека: бронхи, сосуды, мышцы
Примеры фрактальных структур в организме человека: бронхи, сосуды, мышцы
На данное время фракталы находят и вероятно будут находить применение в медицине. Сам по себе человеческий организм состоит из множества фракталоподобных структур: кровеносная система, мышцы, бронхи и т.д.
Примеры фракталоподобных структур в организме человека: бронхи, сосуды, мышцы
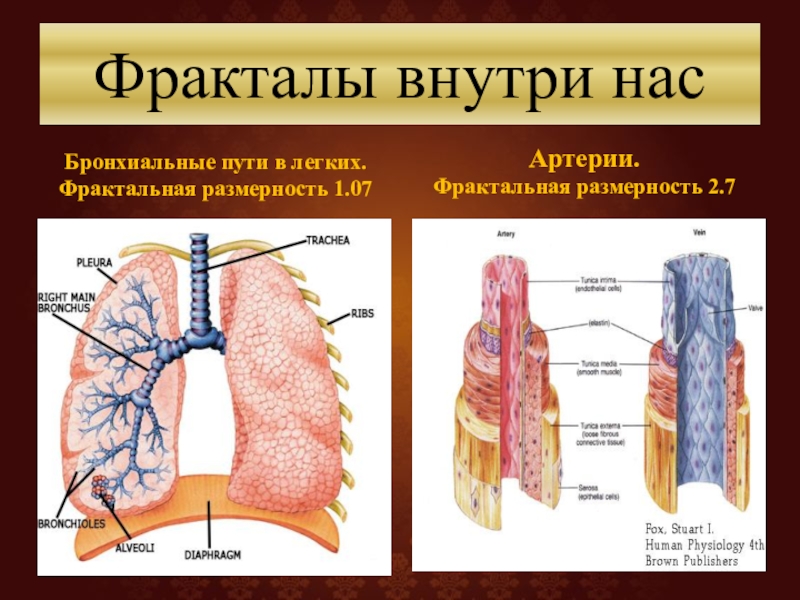
Слайд 47Фракталы внутри нас
Бронхиальные пути в легких.
Фрактальная размерность 1.07
Артерии.
Фрактальная размерность 2.7
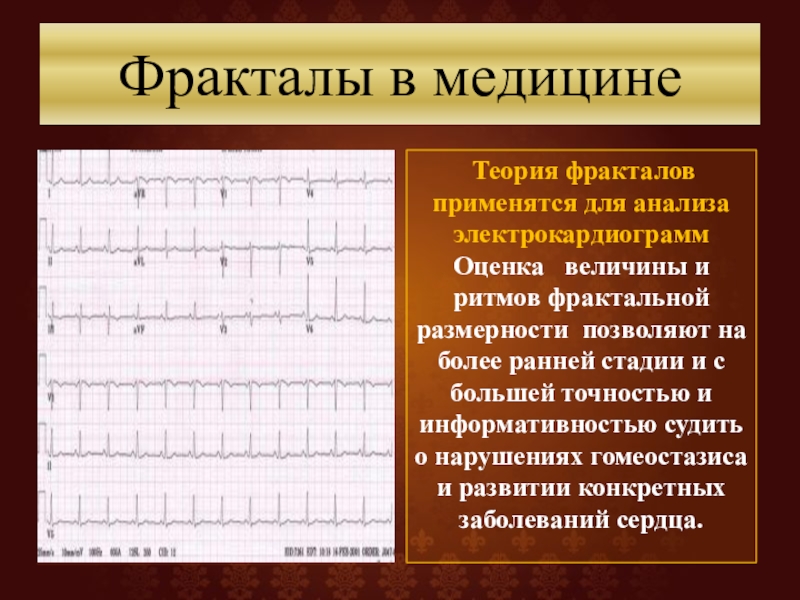
Слайд 48Фракталы в медицине
Теория фракталов применятся для анализа электрокардиограмм
Оценка
величины и ритмов фрактальной размерности позволяют на более ранней стадии и с большей точностью и информативностью судить о нарушениях гомеостазиса и развитии конкретных заболеваний сердца.
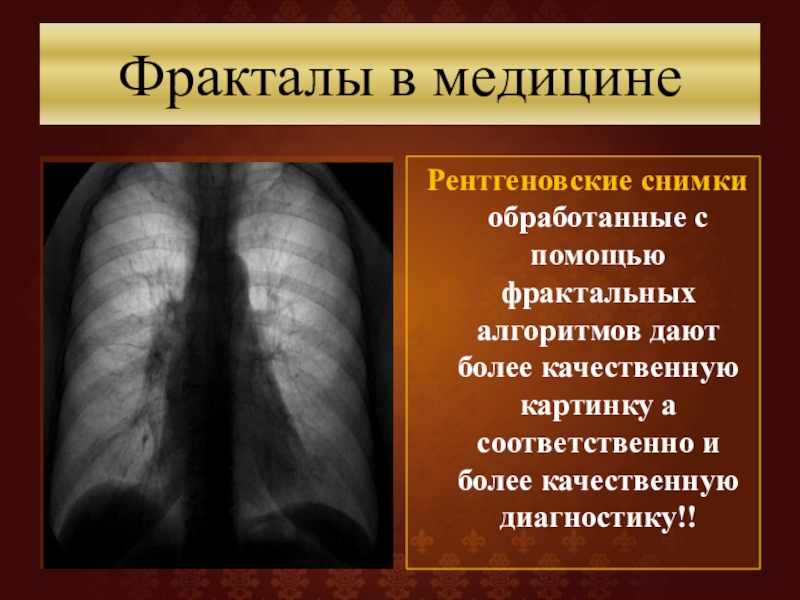
Слайд 49Фракталы в медицине
Рентгеновские снимки обработанные с помощью фрактальных алгоритмов дают
более качественную картинку а соответственно и более качественную диагностику!!
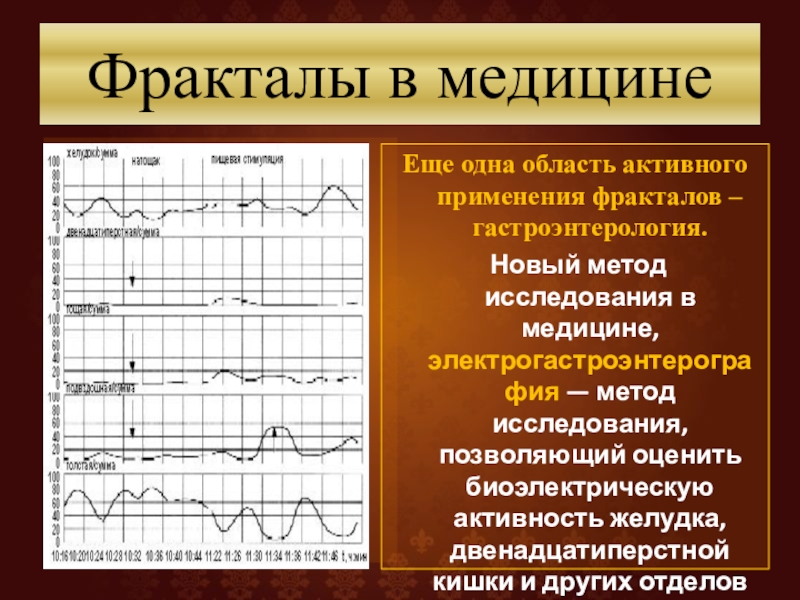
Слайд 50Фракталы в медицине
Еще одна область активного применения фракталов –гастроэнтерология.
Новый
метод исследования в медицине, электрогастроэнтерография — метод исследования, позволяющий оценить биоэлектрическую активность желудка, двенадцатиперстной кишки и других отделов ЖКТ.
Слайд 51Фракталы в архитектуре
Фрактальный принцип развития природных и геометрических объектов проникает вглубь
архитектуры и как образ внешнего решения объекта, и как внутренний принцип архитектурного формообразования
Слайд 52Фракталы в дизайне
Дизайнеры со всего мира начали использовать в своих работах
замечательные фрактальные структуры, только недавно описанные видными математиками.
Использование фракталов поставило практически все направления современного дизайна на новый уровень.
Привнесение фрактальных структур увеличило во многих случаях как визуальную, так и функциональную составляющие дизайна.
.
Использование фракталов поставило практически все направления современного дизайна на новый уровень.
Привнесение фрактальных структур увеличило во многих случаях как визуальную, так и функциональную составляющие дизайна.
.
Слайд 53Фракталы в мебели.
Дизайнер Такеси Миякава
в детстве мечтал стать математиком.
Иначе
как объяснить этот предмет мебели: тумбочка Fractal 23 содержит 23 ящика самых разных размеров и пропорций, которые как-то ухитряются уживаться между собой внутри кубического корпуса, заполняя почти всё доступное им пространство.
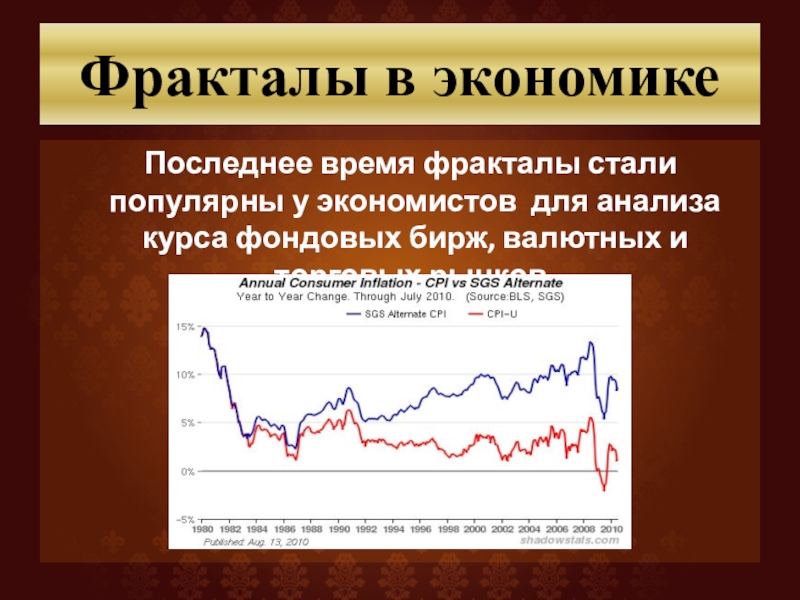
Слайд 54Фракталы в экономике
Последнее время фракталы стали популярны у экономистов
для анализа курса фондовых бирж, валютных и торговых рынков.
Слайд 55Фракталы в играх
Сегодня в очень многих играх (пожалуй
самый яркий пример Minecraft),
где присутствуют разного рода природные ландшафты, так или иначе используются фрактальные алгоритмы. Создано большое количество программ для генерации ландшафтов и пейзажей, основанных на фрактальных алгоритмах.
где присутствуют разного рода природные ландшафты, так или иначе используются фрактальные алгоритмы. Создано большое количество программ для генерации ландшафтов и пейзажей, основанных на фрактальных алгоритмах.
Слайд 56Фракталы в кино
В кино для создания различных фантастических пейзажей используется фрактальный
алгоритм. Фрактальная геометрия позволяет художникам по спецэфффектам без труда создавать такие объекты как облака, дым, пламя, звёздное небо и т.д. Что уж тогда говорить о фрактальной анимации, это действительное потрясающее зрелище.
Слайд 57Электронная музыка
Зрелищность фрактальной анимации с успехом используют и виджеи.Особенно
часто такие видеоинсталляции используются на концертах исполнителей электронной музыки.
Слайд 58Естественные науки
Очень часто фракталы применяются в геологии и геофизике. Не секрет
что побережья островов и континентов имеют некоторую фрактальную размерность, зная которую можно очень точно вычислить длины побережий.
Исследование разломной тектоники и сейсмичности порой тоже исследуется с помощью фрактальных алгоритмов.
Геофизика использует фракталы и фрактальный анализ для исследования аномалий магнитного поля, для изучения распространение волн и колебаний в упругих средах, для исследования климата и многих других вещей.
Исследование разломной тектоники и сейсмичности порой тоже исследуется с помощью фрактальных алгоритмов.
Геофизика использует фракталы и фрактальный анализ для исследования аномалий магнитного поля, для изучения распространение волн и колебаний в упругих средах, для исследования климата и многих других вещей.
Слайд 59Фракталы в физике
В физике фракталы применяются очень широко
В
физике твёрдых тел фрактальные алгоритмы позволяют точно описывать и предсказывать свойства твёрдых, пористых, губчатых тел, аэрогелей. Это помогает в создании новых материалов с необычными и полезными свойствами.
Пример твёрдого тела - кристаллы.
Пример твёрдого тела - кристаллы.
Слайд 60Изучение турбулентности
Изучение турбулентности в потоках очень хорошо подстраивается под фракталы.
Турбулентные
потоки хаотичны и поэтому их сложно точно смоделировать.
И здесь помогает переход к из фрактальному представлению, что сильно облегчает работу инженерам и физикам, позволяя им лучше понять динамику сложных систем
И здесь помогает переход к из фрактальному представлению, что сильно облегчает работу инженерам и физикам, позволяя им лучше понять динамику сложных систем
Слайд 62Фракталы в биологии
В биологии они применяются для моделирования популяций и
для описания систем внутренних органов (система кровеносных сосудов).
После создания кривой Коха было предложено использовать её
при вычислении протяжённости береговой линии.
После создания кривой Коха было предложено использовать её
при вычислении протяжённости береговой линии.
Слайд 64«Мир устроен не только причудливей,
чем мы думаем, но и
причудливей,
чем мы можем предполагать»
Джон Холдейн
чем мы можем предполагать»
Джон Холдейн
Слайд 78Наши достижения
Приняли участие с работой « Путешествие в мир фракталов» в
VII Всероссийской олимпиаде школьников и студентов «Наука 2.0» по учебному предмету «Математика». Заняли первое место.
Приняли участие с работой «Путешествие в мир фракталов» во Всероссийском конкурсе «Великие открытия и изобретения». Заняли первое место.
Приняли участие с работой «Путешествие в мир фракталов» в VIII Всероссийской олимпиаде школьников и студентов «Я – исследователь» по учебному предмету Математика. Заняли первое место.
Приняли участие с работой «Путешествие в мир фракталов» во Всероссийском конкурсе «Великие открытия и изобретения». Заняли первое место.
Приняли участие с работой «Путешествие в мир фракталов» в VIII Всероссийской олимпиаде школьников и студентов «Я – исследователь» по учебному предмету Математика. Заняли первое место.
Слайд 79Гимн фракталам!
Можно с полной уверенностью сказать об огромном практическом применении фракталов
и фрактальных алгоритмов на сегодняшний день.
Спектр областей где применяются фракталы очень обширен.
И наверняка, в ближайшем обозримом будущем, перечень областей где будут применятся фракталы будет только пополняться!!!
Спектр областей где применяются фракталы очень обширен.
И наверняка, в ближайшем обозримом будущем, перечень областей где будут применятся фракталы будет только пополняться!!!
Слайд 80Результаты работы:
Познакомились с историей возникновения и развития фрактальной геометрии;
Изучили виды фракталов,
их применение в современном мире.
Создали собственные фракталы на языках программирования Pascal и Logo
Создали научную работу о фракталах, опубликовали ее в сети Интернет.
Создали брошюры «Фракталы вокруг нас», «Применение фракталов»
Провели внеклассные мероприятия «Удивительный мир фракталов» для учащихся 8-11классов.
Создали собственные фракталы на языках программирования Pascal и Logo
Создали научную работу о фракталах, опубликовали ее в сети Интернет.
Создали брошюры «Фракталы вокруг нас», «Применение фракталов»
Провели внеклассные мероприятия «Удивительный мир фракталов» для учащихся 8-11классов.
