Анна
Проверила Шевчук Е.И.
- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад Признаки подобия треугольников
Содержание
- 1. Презентация Признаки подобия треугольников
- 2. Пропорциональные
- 3. Совершимпутешествие в страну«ПОДОБИЯ»
- 4. Определение подобных треугольников Два треугольника называются
- 5. АВСА1В1С1 ▲ АВС ~ ▲А1В1С1
- 6. Отношение площадей подобных треугольников Отношением площадей
- 7. Отношение площадей подобных треугольниковБиссектриса треугольника делит противоположную сторону на отрезки, пропорциональные прилежащим сторонам треугольника.
- 8. Отсюда перейдем
- 9. ТРЕМ ПРИЗНАКАМПОДОБИЯ ТРЕУГОЛЬНИКОВ
- 10. Первый признак подобия треугольников
- 11. Если два угла одного треугольника соответственно равны
- 12. Второйпризнак подобия треугольников
- 13. Если две стороны одного треугольника пропорциональны двум
- 14. Третийпризнак подобия треугольников
- 15. Если три стороны одного треугольника пропорциональны трём
- 16. ПУТЕШЕСТВИЕк . . .
- 17. Средней линией треугольника называется
- 18. Медианы треугольника пересекаются в
- 19. Высота прямоугольного треугольника, проведенная
- 20. Есть еще кое-что,но я в этом пока не «БУМ-БУМ»
- 21. Применение подобия
- 22. Применение подобия
- 23. Я надеюсь, что моя презентация будет вам полезна. Спасибо за внимание!
Пропорциональные отрезкиОтношением отрезков AB и CD называется отношение их длин, т.е. Отрезки AB и CD пропорциональны отрезкам A1B1 и C1D1, если
Слайд 1Презентация по геометрии на тему: «Признаки подобия треугольников»
Выполнила ученица 8 класса
Чмутова
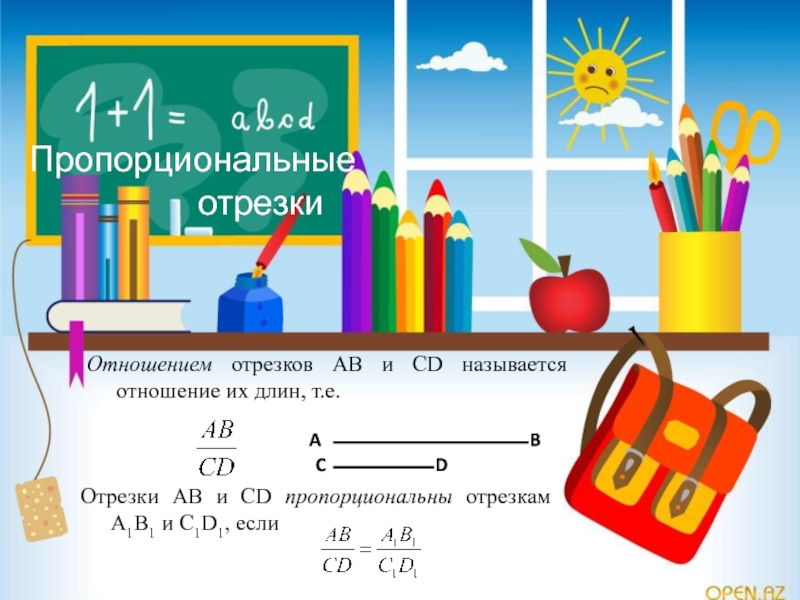
Слайд 2Пропорциональные
отрезки
Отношением
отрезков AB и CD называется отношение их длин, т.е.
Отрезки AB и CD пропорциональны отрезкам A1B1 и C1D1, если
Слайд 4Определение подобных
треугольников
Два треугольника называются подобными, если их углы
соответственно равны и стороны одного треугольника пропорциональны сходственным сторонам другого треугольника.
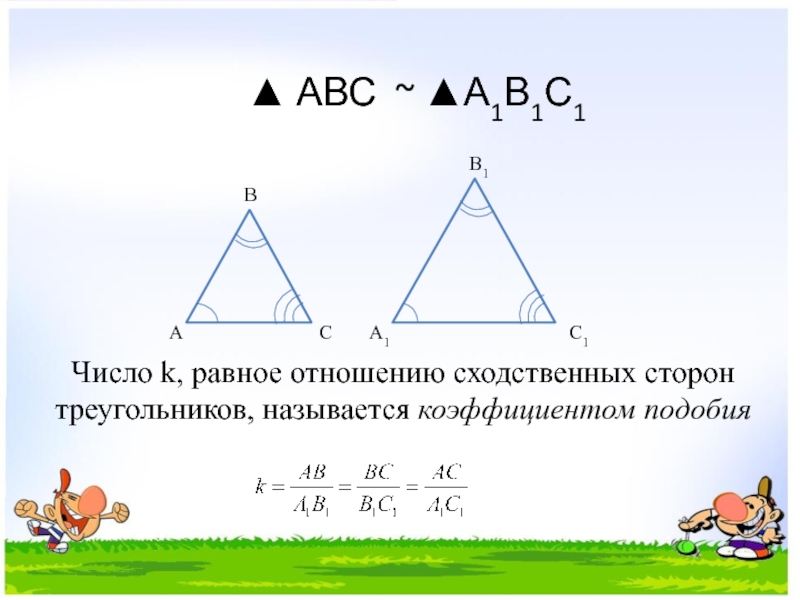
▲ АВС ~ ▲А1В1С1
Слайд 5А
В
С
А1
В1
С1
▲ АВС ~ ▲А1В1С1
Число k, равное отношению сходственных сторон треугольников, называется коэффициентом подобия
Слайд 6Отношение площадей подобных треугольников
Отношением площадей двух подобных треугольников равно
квадрату коэффициента подобия
Слайд 7Отношение площадей подобных треугольников
Биссектриса треугольника делит противоположную сторону на отрезки, пропорциональные
прилежащим сторонам треугольника.
Слайд 11Если два угла одного треугольника соответственно равны двум углам другого треугольника,
то такие треугольники подобны.
Дано:
▲АВС и ▲А1В1С1
∟А=∟А1;
∟В= ∟ В1;
Док-ть:
▲АВС ~ ▲А1В1С1
А
А1
В
В1
С
С1
Док-во:
Рассмотрим ▲АВС ~ ▲А1В1С1: у ∟А=∟А1
у ∟В= ∟ В1 => ▲АВС ~ ▲А1В1С1
( по I пр. п. тр.) – ч.т.д.
Слайд 13Если две стороны одного треугольника пропорциональны двум сторонам другого треугольника и
углы, заключённые между этими сторонами, равны, то такие треугольники подобны.
А
А1
В
В1
С1
С
Дано:
▲АВС и ▲А1В1С1
∟А=∟А1;
АВ:А1В1=АС:А1С1;
Док - ть:
▲АВС~▲А1В1С1
Док – во:
Рассмотрим ▲АВС и ▲А1В1С1: у ∟А=∟А1;
с АВ:А1В1;
С АС:А1С1;=>▲АВС~▲А1В1С1(по II пр. п. тр.)
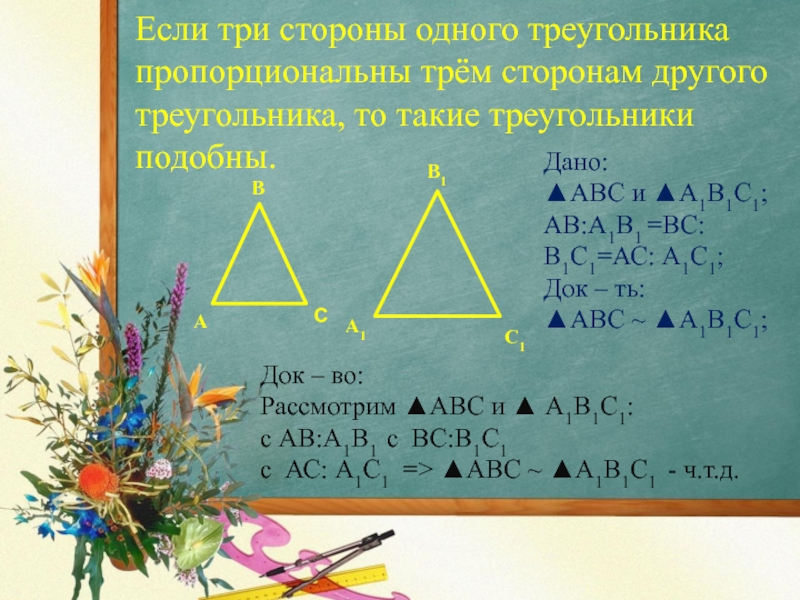
Слайд 15Если три стороны одного треугольника пропорциональны трём сторонам другого треугольника, то
такие треугольники подобны.
А
А1
В
В1
С1
С
Дано:
▲АВС и ▲А1В1С1;
АВ:А1В1 =ВС:В1С1=АС: А1С1;
Док – ть:
▲АВС ~ ▲А1В1С1;
Док – во:
Рассмотрим ▲АВС и ▲ А1В1С1:
с АВ:А1В1 с ВС:В1С1
с АС: А1С1 => ▲АВС ~ ▲А1В1С1 - ч.т.д.
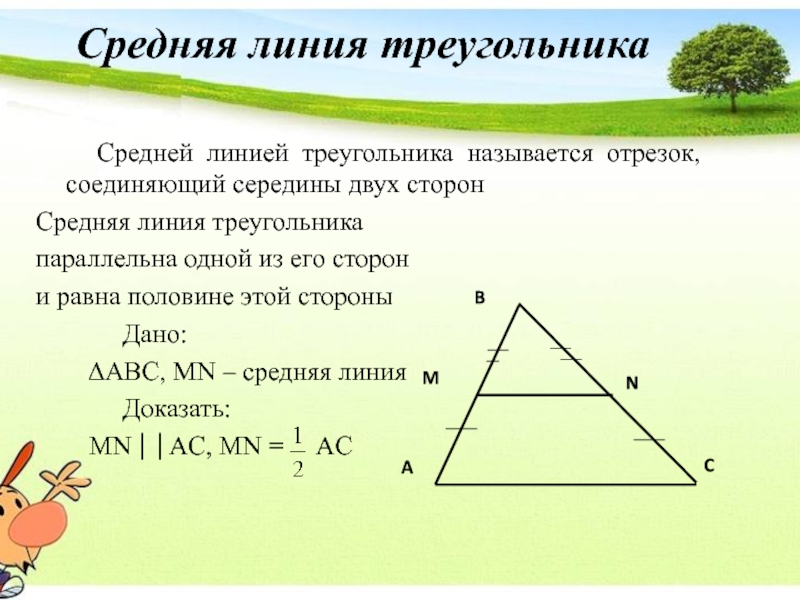
Слайд 17 Средней линией треугольника называется отрезок, соединяющий середины двух
сторон
Средняя линия треугольника
параллельна одной из его сторон
и равна половине этой стороны
Дано:
ABC, MN – средняя линия
Доказать:
MNAC, MN = AC
Средняя линия треугольника
параллельна одной из его сторон
и равна половине этой стороны
Дано:
ABC, MN – средняя линия
Доказать:
MNAC, MN = AC
Средняя линия треугольника
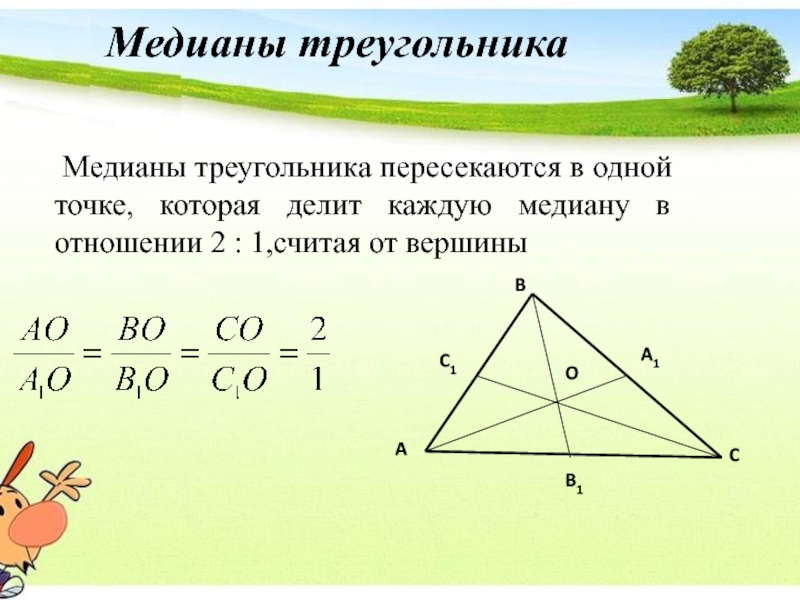
Слайд 18 Медианы треугольника пересекаются в одной точке, которая делит
каждую медиану в отношении 2 : 1,считая от вершины
Медианы треугольника
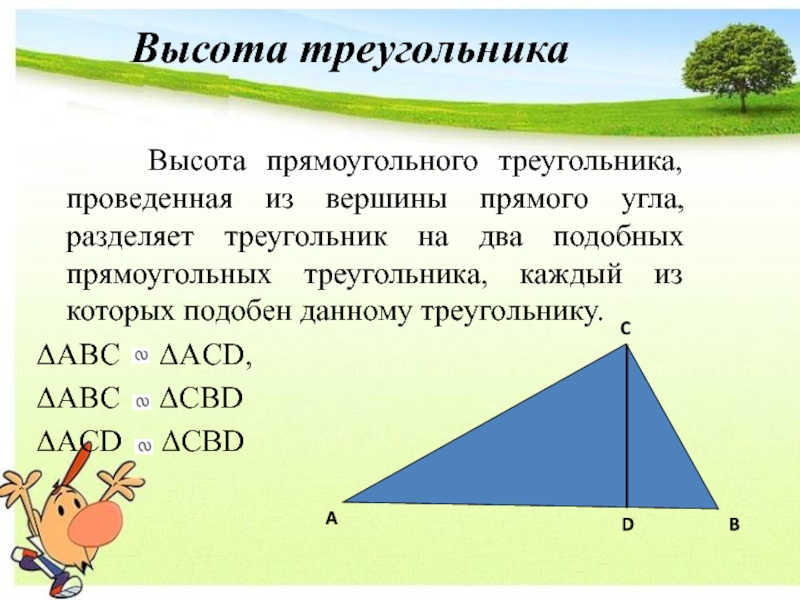
Слайд 19 Высота прямоугольного треугольника, проведенная из вершины прямого угла,
разделяет треугольник на два подобных прямоугольных треугольника, каждый из которых подобен данному треугольнику.
ABC ACD,
ABC CBD
ACD CBD
ABC ACD,
ABC CBD
ACD CBD
Высота треугольника
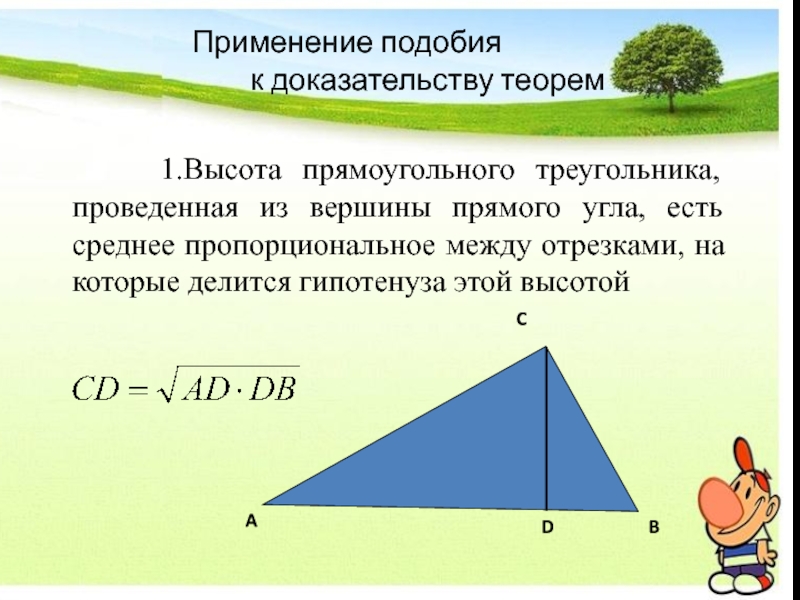
Слайд 21Применение подобия
к доказательству теорем
1.Высота прямоугольного треугольника, проведенная из вершины прямого угла, есть среднее пропорциональное между отрезками, на которые делится гипотенуза этой высотой
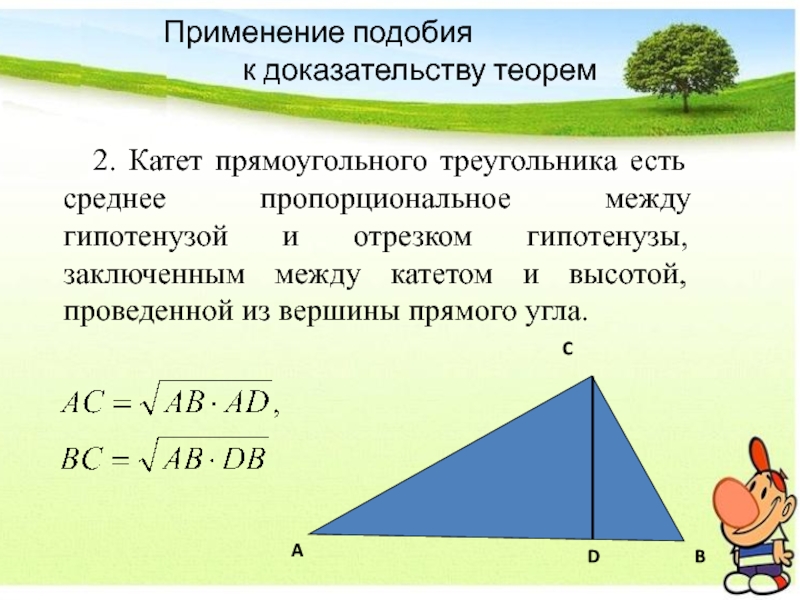
Слайд 22Применение подобия
к доказательству теорем
2. Катет прямоугольного треугольника есть среднее пропорциональное между гипотенузой и отрезком гипотенузы, заключенным между катетом и высотой, проведенной из вершины прямого угла.
