- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад Применение теоремы Пифагора
Содержание
- 1. Презентация Применение теоремы Пифагора
- 2. Актуальность данного исследования. существует около 500 различных
- 3. Цель работы: выявить кто открыл теорему Пифагора,
- 4. Великий древнегреческий ученый Пифагор родился на острове
- 5. Литература Пифагор и его теорема воспеты в
- 6. О теореме ПифагораУделом истины не может быть
- 7. Не в силах преградить той истине дорогу,Они,
- 8. Любовный треугольник ПифагораЗдесь не помогут ямб и
- 9. постичь без всякой геометрии:лбом - об углы!
- 10. Использование теоремы Пифагора в архитектуре и строительствеВ
- 11. Вычислить площадь двускатной крышиРешение:1. Из Δ АВС
- 12. В физикеМолниеотвод , громоотвод , устройство для
- 13. Легенда о смерти Пифагора Сонную
- 14. Если дан нам треугольник И притом с
- 15. Заключение. Теорема Пифагора позволяет находить длину отрезка
Слайд 1
Применение
теоремы
Пифагора
Выполнили: А.Горелкин, Е. Бондарева МБОУ Полужская ООШ
Слайд 2Актуальность данного исследования.
существует около 500 различных доказательств этой теорем (геометрических,
Объект исследования: теорема Пифагора.
Предмет исследования: применение теоремы Пифагора в различных областях
Слайд 3Цель работы:
выявить кто открыл теорему Пифагора, рассмотреть её применение в
Задачи:
1.Познакомиться с биографией Пифагора и деятельностью пифагорейского союза.
2.Показать применение теоремы Пифагора в литературе
Слайд 4Великий древнегреческий ученый Пифагор родился на острове Самос в VI веке
Пифагор Самосский
Слайд 5Литература Пифагор и его теорема воспеты в литературе. Существуют много легенд, мифов, рассказов,
Пребудет вечной истина, как скоро
Ее познает слабый человек!
И ныне теорема Пифагора
Верна, как и в его далекий век.
Обильно было жертвоприношенье
Богам от Пифагора. Сто быков
Он отдал на закланье и сожженье
За света луч, пришедший с облаков.
Поэтому всегда с тех самых пор,
Чуть истина рождается на свет,
Быки ревут, ее почуя, вслед.
Они не в силах свету помешать.
А могут лишь, закрыв глаза, дрожать
От страха, что вселил в них Пифагор
Слайд 6О теореме Пифагора
Уделом истины не может быть забвенье,
Как только мир ее
И теорема та, что дал нам Пифагор,
Верна теперь, как в день ее рожденья.
За светлый луч с небес вознес благодаренье
Мудрец богам не так, как было до тех пор.
Ведь целых сто быков послал он под топор,
Чтоб их сожгли как жертвоприношенье.
Быки с тех пор, как только весть услышат,
Что новой истины уже следы видны,
Отчаянно мычат и ужаса полны:
Им Пифагор навек внушил тревогу.
Слайд 7Не в силах преградить той истине дорогу,
Они, закрыв глаза, дрожат и
Суть истины вся в том, что нам она-навечно,
Когда хоть раз в прозрений ее увидим свет,
И теорема Пифагора через столько лет
Для нас, как для него, бесспорна, безупречна.
На радостях богам был Пифагором дан обет:
За то, что мудрости коснулся бесконечной,
Он сто быков заклал, благодаря предвечных;
Моленья и хвалы вознес он жертве вслед.
С тех пор быки, когда, учуют, тужась,
Что к новой истине людей опять подводит след,
Ревут остервенело, так что слушать мочи нет,
Такой в них Пифагор вселил навеки ужас,
Быкам, бессильным новой правде противостоять,
Что остается? - Лишь, глаза закрыв, реветь, дрожать.
Слайд 8Любовный треугольник Пифагора
Здесь не помогут ямб и дольник,
хорей и дактиль грудь
Попав в любовный треугольник,
готовься выдюжить и выстоять,
на плечи взять хрустальным грузом
сознанье: разобьешься вдребезги! -
И по его гипотенузе
пройти, страховкою побрезговав;
измерить все своим аршином,
и торопясь - ведь все мы смертные! -
его углы, его вершины
Слайд 9постичь без всякой геометрии:
лбом - об углы! Вершины - приступом
сердечным, нитроглицериновым
(уж если кудри серебристые,
не дорожить же сердцевиною!)
Ни теореме Пифагора
не поддается он, ни времени -
Любви Бермудский Треугольник
разносторонний, тазобедренный
Слайд 10Использование теоремы Пифагора в архитектуре и строительстве
В зданиях готического и романского
Примером является простое окно в готическом стиле . Способ построения его прост.
Чтобы найти площадь поверхности
двухскатной крыши, все скаты , которые имеют равный уклон , нужно умножить площадь чердака на длину стропила и разделить на половину ширины дома. Например: при строительстве любого сооружения рассчитывают расстояние , центры тяжести , размещения опор , балок и т.д.
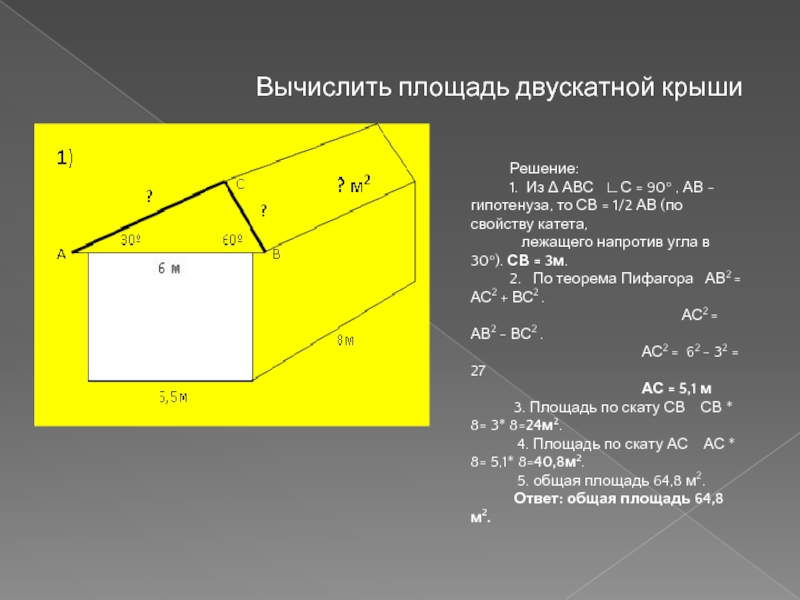
Слайд 11Вычислить площадь двускатной крыши
Решение:
1. Из Δ АВС ∟С = 90º
лежащего напротив угла в 30º). СВ = 3м.
2. По теорема Пифагора АВ2 = АС2 + ВС2 .
АС2 = АВ2 - ВС2 .
АС2 = 62 - 32 = 27
АС = 5,1 м
3. Площадь по скату СВ СВ * 8= 3* 8=24м2.
4. Площадь по скату АС АС * 8= 5,1* 8=40,8м2.
5. общая площадь 64,8 м2.
Ответ: общая площадь 64,8 м2.
Слайд 12В физике
Молниеотвод , громоотвод , устройство для защиты зданий , промышленных,
В АСТРОНОМИИ
Обитателям Марса было решено в конце 19 века послать сигнал в виде теоремы Пифагора.
Неизвестно, как это сделать; но для всех очевидно , что математический факт , выражаемый теоремой Пифагора, имеет место всюду и поэтому похожие на нас обитатели другого мира должны понять такой сигнал.
Слайд 13Легенда о смерти Пифагора
Сонную тишину ночного Метапонта прорезал
- Кто это? - спросил начальник караула у мальчика
- Это Пифагор, - ответил тот.
- Кто такой Пифагор? Среди жителей города нет гражданина с таким именем.
- Мы недавно прибыли из Кротона. Мой господин должен был скрываться от врагов, и выходил только ночью. Они выследили его и убили.
- Сколько их было?- Я этого не успел заметить в темноте. Они отбросили меня в сторону и накинулись на него. Начальник караула стал на колени и приложил руки к груди старца.
- Конец, - сказал начальник.
Слайд 14Если дан нам треугольник
И притом с прямым углом ,
То квадрат
Мы всегда легко найдём:
Катеты в квадрат возводим,
Сумму степеней находим –
И таким лёгким путём
К результату мы придем!