- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад Применение компьютера на уроке
Содержание
- 1. Презентация Применение компьютера на уроке
- 2. ЦЕЛЬ РАБОТЫ:выделить некоторые методические приёмы применения мультимедийных пособий на уроке математики в условиях перехода к ФГОС
- 3. Теоретический материалТермин «медиа» происходит от английского слова
- 4. Методика использования мультимеда технологий предполагает:Совершенствование системы управления
- 5. НАИБОЛЕЕ ЭФФЕКТИВНЫЕ ПРИЁМЫ ПРИМЕНЕНИЯ ПРЕЗЕНТАЦИЙ:При изучении нового
- 6. Три основных способа использования мультимедийных средствИллюстративный. Удачно
- 7. 1. Домашнее задание
- 8. Мультимедийные презентации уроков в среде Microsoft Power
- 9. Квадратные уравнения
- 10. Квадратные уравненияКвадратным уравнением называют уравнение вида
- 11. Пример квадратного уравнения
- 12. Следующая работа
- 13. ВекторыМБОУ СОШ № 2
- 14. Понятие вектораМногие физические величины, например сила, перемещение
- 15. Равенство векторовВекторы, лежащие либо на одной прямой,
- 16. Откладывание вектора от данной точкиОт любой точки
- 17. Начало вектораКонец вектораПонятие вектора
- 18. Равенство векторов
- 19. Следующая работаПо алгебре и началам анализа.
- 20. Презентация по Алгебре и Началам АнализаНа тему: «Функция y=cos x»»Просмотр«
- 21. Функция y=cos x, её свойства и график
- 22. yx0П-П1y=cos x
- 23. Свойства функции y=cos x1. D (f)= (-
- 24. Периодичность функции y=cos x Определение.Функцию y=f(x), x
- 25. Любое число вида 2Пk, где k=±1, ±2,
- 26. Найти основной период функции y=cos 0,5 xР
- 27. Как построить график функции y=mf(x), если известен
- 28. y0П-П11,5XП2-1,5
- 29. П2-2П-3П3П2П-П 2y0П-П11,5X-1,5
- 30. Как построить график функции y=f(kx), если известен
- 31. Зная график функции y=f(x), построить график функции
- 32. y0X-142-237y=f(2x)y=f(x)
- 33. Построить график функции y=cos 2xРешение: Построим полуволну
- 34. Зная график функции y=f(x) построить график функции
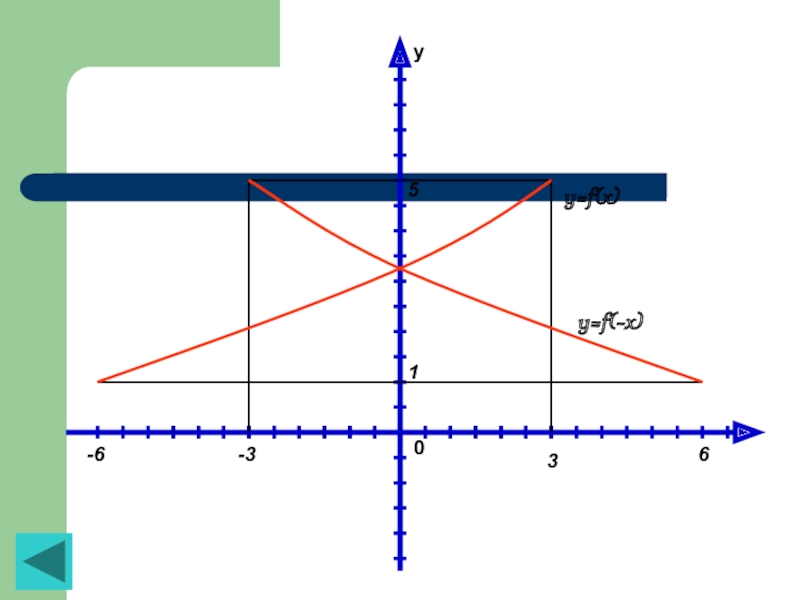
- 35. y01563-3-6y=f(x)y=f(-x)
- 36. Зная график функции y=f(x), построить график функции y=f(kx), где k – отрицательное число.При k
- 37. Построить график функции y=-3cos(-2x).Р е ш е
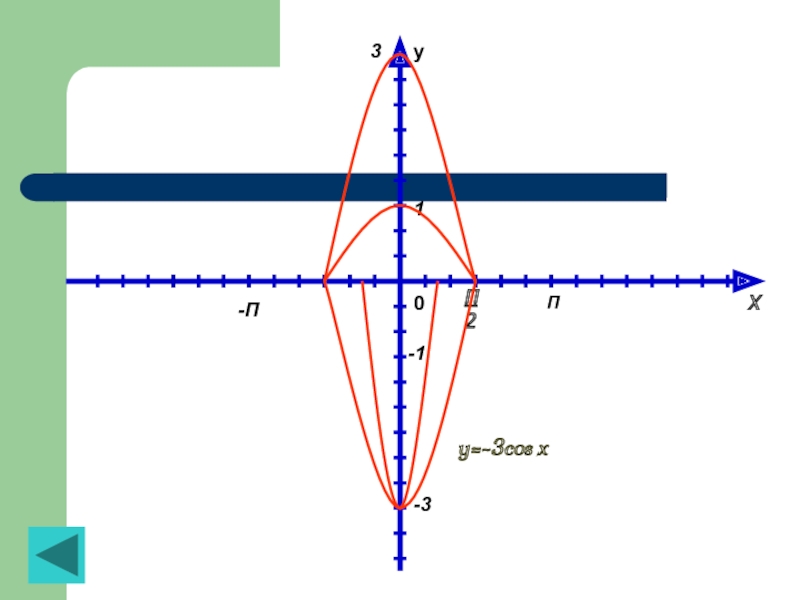
- 38. y0П-П1XП23-1-3y=-3cos x
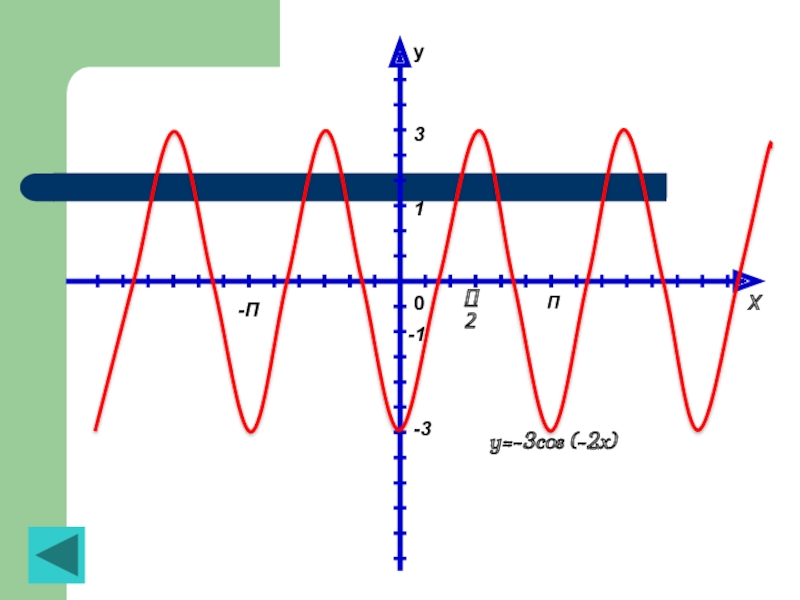
- 39. y0П-П1XП23-1-3y=-3cos (-2x)
- 40. Векторы
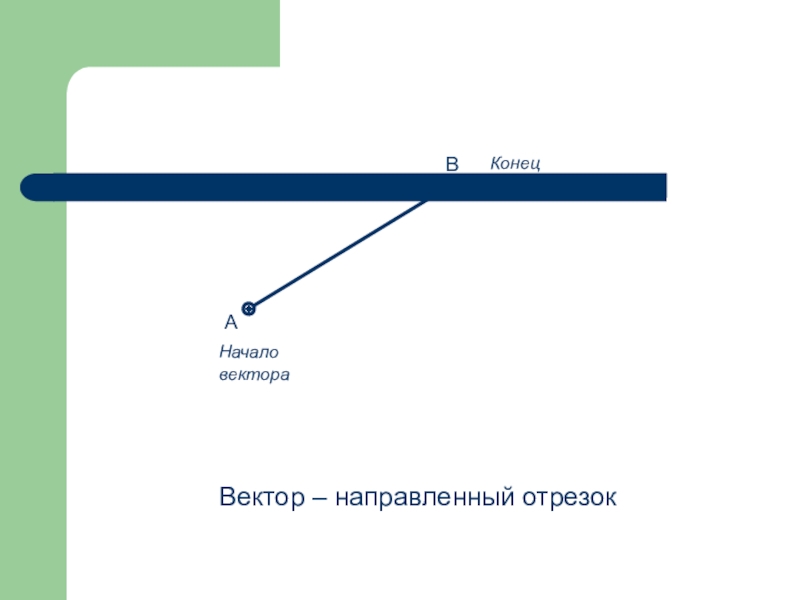
- 41. Вектор – направленный отрезок
- 42. Нулевой вектор -любая точка плоскости
- 43. Слайд 43
- 44. Коллинеарные векторы-Ненулевые векторы, лежащие на одной прямой, либо на параллельных прямыхНулевой вектор считается коллинеарным любому вектору
- 45. Слайд 45
- 46. Сонаправленные векторы-Коллинеарные векторы, имеющие одинаковое направление
- 47. Слайд 47
- 48. Противоположно направленные векторы-Коллинеарные векторы, имеющие противоположное направление
- 49. Слайд 49
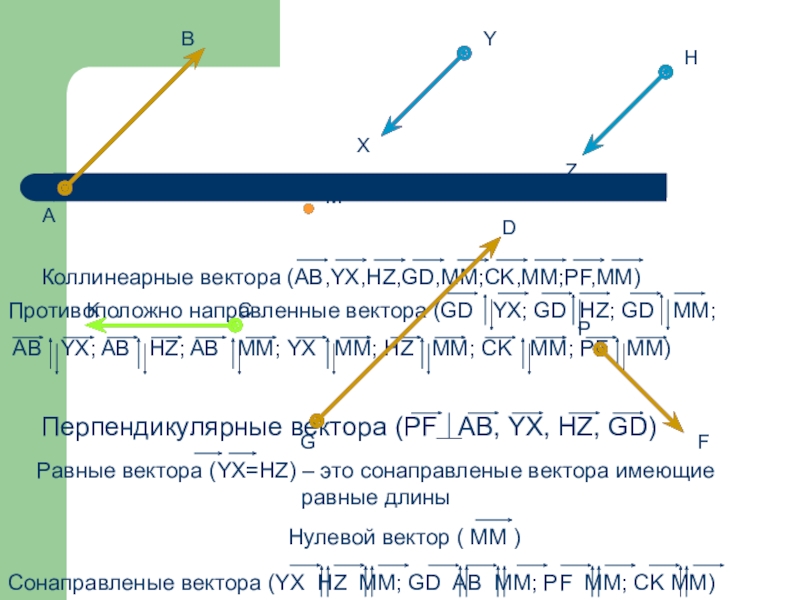
- 50. Равные векторы -равные по длине и имеющие одно направление
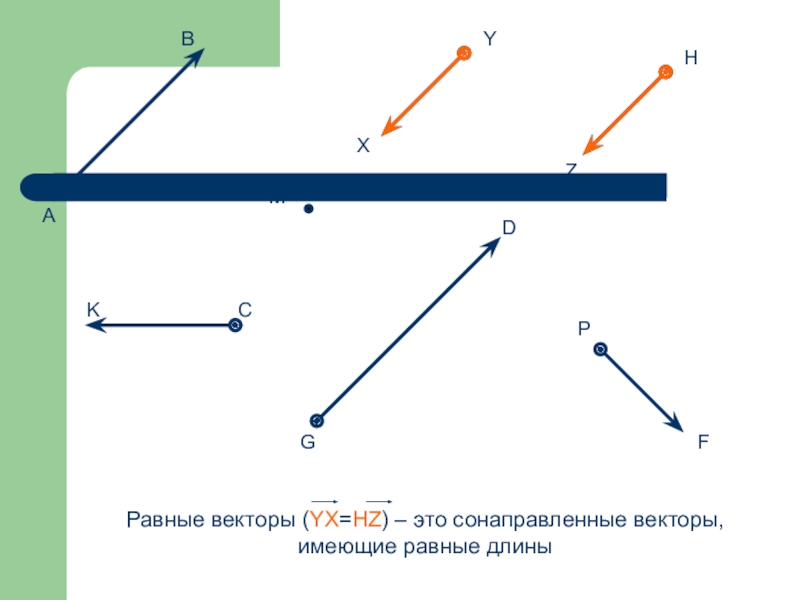
- 51. Равные векторы (YX=HZ) – это сонаправленные векторы, имеющие равные длиныМ
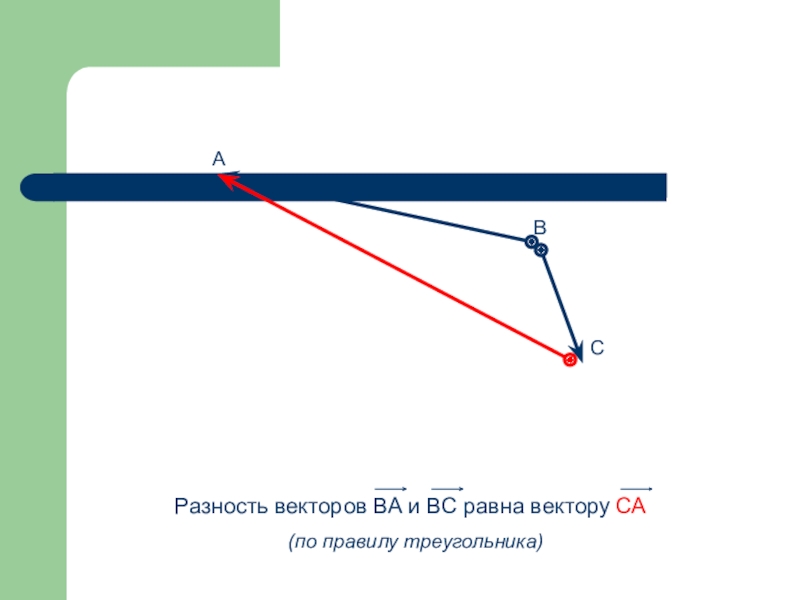
- 52. Разность векторов -Векторы вычитаются по правилу треугольника и многоугольника
- 53. Правило треугольника
- 54. Слайд 54
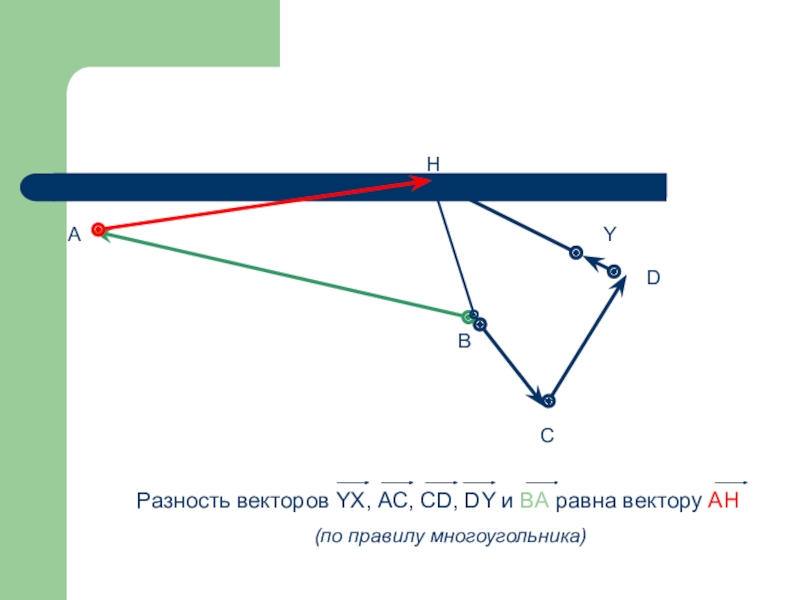
- 55. Правило многоугольника -
- 56. ABCDYH
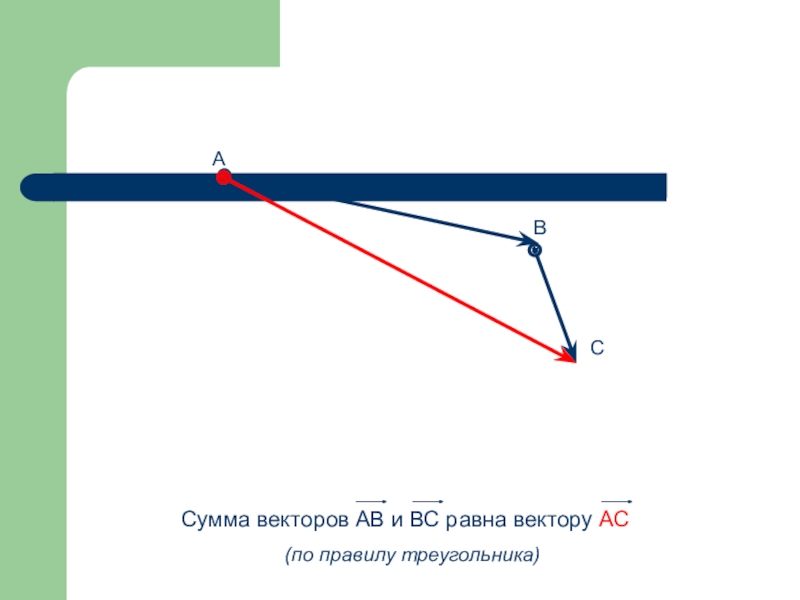
- 57. Сумма векторов -Векторы складываются по правилу треугольника, параллелограмма и многоугольника
- 58. Правило треугольника
- 59. ABC
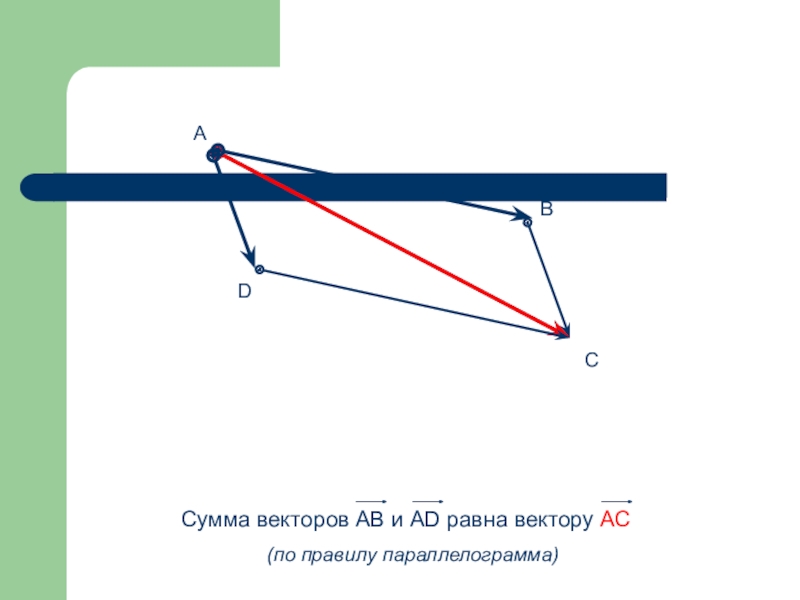
- 60. Правило параллелограмма
- 61. C
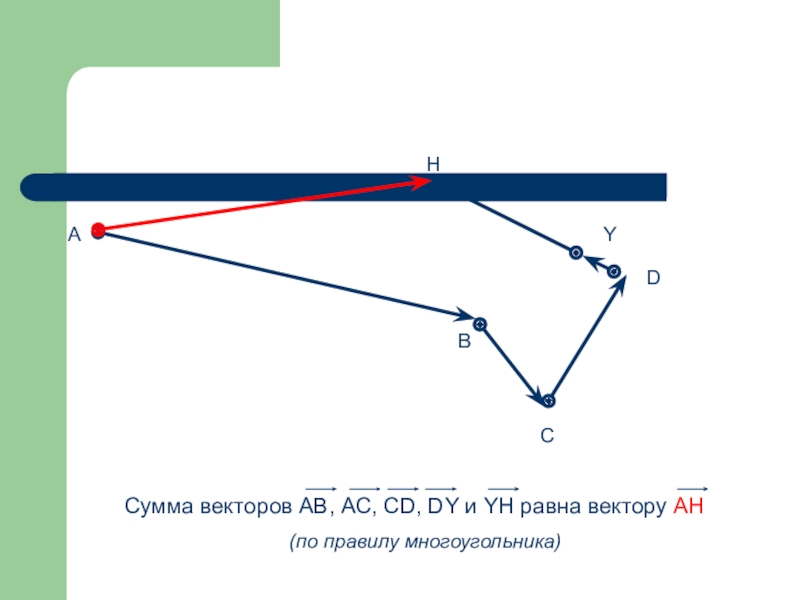
- 62. Правило многоугольника -
- 63. ABCDYH
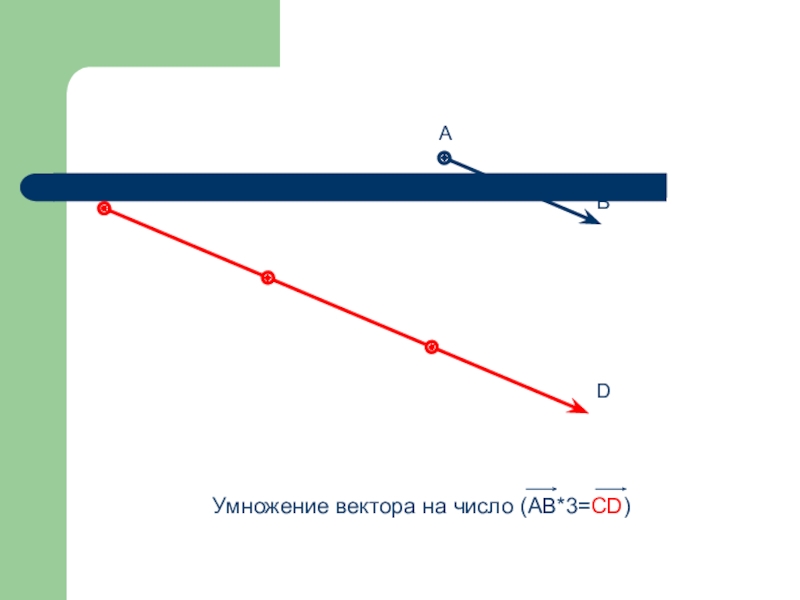
- 64. Умножение вектора на число
- 65. Слайд 65
- 66. Слайд 66
- 67. Формулы приведения.Тригонометрия. Формулы, применяемые при решении уравнений
- 68. Формулы приведения. Примеры.
- 69. Слайд 69
- 70. Способ выведения формул приведений: 1. если под
- 71. Примеры. Некоторые формулы, применяемые при решении уравнений
- 72. Слайд 72
- 73. ТЕСТКакие из данных
- 74. Радианная мера двух углов треугольника равна П/3
- 75. Какие из условий могут выполняться одновременно: 1)
- 76. Какая из данных функций четная? а) у
- 77. Решить уравнение: 2sin x – 1
- 78. Вычислить : sin 105º ответ: а) б) в) г)
- 79. Упростить: sin(a + ß) – sina· cosß
- 80. Вычислить: Sin74ºcos16º + cos74ºsin16º ответ: а)1; б) 0; в) ¼; г) –1.
- 81. Вычислить: arctg(-1) + arctg 0 ответ: а)3п/4 б) 0; в)П; г)П/2
- 82. Ответы: 1а,2б,3в,4в,5б,6а,7б,8а,9а
- 83. Основные выводы преимущества мт недостатки мт
- 84. заключениеВопрос: «Вводить или нет мультимедиа в образовательные
- 85. Спасибо за внимание
Слайд 1Создание и использование мультимедийных материалов на уроке математики
Исполнители: Т.А. Юстус, учитель
Слайд 2ЦЕЛЬ РАБОТЫ:
выделить некоторые методические приёмы применения мультимедийных пособий на уроке математики
Слайд 3Теоретический материал
Термин «медиа» происходит от английского слова media – «средства массовой
«Мультимедиа» - совокупность программно-аппаратных средств, отображающих
информацию в зрительном и звуковом виде
Слайд 4Методика использования мультимеда технологий предполагает:
Совершенствование системы управления обучением на различных этапах
Усиление мотивации учения
Повышение информационной культуры и знаний по предмету
Улучшение качества обучения
Повышение уровня подготовки уч-ся в области современных информационных технологий
Демонстрацию возможностей компьютера, не только как средство для игры
Слайд 5НАИБОЛЕЕ ЭФФЕКТИВНЫЕ
ПРИЁМЫ ПРИМЕНЕНИЯ ПРЕЗЕНТАЦИЙ:
При изучении нового материала
При проведении устных упражнений
При проверке
При проверке письменных работ (самостоятельных, домашних и др.)
Слайд 6Три основных способа использования мультимедийных средств
Иллюстративный. Удачно подобранный визуальный ряд иллюстрирует
. Схематичный. Конструирование опорных конспектов или логических схем.
Интерактивный. Сочетает в себе элементы иллюстративного и схематичного подходов.
Слайд 8Мультимедийные презентации уроков в среде Microsoft Power Point
Динамические элементы на слайдах:
Способствуют лучшему пониманию и запоминанию материала
Даёт возможность добиваться активизации познавательной активности
Повышается эмоциональная насыщенность урока
Задействованы все каналы восприятия уч-ся (зрительный, слуховой, эмоциональный, механический)
Слайд 10Квадратные уравнения
Квадратным уравнением называют уравнение вида
где коэффициенты а, b, c – любые действительные числа, причем а ≠0
а – первый, или старший коэффициент;
b – второй коэффициент;
с – свободный член.
Слайд 11Пример квадратного уравнения
Решить квадратное уравнение:
a=3, b=8, c=11,
D=b²-4ac=8²-4×3×(-11)=64+132=196
Ответ: 1;
Слайд 14Понятие вектора
Многие физические величины, например сила, перемещение материальной точки, скорость, характеризуются
Отрезок, для которого указано, какая из его граничных точек считается началом, а какая – концом, называется направленным отрезком или вектором.
Определение
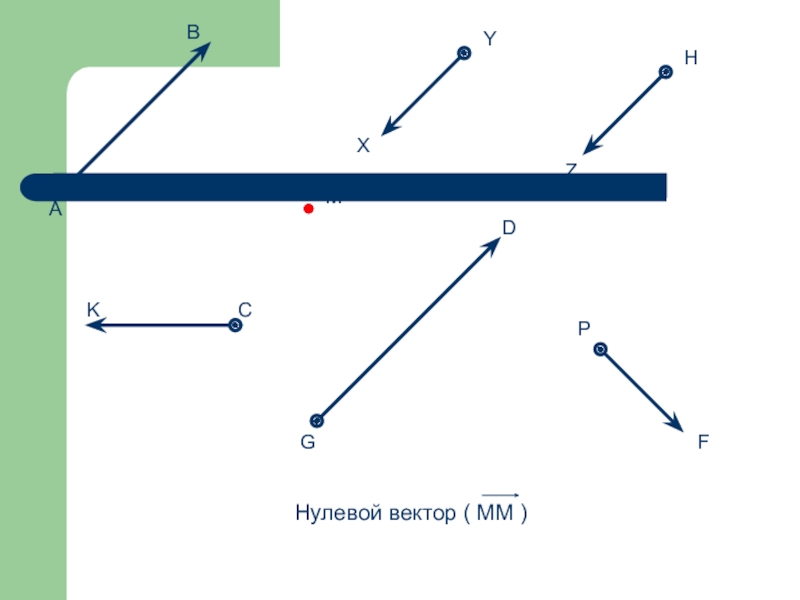
На рисунках вектор изображается отрезком со стрелкой, показывающей направление вектора. Векторы обозначают либо одной строчной латинской буквой со стрелкой над ней, либо двумя заглавными латинскими буквами со стрелкой над ними, например . Любая точка плоскости также является вектором. В этом случае вектор называется нулевым. Начало нулевого вектора совпадает с его концом, на рисунке такой вектор изображается одной точкой. Если, например, точка, изображающая нулевой вектор, обозначена точкой M, то данный нулевой вектор можно обозначить так:
Длиной или модулем ненулевого вектора называется длина отрезка AB. Длина нулевого вектора считается равной нулю.
Содержание
Просмотр
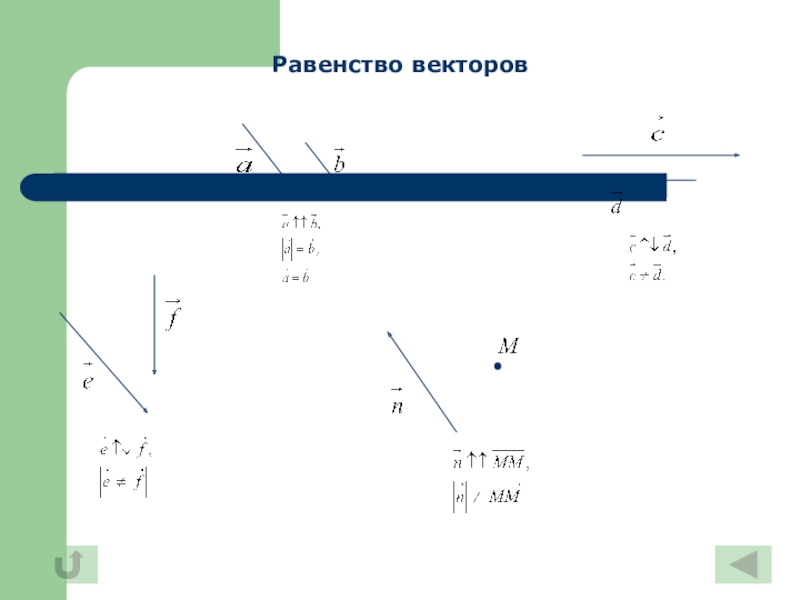
Слайд 15Равенство векторов
Векторы, лежащие либо на одной прямой, либо на параллельных прямых
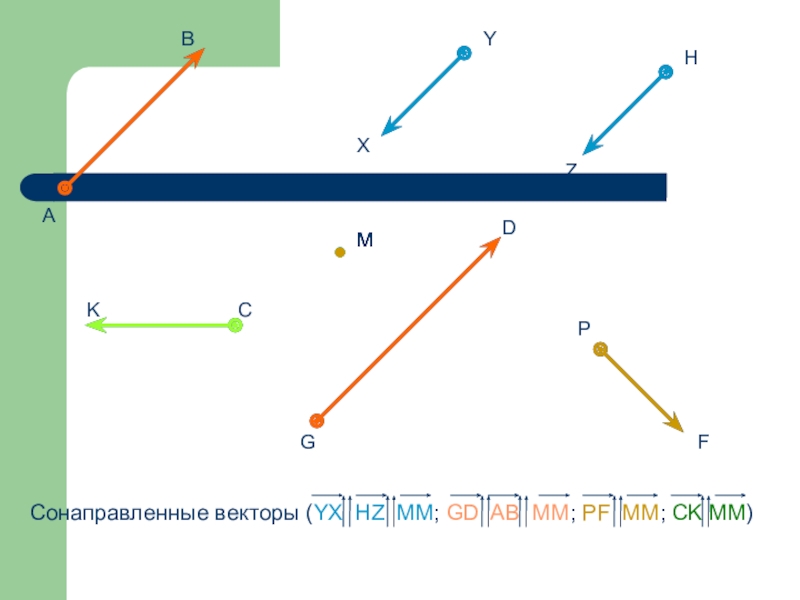
Если два ненулевых вектора и коллинеарны, то они могут быть направлены либо одинаково, либо противоположно. В первом случае векторы называются сонаправленными, а во втором – противоположно направленными. Сонаправленность векторов обозначается следующим образом: Если же векторы и противоположно направлены, то это обозначают так: . Нулевой вектор сонаправлен с любым вектором.
Определение
Векторы называются равными, если они сонаправлены и их длины равны.
Просмотр
Содержание
Слайд 16Откладывание вектора от данной точки
От любой точки M можно отложить вектор,
Замечание
Равные векторы, отложенные от разных точек, часто обозначают одной и той же буквой. Иногда про такие векторы говорят, что это один и тот же вектор, но отложенный от разных точек.
Содержание
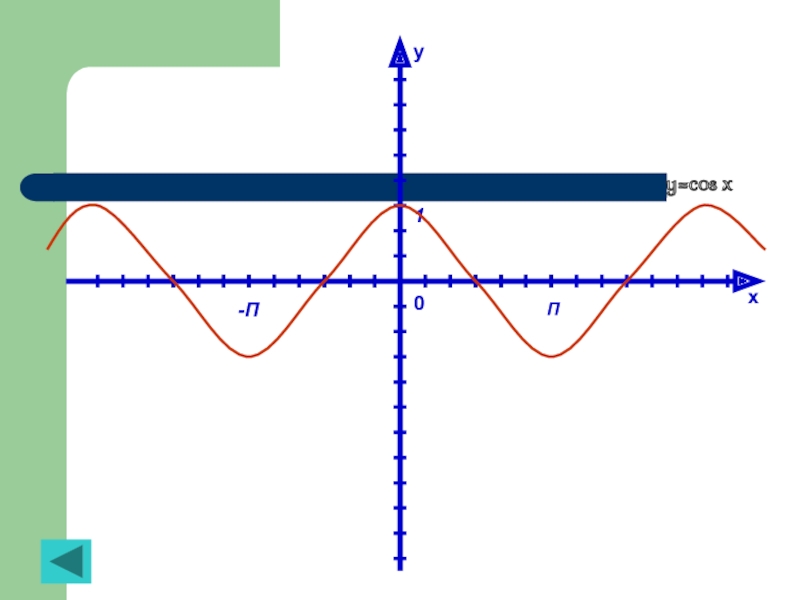
Слайд 21Функция y=cos x, её свойства и график
График функции График функции
Свойства функции Свойства функции y=cos x
Периодичность функции Периодичность функции y=cos x
Построение графика функции Построение графика функции y=mf(x)Построение графика функции y=mf(x),Построение графика функции y=mf(x), Построение графика функции y=mf(x), где Построение графика функции y=mf(x), где f=cos x
Построение графика функции Построение графика функции y=f(kx)Построение графика функции y=f(kx),Построение графика функции y=f(kx), Построение графика функции y=f(kx), где Построение графика функции y=f(kx), где f=cos x
Слайд 23Свойства функции y=cos x
1. D (f)= (- ∞;+ ∞)
2. y=cos x
3. Функция убывает на отрезке [0; П], возрастает на отрезке [П; 2П] и т. д.
4. Функция ограничена сверху и снизу
5. yнаим. = -1(этого значения функция достигает в любой точке вида x = П+2Пk); yнаиб. = 1 (этого значения функция достигает в любой точке вида x = 2Пk)
6. E (f)= [-1; 1]
7. Период функции y=cos x равен 2Пk
Слайд 24Периодичность функции y=cos x
Определение.
Функцию y=f(x), x є X, называют периодической,
f(x-T)=f(x)=f(x+T)
Число T, удовлетворяющее указанному условию, называют периодом функции y=f(x).
Отсюда следует, что, поскольку для любого x справедливo равенствo
cos(x-2П) = cos x = cos(x+2П),
функция y=cos x является периодической и число 2П служит периодом для этой функции.
Вывод:
Если функция y=f(x) имеет период T, то для построения графика функции нужно сначала построить ветвь(волну, часть) графика на любом промежутке длины T(чаще всего берут промежуток с концами в точках 0 иT или – T/2 и T/2), а затем сдвинуть эту ветвь по оси x вправо и влево на T, 2T, 3T и т.д.
Слайд 25Любое число вида 2Пk, где k=±1, ±2, ±3, … ,является периодом
Пример
Основной период функции y=cos kx равен 2П/k
Слайд 26Найти основной период функции y=cos 0,5 x
Р е ш е н
Пусть T – основной период функции y=cos 0,5x. Положим f(x)=cos 0,5x. Тогда
f(x+T)= cos 0,5(x+T)=cos (0,5x+0,5T)
Чтобы число T было периодом функции, должно выполняться тождество cos(0,5x+0,5T) = cos0,5x.
Значит, 0,5T = 2Пn. Но, поскольку речь идет об отыскании основного периода, получаем 0,5T = 2П, T = 4П
Ответ: T = 4П
Слайд 27Как построить график функции y=mf(x), если известен график функции y=f(x), где
Пример: Построить график функции y=-1,5cos x
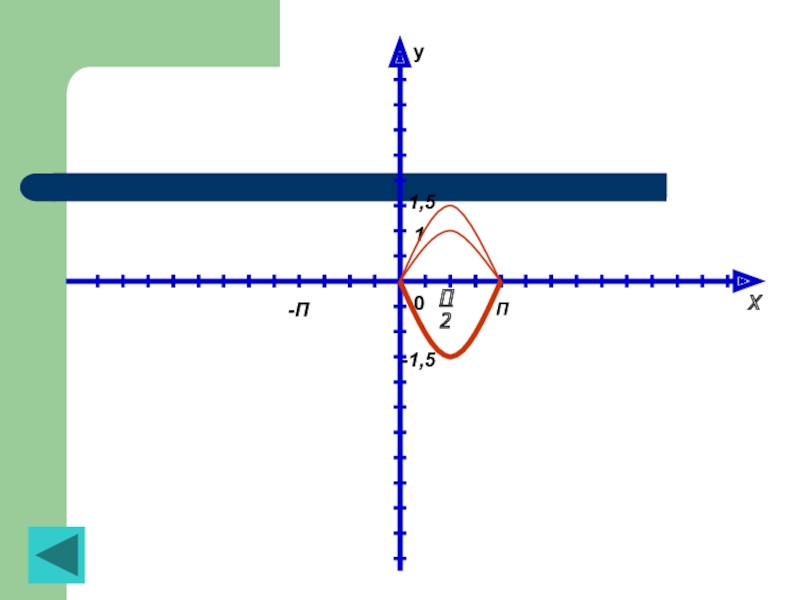
Решение: 1) Построим график функции y=cos x, точнее, одну полуволну графика(пунктирная линия на рисунке 1).
2) Осуществим растяжение построенного графика от оси x с коофицентом 1,5; получим одну полуволну графика функции y=1,5cos x (тонкая линия на рис. 1)
3) Подвергнем построенную полуволну графика функции y=1,5cos x преобразованию симметрии относительно оси x; получим полуволну графика функции y=-1,5cos x (она выделена на рис. 1)
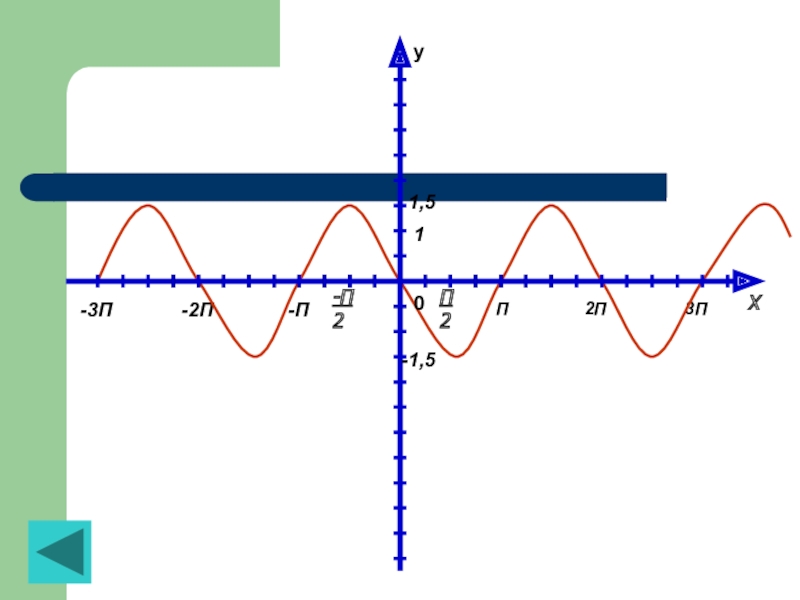
4) С помощью построенной полуволны получаем весь график функции y=-1,5cos x (рис. 2)
Рисунок 1
Рисунок 2
Слайд 30Как построить график функции y=f(kx), если известен график функции y=f(x), где
Рассмотрим несколько случаев.
Задача №1
Задача №2
Задача №3
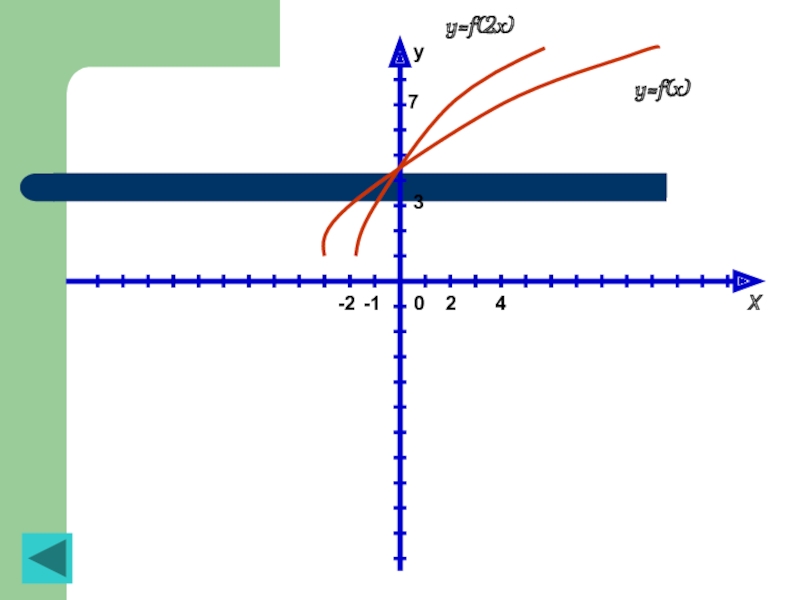
Слайд 31Зная график функции y=f(x), построить график функции y=f(kx), где k –
Пусть на графике функции y=f(x) имеются точки (4; 7) и (-2; 3). Это значит, что f(4)=7 и f(-2)=3. Если x=2, то y = f(2x) = f(2*2) = f(4) = 7. Значит, на графике функции y= f(2x) есть точка (2; 7). Далее, если x= -1, то y = f(2x) = f(-1*2) = f(-2) = 3. Значит, на графике функции y=f(2x) есть точка (-1; 3). Итак, на графике y=f(x) есть точки (4; 7) а на графике y=f(2x) есть точки (2; 7) и (-1; 3), т. е. точки с той же ординатой, но с абсциссой в два раза меньшей (по модулю). Так же обстоит дело и с другими точками графика функции y-f(x), когда мы переходим к графику функции y-f(x) (рис. 1). Такое преобразование называют сжатием к оси ординат с коофицентом 2.
Рисунок 3
Пример
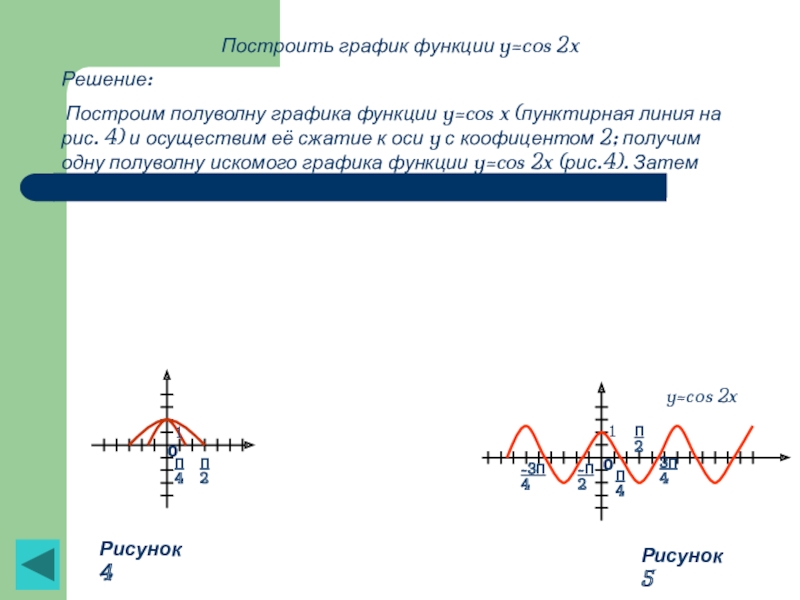
Слайд 33Построить график функции y=cos 2x
Решение:
Построим полуволну графика функции y=cos
Рисунок 4
Рисунок 5
y=cos 2x
0
1
П4
П2
3П 4
-П 2
П4
П2
1
0
-3П 4
Слайд 34Зная график функции y=f(x) построить график функции y=f(kx), где k=-1.
Итак, точке (3; 5), принадлежащей графику функции y=f(x), соответствует точка (-3; 5), принадлежащей графику функции y=f(-x); точке (-6; 1), принадлежащей графику функции y=f(x), соответствует точка (6; 1), принадлежащей графику функции y=f(-x). Указанные пары точек симметричны относительно оси y (рис. 6)
Обобщая эти рассуждения, приходим к следующему выводу: график функции y=f(-x) можно получить из графика функции y=f(x) с помощью преобразования симметрии относительно оси y.
З а м е ч а н и е. Если речь идет о построении графика функции y=f(-x), то обычно проверяют, является ли функция y=f(x) четной или нечетной. Если y=f(x) - четная функция, то график функции y=f(-x) совпадает с графиком функции y=f(x). Если y=f(x) – нечетная функция, то вместо графика функции y=f(-x) можно построить график функции y=-f(x) .
Рисунок 6
Слайд 36Зная график функции y=f(x), построить график функции y=f(kx), где k –
При k<0 справедливо равенство f(kx) = f(-|k|x). Значит, речь идет о построении графика функции y=f(-|k|x). Это можно сделать в три шага:
Построить график функции y=f(x);
Осуществить его сжатие (или растяжение) к оси y с коофицентом |k|;
Сжатый (или растянутый) график подвергнуть преобразованию симметрии относительно оси y.
Пример
Слайд 37Построить график функции y=-3cos(-2x).
Р е ш е н и е:
Заметим прежде
Построим график функции y=cos x, точнее, одну полуволну графика (рис. 7. Все предварительные построения обозначены пунктирными линиями)
Осуществим растяжение построенного графика от оси x с коофицентом 3; получим одну полуволну графика функции y=3cosx.
Подвергнем построенную полуволну графика функции y=3cosx преобразованию симметрии относительно оси x; получим полуволну графика функции y=-3cosx.
Осуществим для полуволны графика функции y=-3cosx сжатие к оси y с коофицентом 2; получим полуволну графика функции y=-3cos2x (рисю7, сплошная линия).
С помощью полученной полуволны построим весь график (рис. 8)
Рисунок 7
Рисунок 8
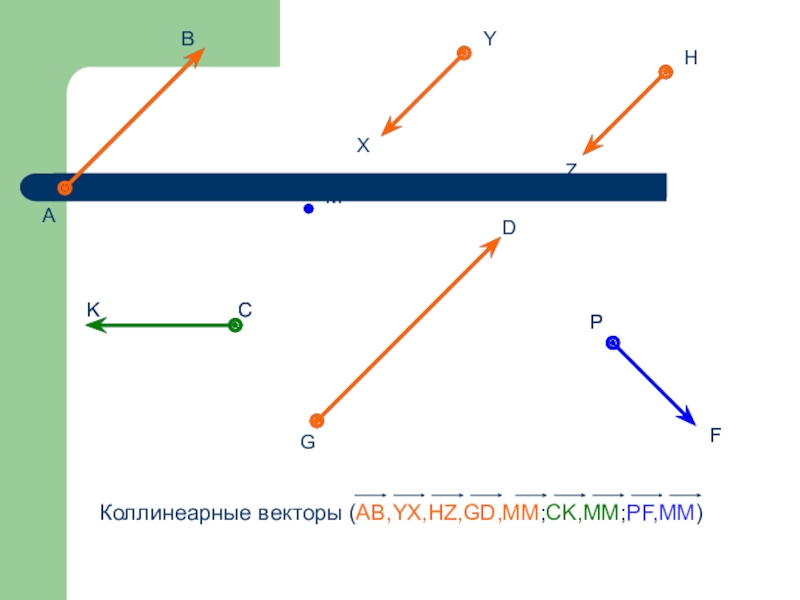
Слайд 44Коллинеарные векторы-
Ненулевые векторы, лежащие на одной прямой, либо на параллельных прямых
Нулевой
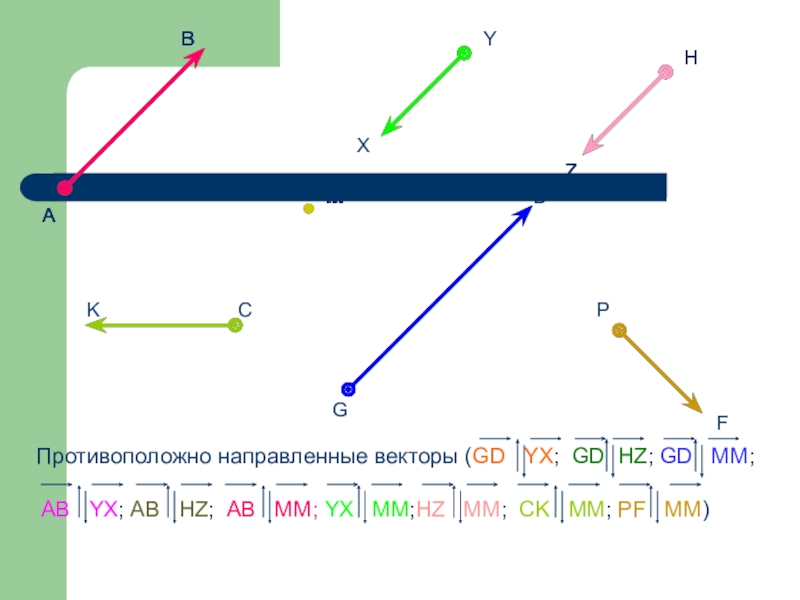
Слайд 48Противоположно направленные векторы-
Коллинеарные векторы, имеющие противоположное направление
Слайд 57Сумма векторов -
Векторы складываются по правилу треугольника, параллелограмма и многоугольника
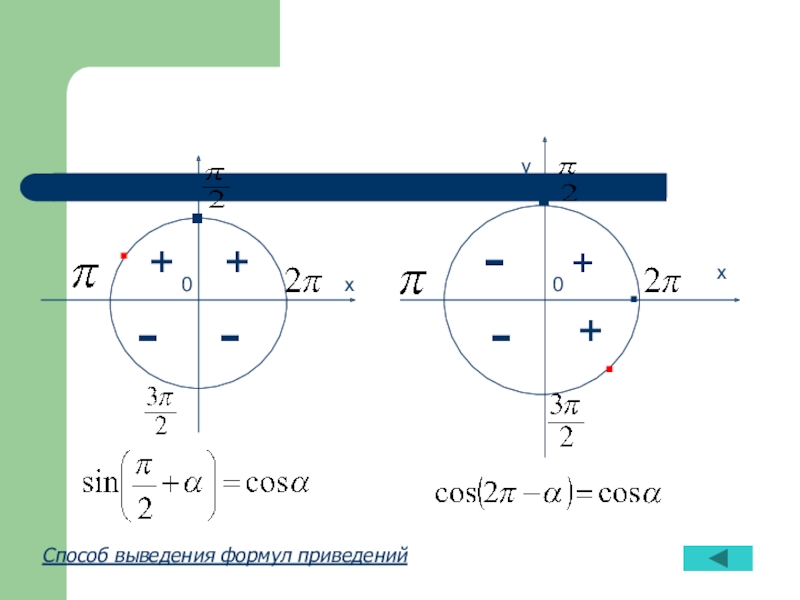
Слайд 70Способ выведения формул приведений:
1. если под знаком преобразуемой тригонометрической функции
2. если под знаком преобразуемой тригонометрической функции содержится сумма аргументов вида , то наименование тригонометрической функции изменяется.
3. перед полученной функцией от аргумента t надо поставить тот знак, который имела бы преобразуемая функция при условии, что 0
Слайд 73 ТЕСТ
Какие из данных уравнений не имеют решения
Cos x = П/3;
sin x = 3/П;
3) tg x = 3/П;
4) ctg x = П/3
Ответ: а) 1; б) 1и2; в) 3и4; г) 4
Слайд 74Радианная мера двух углов треугольника равна П/3 и П/4. Найдите градусную
Слайд 75Какие из условий могут выполняться одновременно: 1) sin a = 1, cos
Слайд 76Какая из данных функций четная? а) у = tg x + sin
Слайд 77Решить уравнение: 2sin x – 1 = 0 Ответы: а)(-1)narcsin½+пn б)(-1)nП/6+ пn, n€ z в)другой
Слайд 83Основные выводы преимущества мт недостатки мт
Интерес к материалу
заинтересованность в Получении более высокого результата
Темп и объём излагаемого материала индивидуальный
Повышен уровень использования наглядности
Повышение производительности урока
Материал при подачи выстраивается логически
(ученик продумывает слайд за слайдом)
Рассеивание внимания
Отсутствие выборочной «обратной связи»
Компьютер не заменяет очного преподавания, а только расширяет возможности
Обратная связь ограничивается «правильно-неправильно»
Сложность создания материалов по затратам времени