- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по теме Задача о брахистохроне
Содержание
- 1. Презентация по теме Задача о брахистохроне
- 2. Задача о брахистохроне была поставлена Иоганном Бернулли в Acta
- 3. Задача была следующей:Даны две точки А и В, лежащие в
- 4. Иоганн Бернулли не был первым, кто рассматривал
- 5. Он вычислил время, необходимое для точки, чтобы
- 6. Вернемся к Иоганну Бернулли. Он изложил задачу
- 7. Королевское общество опубликовано решение Ньютона анонимно в
- 8. Майский выпуск 1697 г. Acta Eruditorum содержал
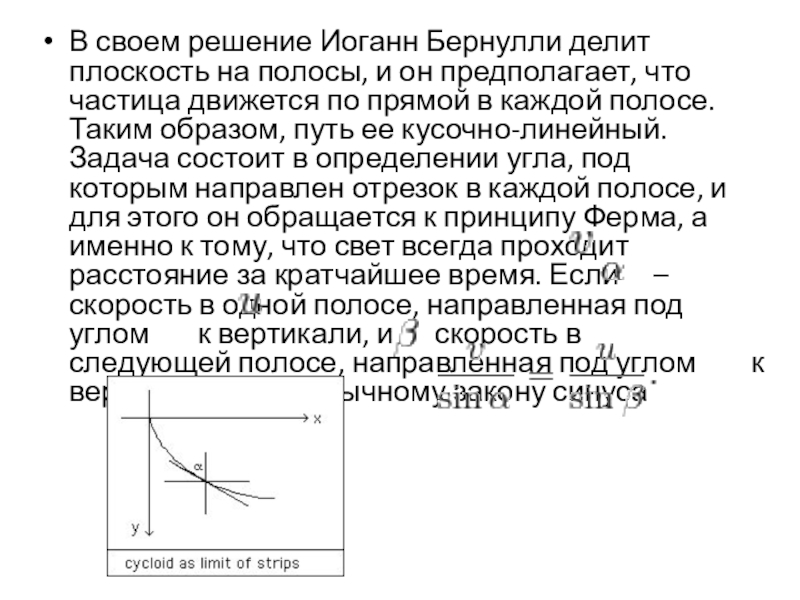
- 9. В своем решение Иоганн Бернулли делит плоскость
- 10. В пределе, когда полосы становятся бесконечно узкими,
- 11. Подстановка дает уравнение кривой
- 12. Циклоида удовлетворяет этому уравнению. Чтобы убедиться в этом, отметим, что
- 13. Гюйгенс в 1659 году показал (к этому
- 14. Иоганн Бернулли закончил свое решение задачи о
- 15. Методы, которые братья разработали для решения задач
- 16. Идея состоит в нахождении функции, на которой
- 17. Лагранж в 1760 году опубликовал эссе о
Задача о брахистохроне была поставлена Иоганном Бернулли в Acta Eruditorum в июне 1696 года. Он представил проблему следующим образом:“Я, Иоганн Бернулли, обращаюсь к самым блестящим математикам в мире. Ничто не является более привлекательным для умных людей, чем честная,
Слайд 2Задача о брахистохроне была поставлена Иоганном Бернулли в Acta Eruditorum в июне 1696
года. Он представил проблему следующим образом:
“Я, Иоганн Бернулли, обращаюсь к самым блестящим математикам в мире. Ничто не является более привлекательным для умных людей, чем честная, сложная задача, решение которой, возможно, дарует славу и останется вечным памятником. Следуя примеру Паскаля, Ферма и т.д., я надеюсь получить благодарность всего научного сообщества, указывая лучшим математикам нашего времени проблему, на которой они смогут проверить свои методы и силу своего интеллекта. Если кто-то представит мне решение предлагаемой задачи, я публично объявлю его достойным похвалы’’.
“Я, Иоганн Бернулли, обращаюсь к самым блестящим математикам в мире. Ничто не является более привлекательным для умных людей, чем честная, сложная задача, решение которой, возможно, дарует славу и останется вечным памятником. Следуя примеру Паскаля, Ферма и т.д., я надеюсь получить благодарность всего научного сообщества, указывая лучшим математикам нашего времени проблему, на которой они смогут проверить свои методы и силу своего интеллекта. Если кто-то представит мне решение предлагаемой задачи, я публично объявлю его достойным похвалы’’.
Слайд 3Задача была следующей:
Даны две точки А и В, лежащие в вертикальной плоскости. Какова траектория
точки, движущейся только под действием силы тяжести, которая начинает двигаться из А и достигает В за кратчайшее время?
Слайд 4Иоганн Бернулли не был первым, кто рассматривал задачу о брахистохроне. Галилей
в 1638 году изучал эту проблему в своей знаменитой работе “Беседы о двух новых науках’’. Его вариант задачи был сначала таким: найти прямую линию, соединяющую точку А с точкой В на вертикальной прямой, которую можно достичь за наименьшее время. Он правильно рассчитал, что такая прямая из точки А будет составлять угол в 45 градусов к вертикали при достижении необходимой вертикальной прямой в точке .
Слайд 5Он вычислил время, необходимое для точки, чтобы перейти от А к В по прямой линии,
затем он показал, что точка достигнет быстрее, если она будет двигаться по двум отрезкам АС и СВ, где С– точка на окружности.
Хотя Галилей был совершенно прав в этом, но он сделал ошибку, когда он далее утверждал, что путь наискорейшего спуска от А до В будет дугой окружности – неверное заключение.
Хотя Галилей был совершенно прав в этом, но он сделал ошибку, когда он далее утверждал, что путь наискорейшего спуска от А до В будет дугой окружности – неверное заключение.
Слайд 6Вернемся к Иоганну Бернулли. Он изложил задачу в Acta Eruditorum и
хотя и знал сам, как ее решать, бросил вызов другим. Лейбниц убедил Иоганна Бернулли дать больше времени для решения задачи, чем шесть месяцев, которые тот изначально предполагал отвести на это, чтобы зарубежные математики также имели возможность принять участие в ее решении. Было получено пять решений: Ньютона, Якоба Бернулли, Лейбница и Лопиталя плюс решение самого Иоганна Бернулли.
Слайд 7Королевское общество опубликовано решение Ньютона анонимно в Трудах Королевского общества в
январе 1697 г. Его решение было объяснено Монтегю следующим образом:
“Задача. Требуется найти кривую АDB , по которой вес, под действием своей тяжести наиболее быстро спустится из точки A в точку B .
Решение. Пусть из данной точки проведена неограниченная прямая линия APCZ параллельно горизонтали. Пусть на ней будет описана произвольная циклоида AQP , пересекающая прямую AB (предполагается, что нарисованную и представленную при необходимости) в точке Q , и вторая циклоида ADC, основание и высота которой относятся к основанию и высоте первой как AB к AQ соответственно. Последняя циклоида будет проходить через точку B, и она будет той кривой, по которой вес силой своей тяжести спустится наиболее быстро из точки A в точку B’’.
“Задача. Требуется найти кривую АDB , по которой вес, под действием своей тяжести наиболее быстро спустится из точки A в точку B .
Решение. Пусть из данной точки проведена неограниченная прямая линия APCZ параллельно горизонтали. Пусть на ней будет описана произвольная циклоида AQP , пересекающая прямую AB (предполагается, что нарисованную и представленную при необходимости) в точке Q , и вторая циклоида ADC, основание и высота которой относятся к основанию и высоте первой как AB к AQ соответственно. Последняя циклоида будет проходить через точку B, и она будет той кривой, по которой вес силой своей тяжести спустится наиболее быстро из точки A в точку B’’.
Слайд 8Майский выпуск 1697 г. Acta Eruditorum содержал решение Лейбница задачи о
брахистохроне на стр. 205, решение Иоганна Бернулли – на страницах 206-211, решение Якова Бернулли – на страницах 211-214, и латинский перевод решения Ньютона на стр. 223. Решение Лопиталя не было опубликовано до 1988 года, когда, почти 300 лет спустя, Жан Пейффер опубликовал его в Приложении 1 в P. Costabel and J. Peiffer
Слайд 9В своем решение Иоганн Бернулли делит плоскость на полосы, и он
предполагает, что частица движется по прямой в каждой полосе. Таким образом, путь ее кусочно-линейный. Задача состоит в определении угла, под которым направлен отрезок в каждой полосе, и для этого он обращается к принципу Ферма, а именно к тому, что свет всегда проходит расстояние за кратчайшее время. Если – скорость в одной полосе, направленная под углом к вертикали, и скорость в следующей полосе, направленная под углом к вертикали, то по обычному закону синуса
Слайд 10В пределе, когда полосы становятся бесконечно узкими, отрезки становятся кривой, у
которой в каждой точке угол отрезка с вертикалью становится углом касательной к кривой, который она составляет с вертикалью. Если – скорость в точке и – угол, который составляет касательная с вертикалью, то кривая удовлетворяет уравнению
Галилей показал, что скорость удовлетворяет условию
(где g– ускорение силы тяжести).
Галилей показал, что скорость удовлетворяет условию
(где g– ускорение силы тяжести).
Слайд 11Подстановка дает уравнение кривой
или
Воспользуемся тем, что и , чтобы получить
для константы
Воспользуемся тем, что и , чтобы получить
для константы
.
Слайд 13Гюйгенс в 1659 году показал (к этому его привела задача Паскаля
о циклоиде), что циклоида является решением задачи о таутохроне, а именно задачи о нахождении кривой, для которой время, затраченное частицей, скользящей вниз по ней под действием однородной силы тяжести, в самой нижней точке не зависит от выбора начальной точки.
Слайд 14Иоганн Бернулли закончил свое решение задачи о брахистохроне такими словами:
“Прежде чем
я закончу, я должен еще раз выразить восхищение, которое я чувствую по поводу неожиданного тождества таутохроны Гюйгенса и моей брахистохроны. Я считаю особенно замечательным то, что это совпадение может иметь место только при выполнении гипотезы Галилея, так что мы даже получаем из этого доказательство его правоты. Природа всегда стремится действовать самым простым способом, и поэтому здесь позволяет одной кривой выполнять две различные функции, в то время как при любом другом предположении нам понадобились бы две кривые…’’
Слайд 15Методы, которые братья разработали для решения задач и которые они оспаривали
друг у друга, были обобщены Эйлером в Methodus inveniendi lineascurvas maximi minimive proprietate gaudentes sive solutio problematis isoperimetrici latissimo sensu accepti, опубликованных в 1744 году. В этой работе, русская версия названия которой “Метод нахождения плоских кривых, показывающий некоторые свойства максимумов и минимумов”, Эйлер обобщает задачи, исследованные братьями Бернулли, но сохраняет геометрический подход, разработанный Иоганном Бернулли для их решения. Он обнаружил то, что сейчас известно как уравнения Эйлера-Лагранжа для поиска стационарных точек и экстремумов функционалов.
Слайд 16Идея состоит в нахождении функции, на которой достигается максимум или минимум
определенной величины, удовлетворяющей некоторым ограничениям. Например, Иоганн Бернулли перед Эйлером поставил определенные геодезические задачи, которые, как и задача о брахистохроне, были такого типа. Здесь задача состояла в нахождении кривых наименьшей длины, лежащих на данной поверхности. Эйлер, однако, отметил, что геометрический подход к таким задачам не был идеальным, и он давал только необходимые условия, которым должно удовлетворять решение. Вопрос о существовании решения не был решен Эйлером.
Слайд 17Лагранж в 1760 году опубликовал эссе о новом методе нахождения максимумов
и минимумов неопределенных интегральных формул. Он дал аналитический метод, применимый к задачам вариационного исчисления. Во введении к своей работе Лагранж приводит историческое развитие идей, целесообразным закончить, приведя слова Лагранжа, которые отражают в действительности все достижения:
“Первая задача этого типа [вариационного исчисления], которую решили математики – это задача о брахистохроне, или кривой наискорейшего спуска, предложенная Иоганном Бернулли в конце прошлого века. Ее решение было найдено рассмотрением частных случаев, и только спустя некоторое время, исследуя изопериметрические кривые, великий математик, о котором мы говорим, и его знаменитый брат Якоб Бернулли дали некоторые общие правила для решения ряда других задач того же типа. Поскольку, однако, правила не были достаточно общими, знаменитый Эйлер взял на себя задачу сведения всех этих исследований в общий метод, который он привел в своем “Рассуждении о новом методе определения максимумов и минимумов неопределенных интегральных формул’’ – оригинальной работе, в которой освещена глубокая наука исчисления. Тем не менее, несмотря на то что метод гениальный и мощный, надо признать, что он не так прост, как можно было бы надеяться в работе по чистому анализу…’’
“Первая задача этого типа [вариационного исчисления], которую решили математики – это задача о брахистохроне, или кривой наискорейшего спуска, предложенная Иоганном Бернулли в конце прошлого века. Ее решение было найдено рассмотрением частных случаев, и только спустя некоторое время, исследуя изопериметрические кривые, великий математик, о котором мы говорим, и его знаменитый брат Якоб Бернулли дали некоторые общие правила для решения ряда других задач того же типа. Поскольку, однако, правила не были достаточно общими, знаменитый Эйлер взял на себя задачу сведения всех этих исследований в общий метод, который он привел в своем “Рассуждении о новом методе определения максимумов и минимумов неопределенных интегральных формул’’ – оригинальной работе, в которой освещена глубокая наука исчисления. Тем не менее, несмотря на то что метод гениальный и мощный, надо признать, что он не так прост, как можно было бы надеяться в работе по чистому анализу…’’