- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по теме: Симметрия в пространстве
Содержание
- 1. Презентация по теме: Симметрия в пространстве
- 2. Симметрия в пространстве «Симметрия…есть идея, с помощью
- 3. Симметрия в пространстве. Точки и
- 4. Симметрия в пространстве. Точки и
- 5. Симметрия в пространстве. Ежедневно каждый из
- 6. Симметрия в пространстве. Немецкий философ Иммануил Кант
- 7. Симметрия в пространстве.Точки и
- 8. Центр, ось, плоскость симметрии. Точка
- 9. Симметрия в природе. «Раз, стоя перед чёрной
- 10. Симметрия в природе. Все организмы, растущие в
- 11. Симметрия в искусстве. Прекрасные образцы симметрии демонстрируют
- 12. Симметрия в искусстве.Кижи. Церковь Преображения.Мозаика собора Св. Софии в Киеве (1043-1046)
- 13. Правильные многогранники. В геометрии фигура может иметь
- 14. Правильные многогранники. Примером правильного многогранника является куб.
- 15. 1.Правильный тетраэдр. Тетра – «4» - четырёхугольник.Центра симметрии нет.Осей симметрии – 3.Плоскостей симметрии – 6.
- 16. 2.Правильный гексаэдр (куб). Гекса – «6» -
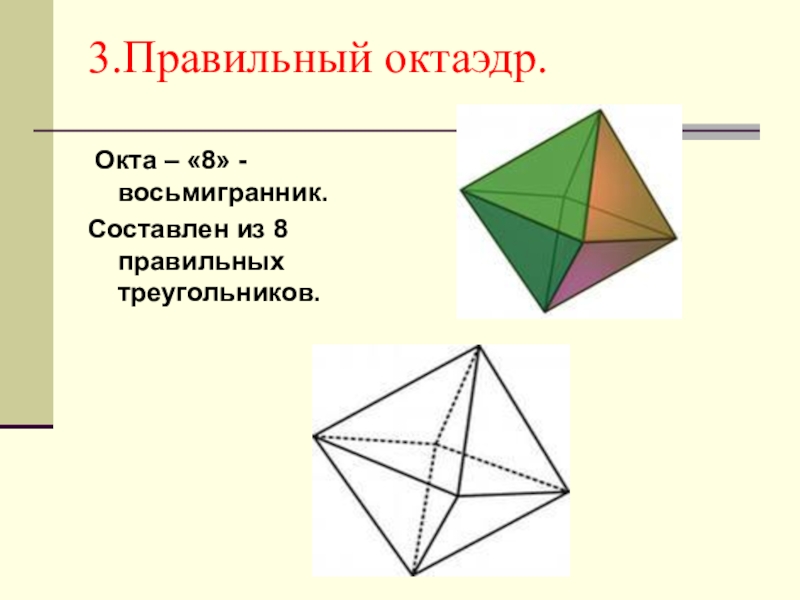
- 17. 3.Правильный октаэдр. Окта – «8» - восьмигранник.Составлен из 8 правильных треугольников.
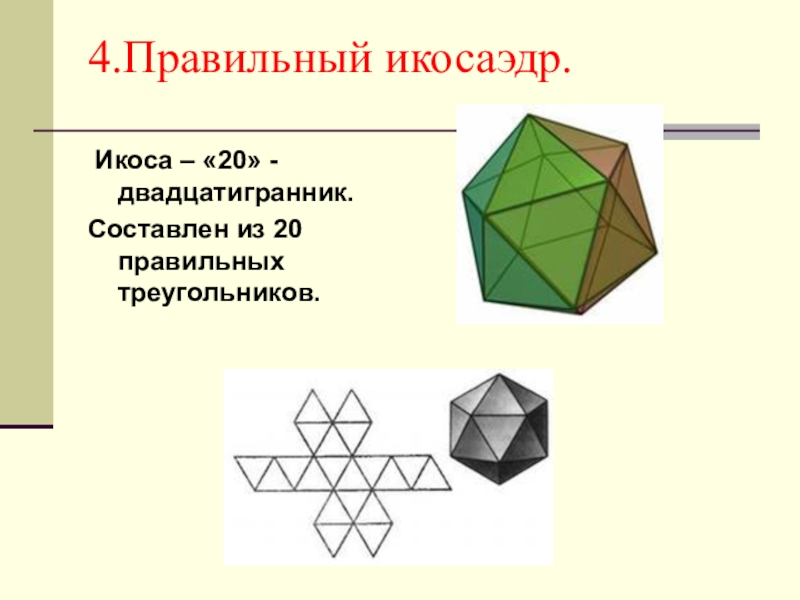
- 18. 4.Правильный икосаэдр. Икоса – «20» - двадцатигранник.Составлен из 20 правильных треугольников.
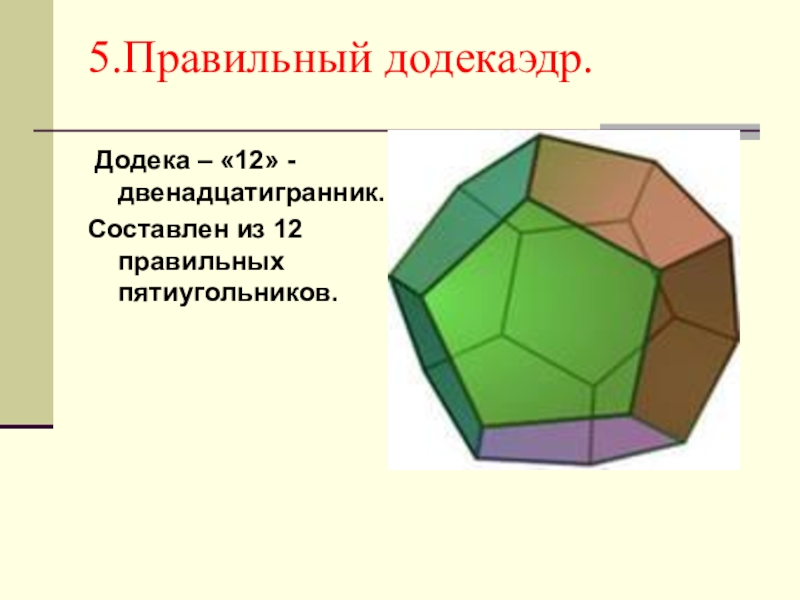
- 19. 5.Правильный додекаэдр. Додека – «12» - двенадцатигранник.Составлен из 12 правильных пятиугольников.
- 20. Правильные многогранники
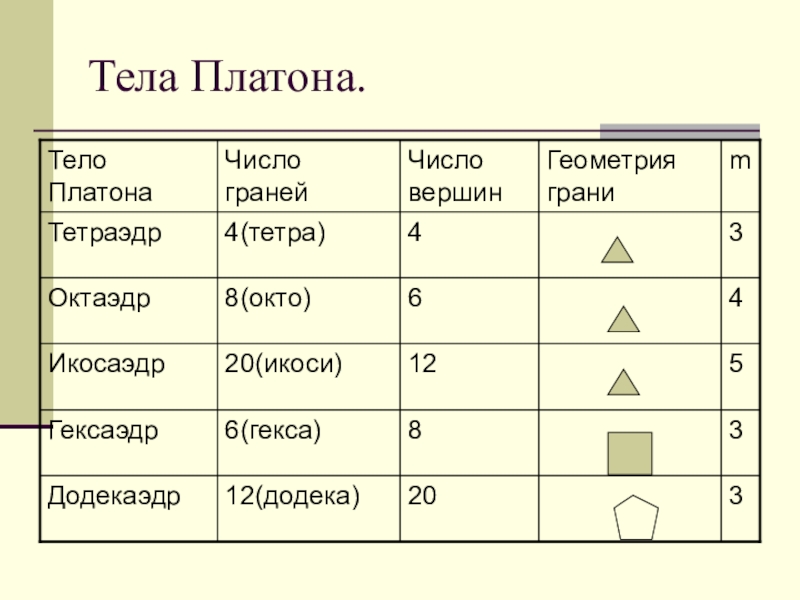
- 21. Тела Платона.
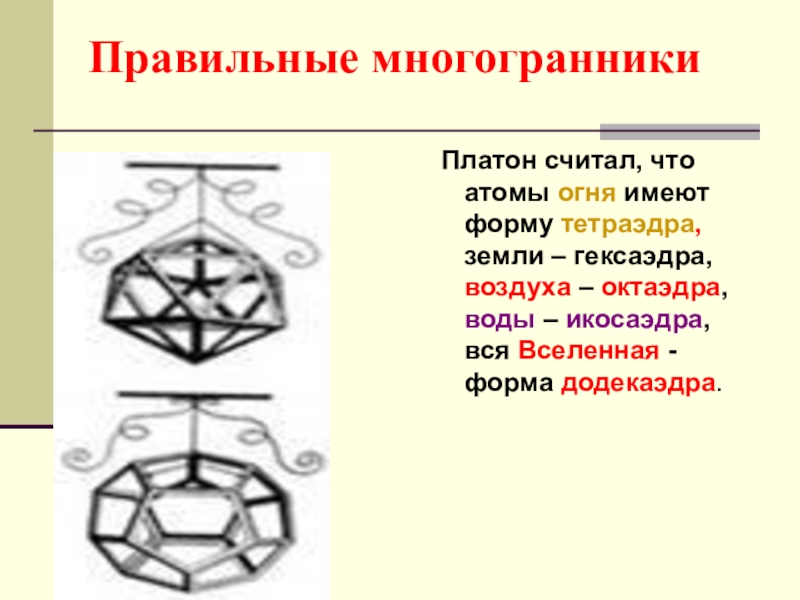
- 22. Правильные многогранники Платон считал, что атомы огня
- 23. Правильные многогранники Сальвадор Дали «Тайная вечере».Герои сидят на фоне огромного додекаэдра
- 24. Правильные многогранники Дюрер. Меланхолия (гравюра)В эпоху Возрождения
Слайд 1Симметрия в пространстве.
Понятие правильного многогранника.
Элементы симметрии правильных многогранников.
Слайд 2Симметрия в пространстве
«Симметрия…есть идея, с помощью которой человек веками пытался
математик Герман Вейль (1885 – 1955)
В планиметрии мы рассматривали фигуры, симметричные относительно точки и прямой. В стереометрии рассматривают симметрию относительно точки, прямой и плоскости.
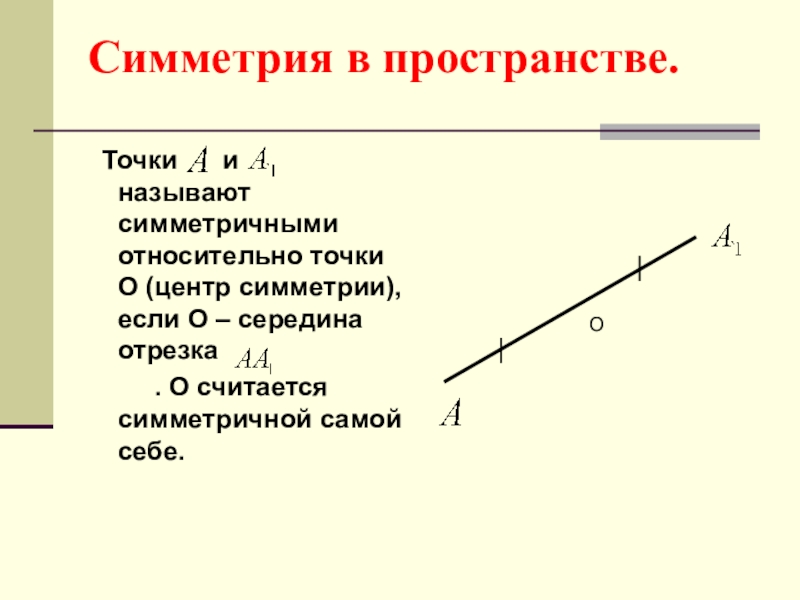
Слайд 3Симметрия в пространстве.
Точки и
. О считается симметричной самой себе.
О
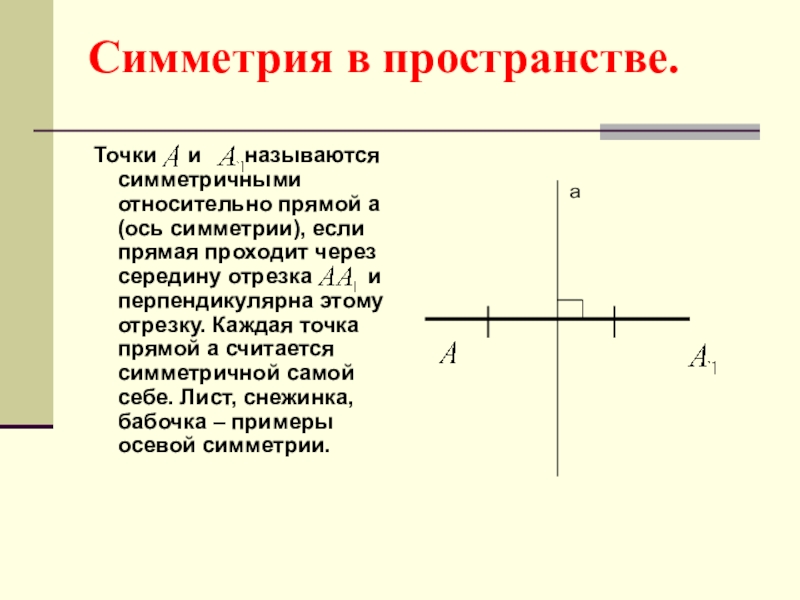
Слайд 4Симметрия в пространстве.
Точки и называются
а
Слайд 5Симметрия в пространстве.
Ежедневно каждый из нас по несколько раз
Слайд 6Симметрия в пространстве.
Немецкий философ Иммануил Кант (1724-1804) говорил о зеркальном
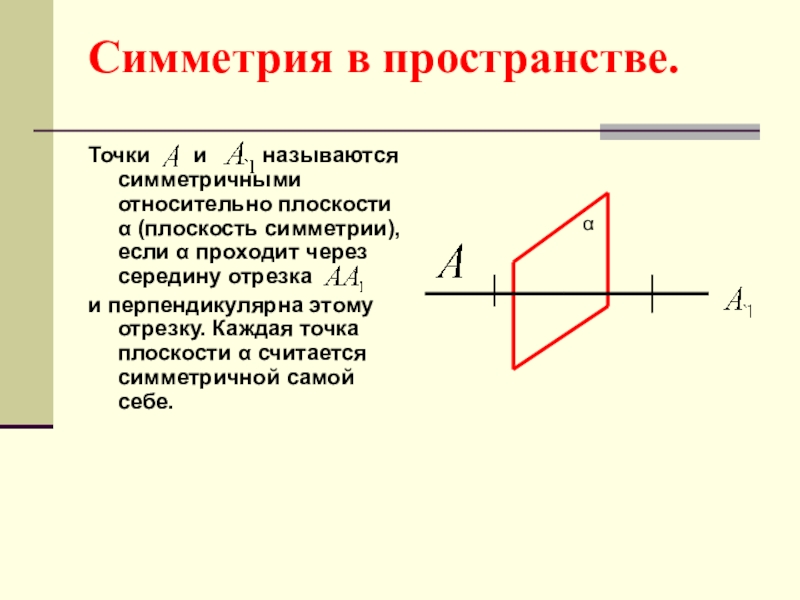
Слайд 7Симметрия в пространстве.
Точки и
и перпендикулярна этому отрезку. Каждая точка плоскости α считается симметричной самой себе.
α
Слайд 8Центр, ось, плоскость симметрии.
Точка (прямая, плоскость) называется центром
Если фигура имеет центр (ось, плоскость) симметрии, то говорят, что она обладает центральной ( осевой, зеркальной) симметрией.
Слайд 9Симметрия в природе.
«Раз, стоя перед чёрной доской и рисуя на
Л. Толстого
Господство симметрии в природе объясняется силой тяготения, действующей во Вселенной. Действием тяготения или отсутствием такового объясняется то, что и космические тела, плавающие во Вселенной, и микроорганизмы, взвешенные в воде, обладают высшей формой симметрии – сферической ( при любом повороте относительно центра фигура совпадает сама с собой).
Слайд 10Симметрия в природе.
Все организмы, растущие в прикреплённом состоянии (деревья) или
Для животных, способных передвигаться в воде, воздухе или по земле, кроме направления силы тяжести, важным оказывается и направление движения. Такие животные имеют плоскость симметрии. Биологи эту плоскость симметрии называют биларетальной, и тип симметрии – зеркальным.
Почти все кристаллы в природе – симметричны.
Слайд 11Симметрия в искусстве.
Прекрасные образцы симметрии демонстрируют произведения искусства: архитектура, живопись
Церковь Покрова на Нерли
( Владимировская область)
Слайд 12Симметрия в искусстве.
Кижи. Церковь Преображения.
Мозаика собора Св. Софии в Киеве
(1043-1046)
Слайд 13Правильные многогранники.
В геометрии фигура может иметь один или несколько центров
Слайд 14Правильные многогранники.
Примером правильного многогранника является куб.
Не существует правильного многогранника,
При n ≥ 6 угол каждого многоугольника больше или равен 120˚. Но, при каждой вершине многогранника должно быть не менее трёх плоских углов, т.е. 120˚*3=360˚.
По этой же причине каждая вершина правильного многогранника может быть вершиной 3, 4, 5 правильных треугольников, 3 квадратов или 3 правильных пятиугольников. Значит, есть только 5 правильных многогранников.
Слайд 151.Правильный тетраэдр.
Тетра – «4» - четырёхугольник.
Центра симметрии нет.
Осей симметрии –
Плоскостей симметрии – 6.
Слайд 162.Правильный гексаэдр (куб).
Гекса – «6» - шестигранник.
Центр симметрии – точка
Осей симметрии – 9.
Плоскостей симметрии – 9.
Слайд 184.Правильный икосаэдр.
Икоса – «20» - двадцатигранник.
Составлен из 20 правильных треугольников.
Слайд 195.Правильный додекаэдр.
Додека – «12» - двенадцатигранник.
Составлен из 12 правильных пятиугольников.
Слайд 20Правильные многогранники
Правильные многогранники
Подробно описал свойства правильных многогранников древнегреческий учёный Платон. Поэтому их называют телами Платона.
Правильным многогранникам посвящена XIII книга «Начал» Евклида.
Слайд 22Правильные многогранники
Платон считал, что атомы огня имеют форму тетраэдра, земли
Слайд 23Правильные многогранники
Сальвадор Дали «Тайная вечере».
Герои сидят на фоне огромного
додекаэдра
Слайд 24Правильные многогранники
Дюрер. Меланхолия (гравюра)
В эпоху Возрождения меланхолический
темперамент отождествляли с
началом. На гравюре Дюрера
Меланхолия окружена атрибутами
зодчества и геометрии, отчего
математики любят считать этот
шедевр графического искусства
олицетворением духа математики, а саму Меланхолию – представительницей
математики в мире прекрасного.