я запомню.
Вовлеки меня, и я научусь.
- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по теме Производная
Содержание
- 1. Презентация по теме Производная
- 2. Содержание диктанта
- 3. Задача №1.Найти промежутки возрастания и убывания функции
- 4. Задача №3.Составить уравнение касательной к графику функции
- 5. Карточка 11. Расшифруйте, как И. Ньютон называл производную функцию.
- 6. Карточка 21. Решив эти примеры, вы расшифруете фамилию французского математика, который ввел термин .
- 7. Карточка 31. Решив эти примеры, вы узнаете, как И. Ньютон называл функцию
- 8. Карточка 41. Решив эти примеры, вы узнаете
- 9. Производная и ее применениеГеометрический смысл производной заключается
- 10. Алгоритм нахождения уравнения касательной к графику функции
- 11. Вторая производная Физический смысл производной
- 12. Исследование функции монотонность
- 13. Экстремумы Необходимое условие экстремума Достаточное условие экстремума
- 14. Алгоритм нахождения интервалов монотонности и экстремумов
- 15. Наибольшее и наименьшее значения функции Алгоритм
- 16. Применение производной к исследованию функции
- 17. Слайд 17
- 18. Спасибо за внимание !
Содержание диктанта
Слайд 3Задача №1.
Найти промежутки возрастания и убывания функции у = lnх +
Задача №2.
Найти наибольшее значение функции
у = 19 – 2 cos х - на отрезке [- ]
Слайд 4Задача №3.
Составить уравнение касательной к графику функции f (х) = ln
(2е - х) в точке х0 = е
Задача №4.
Тело движется по прямой так, что расстояние S до него от некоторой точки А этой прямой изменяется по закону
S = 0,5 t2 +3 t + 2, где t – время движения. Через какое время после начала движения скорость тела окажется равной 15м/с?
Слайд 6Карточка 2
1. Решив эти примеры, вы расшифруете фамилию французского математика, который
ввел термин <производная>.
Слайд 8Карточка 4
1. Решив эти примеры, вы узнаете фамилию ученого, который вывел
формулы, связывающие тригонометрические функции с показательной
Слайд 9Производная и ее применение
Геометрический смысл производной заключается в том, что значение
производной функции в точке х равно угловому коэффициенту касательной к графику функции в точке (х, f (x))
Уравнение касательной к графику функции y = f (х) в точке х0:
у = f (х0) + f ' (х0)(х-х0)
Уравнение касательной к графику функции y = f (х) в точке х0:
у = f (х0) + f ' (х0)(х-х0)
Слайд 15Наибольшее и наименьшее значения функции
Алгоритм нахождения наибольшего и наименьшего значений функции,
непрерывной на отрезке
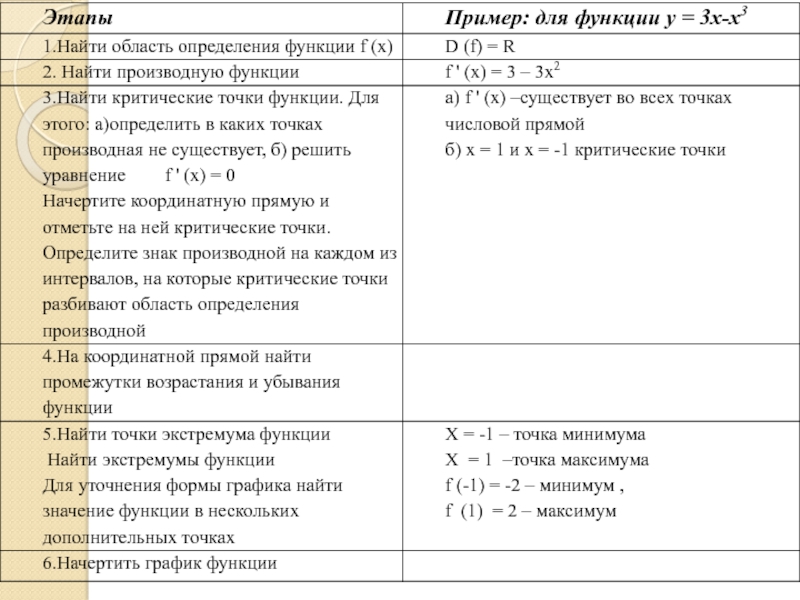
Слайд 16 Применение производной
к исследованию функции
Схема исследования функции
При исследовании свойств
функции полезно найти:
- область ее определения;
- производную;
- критические точки;
- промежутки возрастания и убывания;
- точки экстремума и значения функции в этих точках.
- область ее определения;
- производную;
- критические точки;
- промежутки возрастания и убывания;
- точки экстремума и значения функции в этих точках.