- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по теме Повторение_9 класс_Дискретная математика
Содержание
- 1. Презентация по теме Повторение_9 класс_Дискретная математика
- 2. I. Теория множеств (Основоположник: Г.Кантор)1. А={1; 2;
- 3. 2. В классе учатся 40 человек. Из
- 4. Логические операции01010011Инверсия1100Конъюнкция0001Дизъюнкция0111Импликация1101Эквиваленция1001Порядок вычислений:(), ¬, ∧, ∨, →, ↔II. Логика (Основоположники: Аристотель, Д. Буль)Законы алгебры логики
- 5. Слайд 5
- 6. 3. Составить таблицу истинности для формулы:¬(B ∧
- 7. 4. Упростите логическое выражение:а) ¬(B ∧ C) ∨ (A∧C ⇒ B)Решение:Ответ: 1
- 8. 4. Упростите логическое выражение:б) (A v B
- 9. 5. Для какого имени истинно высказывание:¬ (Первая
- 10. 6. Символом F обозначено одно из указанных
- 11. 7. Укажите, какое логическое выражение равносильно выражению
- 12. 8 (а). Три друга обсуждали историю Нового
- 13. 8 (б). На новогодний праздник три друга
- 14. 9. Известно, что на одной двери надпись
- 15. III. Комбинаторика (Основоположники: Б. Паскаль, Г. Лейбниц) Комбинаторные соединения
- 16. Соединения n элементов из n с учётом
- 17. 10. Сколькими способами можно составить расписание одного
- 18. 11. В 10 «Б» классе 32 учащихся.
- 19. 12. Сколько существует различных двузначных чисел, в
- 20. 13. Вычислить: 6! -5!1) 600 2) 300 3) 1 4)
- 21. IV. Теория вероятностей (Основоположники: Б. Паскаль,
- 22. 15. Монету бросили три раза. Какова вероятность
- 23. 16. В денежно-вещевой лотерее на 1000000 билетов
- 24. V. Математическая статистика (Термин «статистика» ввел Г.
- 25. Домашнее задание*«ДЗ_Повторение 9 kl [ДМ].doc»
Слайд 1Эхо часто прекраснее голоса, которое оно повторяет.
Оскар Уайльд
Лавлинский М.В., LavlinskiMV@mail.ru
Слайд 2I. Теория множеств (Основоположник: Г.Кантор)
1. А={1; 2; 3; 4; 5}, В={1;
Найдите: А∩B, А∪B, А\B, АΔB, А∩С, A\C, АΔС
Решение:
Пересечение множеств (A∩B={ x | x∈A и x∈B })
А∩B = {1; 2; 3}
Объединение множеств (A∪B={x|x∈A или x∈B })
А∪B= {1; 2; 3; 4; 5; a; b; c}
Разность множеств (A\B={ x | x∈A и x∉B })
А\B= {4; 5}
Симметрическая разность (A∆B=(A\B)∪(B\A))
АΔB= {4; 5; a; b; c}
5) А∩С= ∅
6) A\C= {1; 2; 3; 4; 5}
7) АΔС= {1; 2; 3; 4; 5; a; b; c}
Слайд 32. В классе учатся 40 человек. Из них по русскому языку
19
Ответ: 4, 12
Решение:
Дано: n(U)= 40
n(Р)= 19, n(М)= 17, n(И)= 22
n(Р\(М ∪ И)) = 4
n(М\(Р ∪ И)) = 4
n(И\(М ∪ Р)) = 11
n(М ∩ И) = 7
n(Р ∩ М ∩ И) = 5
Найти:
n(U\(Р ∪ М ∪ И))
n((М∩И)\(Р∩М∩И))
n((Р∩И)\(Р∩М∩И))
n((М∩Р)\(Р∩М∩И))
17
22
4
4
11
5
2
6
4
n(Р ∪ М ∪ И)=
4+6+4+4+5+2+11= 36
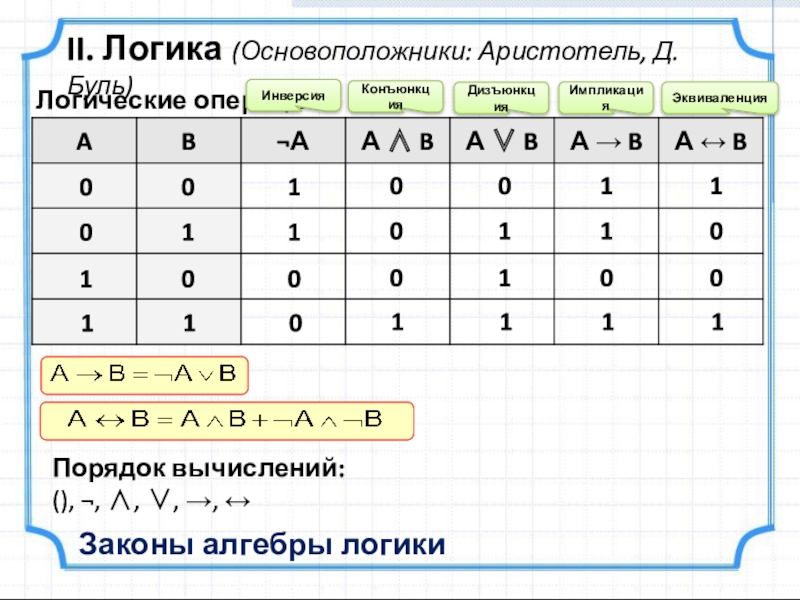
Слайд 4Логические операции
0
1
0
1
0
0
1
1
Инверсия
1
1
0
0
Конъюнкция
0
0
0
1
Дизъюнкция
0
1
1
1
Импликация
1
1
0
1
Эквиваленция
1
0
0
1
Порядок вычислений:
(), ¬, ∧, ∨, →, ↔
II. Логика (Основоположники: Аристотель,
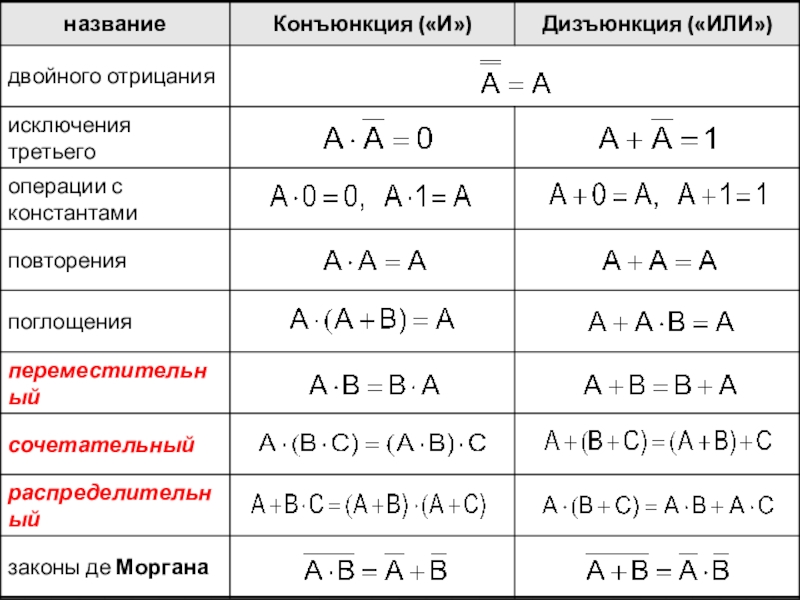
Законы алгебры логики
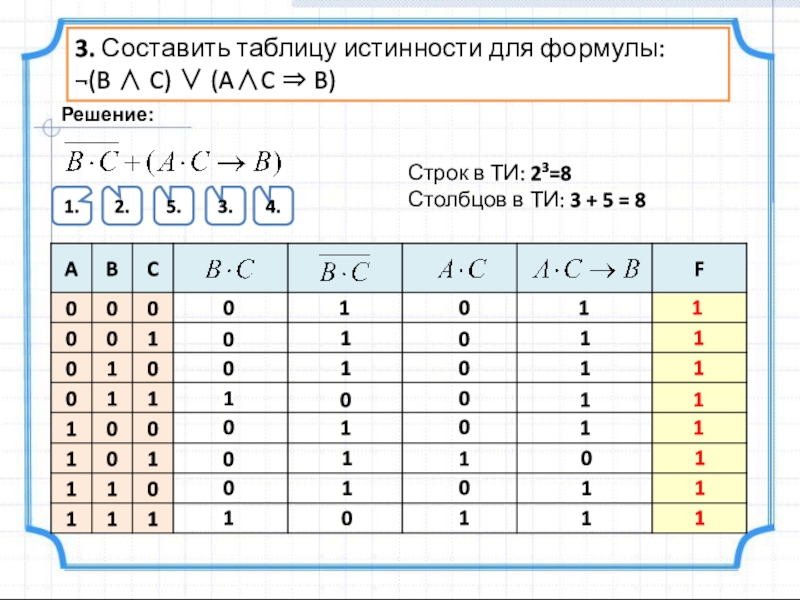
Слайд 63. Составить таблицу истинности для формулы:
¬(B ∧ C) ∨ (A∧C ⇒
Решение:
1.
2.
3.
4.
5.
Строк в ТИ: 23=8
Столбцов в ТИ: 3 + 5 = 8
0
0
0
1
0
0
0
1
1
1
1
0
1
1
1
0
0
0
0
0
0
1
0
1
1
1
1
1
1
0
1
1
1
1
1
1
1
1
1
1
Слайд 84. Упростите логическое выражение:
б) (A v B v C) & (A
Решение:
Ответ:
Слайд 95. Для какого имени истинно высказывание:
¬ (Первая буква имени гласная ->
1) ЕЛЕНА
2) ВАДИМ
3) АНТОН
4) ФЕДОР
Решение:
¬ (Первая буква имени гласная -> Четвертая буква имени согласная)
≡
¬ (¬(Первая буква имени гласная) ∨ (Четвертая буква имени согласная))
≡
(Первая буква имени гласная) ∧ ¬(Четвертая буква имени согласная))
Ответ: 3) Антон
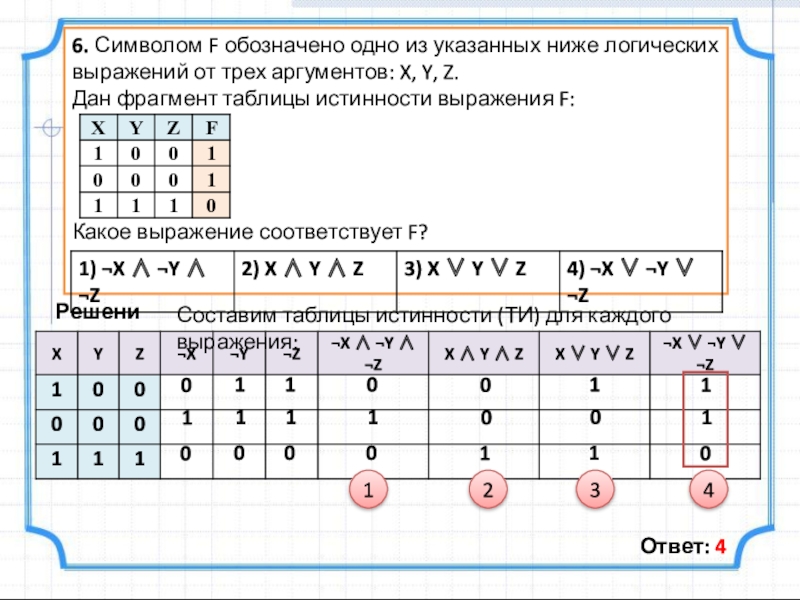
Слайд 106. Символом F обозначено одно из указанных ниже логических выражений от
Дан фрагмент таблицы истинности выражения F:
Какое выражение соответствует F?
Решение:
Составим таблицы истинности (ТИ) для каждого выражения:
1
2
3
4
0
1
0
1
1
0
1
1
0
0
1
0
0
0
1
1
0
1
1
1
0
Ответ: 4
Слайд 117. Укажите, какое логическое выражение равносильно выражению
A ∧ ¬(¬B ∨
Решение:
A ∧ ¬(¬B ∨ C)
= A ∧ ¬¬B ∧ ¬C
= A ∧ B ∧ ¬C
Ответ: 3
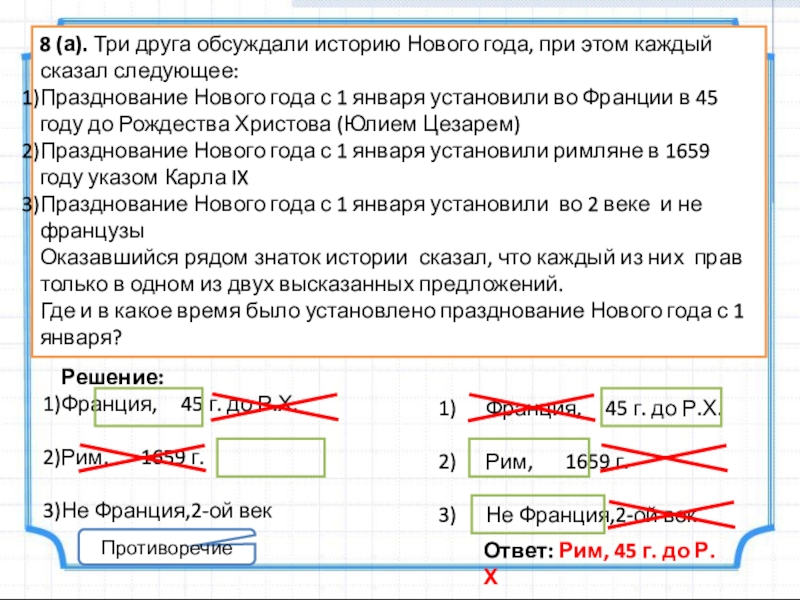
Слайд 128 (а). Три друга обсуждали историю Нового года, при этом каждый
Празднование Нового года с 1 января установили во Франции в 45 году до Рождества Христова (Юлием Цезарем)
Празднование Нового года с 1 января установили римляне в 1659 году указом Карла IX
Празднование Нового года с 1 января установили во 2 веке и не французы
Оказавшийся рядом знаток истории сказал, что каждый из них прав только в одном из двух высказанных предложений.
Где и в какое время было установлено празднование Нового года с 1 января?
Решение:
Франция, 45 г. до Р.Х.
Рим, 1659 г.
Не Франция,2-ой век
Противоречие
Франция, 45 г. до Р.Х.
Рим, 1659 г.
Не Франция,2-ой век
Ответ: Рим, 45 г. до Р.Х
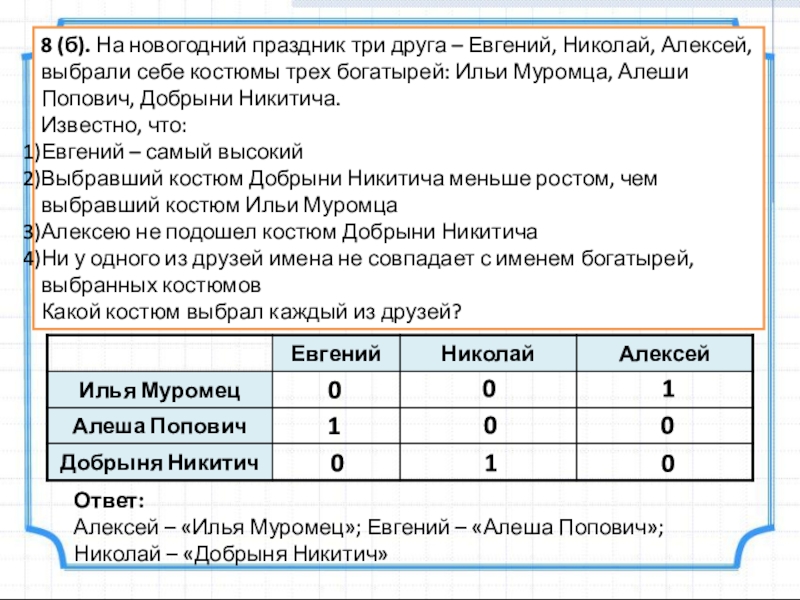
Слайд 138 (б). На новогодний праздник три друга – Евгений, Николай, Алексей,
Известно, что:
Евгений – самый высокий
Выбравший костюм Добрыни Никитича меньше ростом, чем выбравший костюм Ильи Муромца
Алексею не подошел костюм Добрыни Никитича
Ни у одного из друзей имена не совпадает с именем богатырей, выбранных костюмов
Какой костюм выбрал каждый из друзей?
0
0
1
0
0
0
1
Ответ:
Алексей – «Илья Муромец»; Евгений – «Алеша Попович»;
Николай – «Добрыня Никитич»
0
1
Слайд 149. Известно, что на одной двери надпись истинна, а на другой
Если надпись на первой двери - "за этой дверью есть подарок", а на второй двери - «подарок за обоими дверьми", то:
1) подарок за обоими дверьми;
2) подарок только за второй дверью;
3) подарка нет ни за одной дверью;
4) подарок только за первой дверью;
5) определенно место подарка установить нельзя.
Выберите вариант ответа
Ответ: Подарок только за первой дверью
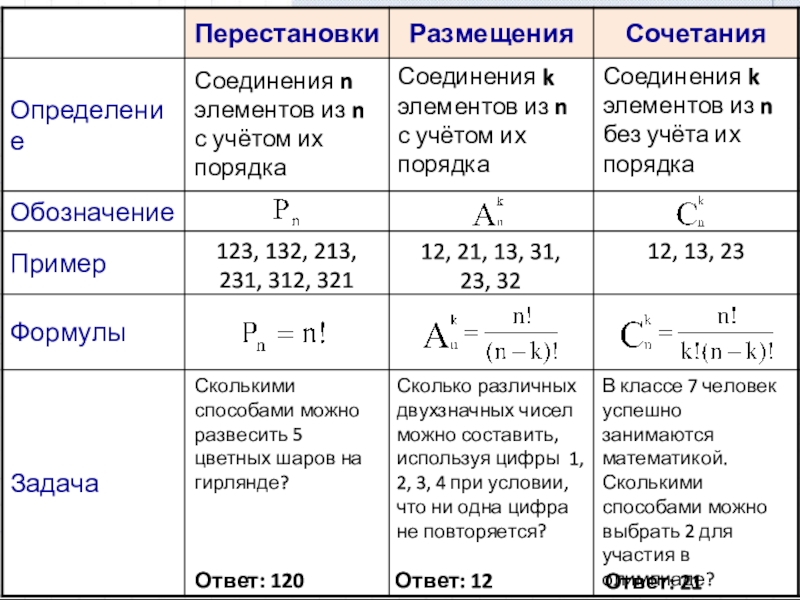
Слайд 16Соединения n элементов из n с учётом их порядка
Соединения k элементов
Соединения k элементов из n без учёта их порядка
123, 132, 213, 231, 312, 321
12, 21, 13, 31,
23, 32
12, 13, 23
Сколькими способами можно развесить 5 цветных шаров на гирлянде?
Ответ: 120
Сколько различных двухзначных чисел можно составить, используя цифры 1, 2, 3, 4 при условии, что ни одна цифра не повторяется?
Ответ: 12
В классе 7 человек успешно занимаются математикой. Сколькими способами можно выбрать 2 для участия в олимпиаде?
Ответ: 21
Слайд 1710. Сколькими способами можно составить расписание одного учебного дня из 5
1) 30 2) 100 3) 120 4) 5
Решение:
1-ый способ (правило произведения):
5 ⋅ 4 ⋅ 3 ⋅ 2 ⋅ 1 = 120
2-ой способ (формула):
Pn = n! – число перестановок
P5 = 5! = 120
Ответ: 120 (3)
Слайд 1811. В 10 «Б» классе 32 учащихся. Сколькими способами можно сформировать
1) 128 2) 35960 3) 36 4) 46788
Решение:
Ответ: 35960 (2)
Слайд 1912. Сколько существует различных двузначных чисел, в записи которых можно использовать
1) 10 2) 60 3) 20 4) 30
Решение:
1-ый способ (правило произведения):
6 ⋅ 5 = 30
2-ой способ (формула):
Ответ: 30 (4)
Слайд 2013. Вычислить: 6! -5!
1) 600 2) 300 3) 1 4) 1000
0! = 1
1! =
2! = 2
3! = 6
4! = 24
5! = 120
6! = 720
7! = 5040
8! = 40320
9! = 362880
10! = 3628800
Решение:
6! -5! =
720 – 120 = 600
Ответ: 600 (1)
Слайд 21IV. Теория вероятностей
(Основоположники: Б. Паскаль, П. Ферма, Х. Гюйгенс
14. В
Дано:
n = 43
m = 17
Найти:
P - ?
Решение:
P = m / n
n – общее количество исходов
m - количество благоприятных
P = 17 / 43
Ответ: 17/43 (2)
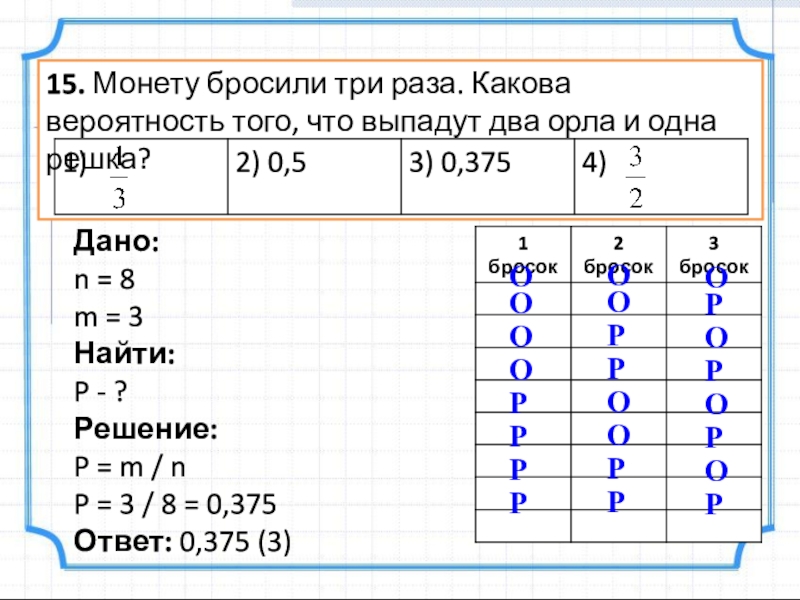
Слайд 2215. Монету бросили три раза. Какова вероятность того, что выпадут два
Дано:
n = 8
m = 3
Найти:
P - ?
Решение:
P = m / n
P = 3 / 8 = 0,375
Ответ: 0,375 (3)
О
О
О
О
О
О
Р
Р
Р
Р
Р
Р
Р
Р
Р
Р
Р
Р
О
О
О
О
О
О
Слайд 2316. В денежно-вещевой лотерее на 1000000 билетов разыгрывается 1200 вещевых и
Дано:
n = 1000000
m = 2000
Найти:
P - ?
Решение:
P = m / n
P = 2000 / 1000000
Ответ: 0,002 (4)
Слайд 24V. Математическая статистика
(Термин «статистика» ввел Г. Ахенвалль (1746))
17. Найдите медиану ряда
Решение:
Упорядочим выборку:
1, 2, 5, 7, 8, 9, 11, 12, 17
Ответ: 8
















![Презентация по теме Повторение_9 класс_Дискретная математика Домашнее задание*«ДЗ_Повторение 9 kl [ДМ].doc» Домашнее задание*«ДЗ_Повторение 9 kl [ДМ].doc»](/img/thumbs/4cf4ef306f33cc4b8e9082a137441389-800x.jpg)





