- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по теме Площадь трапеции
Содержание
- 1. Презентация по теме Площадь трапеции
- 2. Вопросы для самопроверкиДайте определение трапеции.Как найти площадь
- 3. Определение трапецииТрапеция – это четырехугольник, у которого
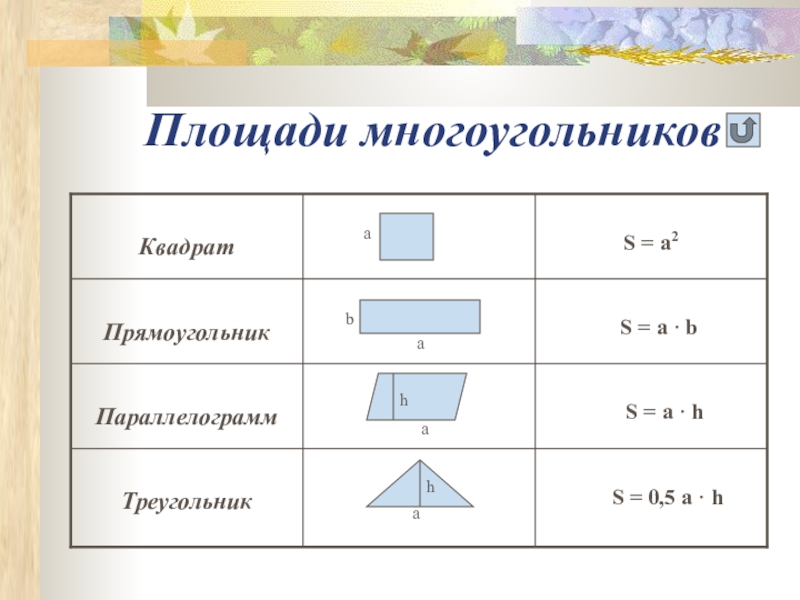
- 4. Площади многоугольников h h
- 5. Свойство площадей равных фигурРавные многоугольники имеют равные площади
- 6. Свойство площадейЕсли многоугольник составлен из нескольких многоугольников, то его площадь равна сумме площадей этих многоугольников
- 7. Отношение площадейЕсли угол одного треугольника равен углу
- 8. Работа в группах
- 9. Группа 1Начертите трапецию ABCD (BC // AD
- 10. Помощник для группы 1Четырехугольник ABCP – параллелограммСH–
- 11. Группа 2Начертите трапецию ABCD (BC // AD
- 12. Помощник для группы 2Четырехугольник BKDC- параллелограммBH– высота
- 13. Группа 3Начертите трапецию ABCD (BC // AD
- 14. Помощник для группы 3Четырехугольник ABKM – параллелограмм
- 15. Группа 4Начертите трапецию ABCD (BC // AD
- 16. Помощник для группы 4Рассмотрите треугольник ABC и
- 17. Площадь трапеции1 S = -2· ( a + b ) · h abh
- 18. Решите задачуНайдите площадь трапеции
- 19. Помощник для решения задачиДополнительное построение:
- 20. Домашнее задание:1. Высота трапеции равна меньшему
Слайд 2Вопросы для самопроверки
Дайте определение трапеции.
Как найти площадь квадрата?
Как найти площадь прямоугольника?
Как
Как найти площадь треугольника?
Сформулируй свойство площадей равных фигур.
Чему равна площадь многоугольника, составленного из нескольких многоугольников?
Как относятся площади треугольников, имеющих
по равному углу?
Слайд 3Определение трапеции
Трапеция – это четырехугольник, у которого две стороны параллельны, а
не параллельны.
Слайд 6Свойство площадей
Если многоугольник составлен из нескольких многоугольников, то его площадь равна
Слайд 7Отношение площадей
Если угол одного треугольника равен углу другого треугольника, то площади
a
b
m
c
S1
S2
Слайд 9Группа 1
Начертите трапецию ABCD (BC // AD ), в которой
Проведите дополнительное построение: достройте трапецию до параллелограмма со сторонами AB и BC (если возникли затруднения – обратитесь за помощь).
Найдите площадь трапеции, состоящую из параллелограмма ABCP, но без треугольника DCP (если возникли затруднения – обратитесь за помощью ).
Проверь правильность вывода формулы площади трапеции
Решите задачу
Слайд 10Помощник для группы 1
Четырехугольник ABCP – параллелограмм
СH– высота треугольника DCP является
Найдите площадь треугольника DCP
Найдите площадь параллелограмма ABCP
Найдите площадь трапеции ABCD как разность площадей его частей
A
B
C
D
P
H
Слайд 11Группа 2
Начертите трапецию ABCD (BC // AD ), в которой
Проведите дополнительное построение: через точку В проведите прямую BK // CD (если возникли затруднения – обратитесь за помощью ).
Найдите площадь трапеции, состоящую из треуголь- ника ABK и четырехугольника KBCD (если возникли затруднения – обратитесь за помощью ).
Проверь правильность вывода формулы площади трапеции
Решите задачу
Слайд 12Помощник для группы 2
Четырехугольник BKDC- параллелограмм
BH– высота треугольника ABK является и
Найдите площадь треугольника ABK
Найдите площадь параллелограмма BKDC
Найдите площадь трапеции ABCD как сумму площадей его частей
H
A
B C
D
K
Слайд 13Группа 3
Начертите трапецию ABCD (BC // AD ), в которой
Проведите дополнительное построение: «пристройте» к ABCD равную ей трапецию KMNP так, что точка C совпадает с точкой P, а точка D – с точкой N; отрезок MN лежит на прямой AD, а отрезок KP – на прямой BC (если возникли затруднения – обратитесь за помощью ).
Рассмотрите четырехугольник ABKM (определите его вид); найдите его площадь (если возникли затруднения – обратитесь за помощью ).
Найдите площадь трапеции ABCD (если возникли затруднения – обратитесь за помощью ).
Проверь правильность вывода формулы площади трапеции
Решите задачу
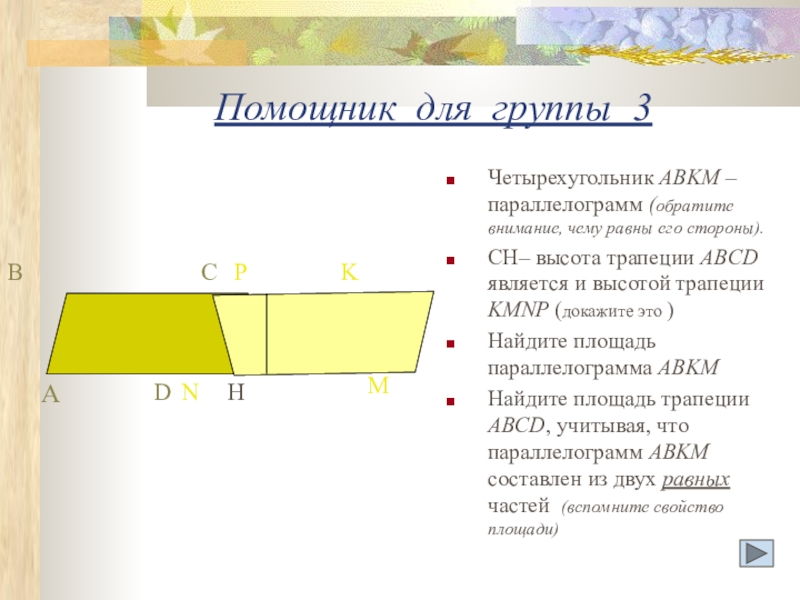
Слайд 14Помощник для группы 3
Четырехугольник ABKM – параллелограмм (обратите внимание, чему равны
СH– высота трапеции ABCD является и высотой трапеции KMNP (докажите это )
Найдите площадь параллелограмма ABKM
Найдите площадь трапеции ABCD, учитывая, что параллелограмм ABKM составлен из двух равных частей (вспомните свойство площади)
A
B
C
D
M
N
K
P
H
Слайд 15Группа 4
Начертите трапецию ABCD (BC // AD ), в которой
Проведите дополнительное построение: проведите диагональ AC (если возникли затруднения – обратитесь за помощью ).
Найдите площадь трапеции, состоящую из треуголь- ника ABC и треугольника ACD (если возникли затруднения – обратитесь за помощью ).
Проверь правильность вывода формулы площади трапеции
Решите задачу
Слайд 16Помощник для группы 4
Рассмотрите треугольник ABC и треугольник ACD
АH– высота треугольника
Найдите площадь треугольника ABC
Найдите площадь треугольника ACD
Найдите площадь трапеции ABCD как сумму площадей его частей
A
B
C
D
H
K
Слайд 18Решите задачу
Найдите площадь трапеции ABCD с
Выполните чертеж ( помощник - ).
Проведите дополнительное построение ( помощник - ).
Рассмотрите треугольник для нахождения высоты трапеции ( помощник - ).
Используя формулу, найдите площадь трапеции ( помощник - ).
Слайд 19Помощник для решения задачи
Дополнительное построение:
Рассмотрите прямоугольный треугольник AHD и найдите катет AH
(Внимание! В треугольнике есть угол 300)
Вспомните формулу для нахождения площади трапеции ( при необходимости вернитесь назад )
A
B
C
D
H
300
Слайд 20Домашнее задание:
1. Высота трапеции равна меньшему основанию и в два
2. В прямоугольной трапеции основания равны 22 см и 6 см, а большая боковая сторона – 20 см. Найдите площадь трапеции.