- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по теме Основы математической статистики
Содержание
- 1. Презентация по теме Основы математической статистики
- 2. I. Основные понятияСтатистика – это область науки,
- 3. Пример 1.В девятых классах «А» и «Б»
- 4. Общий ряд данныхВыборкаВариантаРяд данныхТо, откуда выбираютТо, что
- 5. Пример 1.В девятых классах «А» и «Б»
- 6. Пример 2. 30 абитуриентов на четырех вступительных
- 7. Пример 2. 30 абитуриентов на четырех вступительных
- 8. II. Графическое представление информацииАлгоритм получения графика распределения
- 9. Пример 3.Постройте график распределения и многоугольник частот
- 10. Многоугольник распределения кратностей
- 11. Многоугольник распределения частот
- 12. Многоугольник распределения частот (%)Чаще всего в практических приложениях используют многоугольники частот в процентах.
- 13. Построение гистограмм (столбчатых диаграмм) распределения:Разбиваем промежуток между
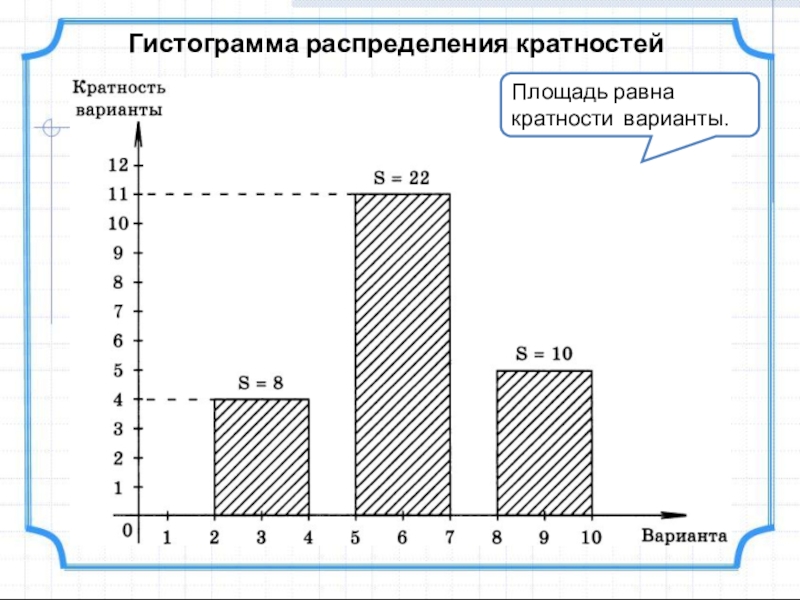
- 14. Гистограмма распределения кратностейПлощадь равна кратности варианты.
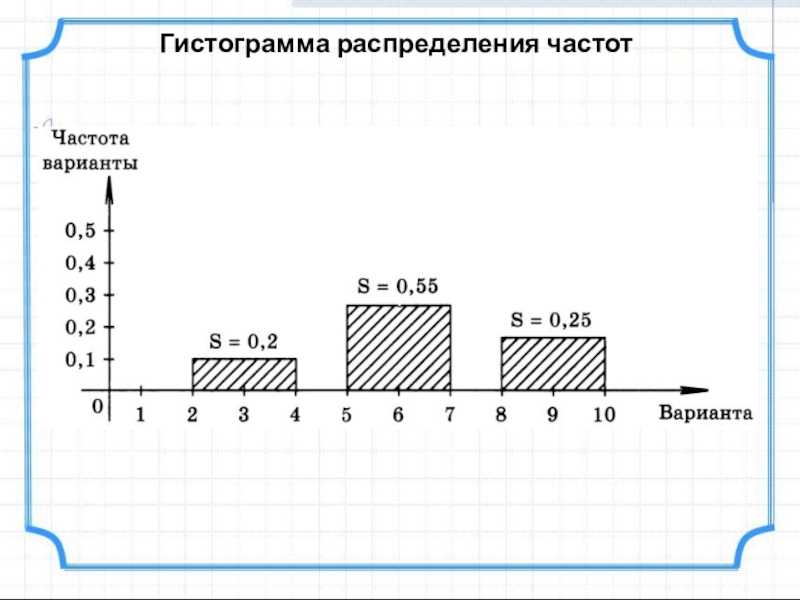
- 15. Гистограмма распределения частот
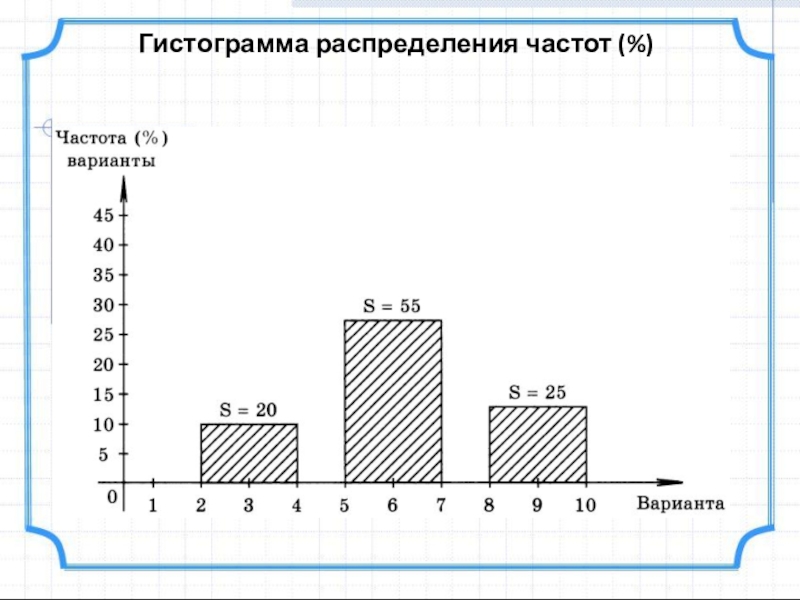
- 16. Гистограмма распределения частот (%)
- 17. «-» представления информации в виде гистограммТеряется первоначальная
- 18. III. Гистограммы распределения большого объёма информацииГистограммы незаменимы,
- 19. Пример 5. Произвели 500 измерений боковой ошибки
- 20. Пример 6. Измерялся размер 12000 бобов. По
- 21. Примеры взяты из различных областей, а графики
- 22. Гауссова кривая(кривая нормального распределения)Свойства:Симметрична относительно оси OyЕдинственный
- 23. Доска Гальтона (квинкункс, 1873 г.)Устройство для наглядной
- 24. IV. Числовые характеристики выборкиОбъемы выборок данных велики
- 25. Слайд 25
- 26. 3) Медиана (Me)(от лат. mediana – «среднее»)Медианой
- 27. Пример 7.Найдите среднее значение, размах и моду
- 28. Пример 8.В выборке 2, 7, 10, _,
- 29. Пример 9.Найдите медиану выборки:30, 32, 37, 40,
- 30. Пример 11.В ряду данных, состоящем из 12
- 31. 5) Среднее отклонение ( )Среднее
- 32. Пример 12.Вычислите среднее отклонение, дисперсию, среднее квадратичное
- 33. V. Экспериментальные данные и вероятности событийПример 13.
- 34. Бросил монету 4040 раз, и при этом
- 35. Статистическая устойчивость (СУ)При большом числе независимых повторений
- 36. Пример 14.Статистические исследования над литературными текстами показали,
- 37. Пример 15.До сегодняшнего дня не утихают споры
- 38. Пример 16.В середине 60-х годов в одной
- 39. Домашнее заданиеМАОУ Лицей ИГУ г. Иркутска, ligu.edu38.ru*КонспектСР «Основы математической статистики»«18_[ДЗ]Основы МС doc»
Слайд 1МАОУ Лицей ИГУ г. Иркутска,
ligu.edu38.ru
Лавлинский М.В., LavlinskiMV@mail.ru
К.Ф. Гаусс
(1777-1855)
Математика – царица наук!
1795
С этой работы математическая статистика
начинается как наука
Слайд 2I. Основные понятия
Статистика
– это область науки, изучающая сбор, анализ и
От лат. status - «состояние, положение вещей»
1746 г. – Г.Ахенваль ввел термин в науку
Слайд 3Пример 1.
В девятых классах «А» и «Б» измерили рост 50 учеников.
162, 168, 157, 176, 185, 160, 162, 158, 181, 179, 164, 176, 177, 180, 181, 179, 175, 180, 176, 165, 168, 164, 179, 163, 160, 176, 162, 178, 164, 190, 181, 178, 168, 165, 176, 178, 185, 179, 180, 168, 160, 176, 175, 177, 176, 165, 164, 177, 175, 181.
Недостатки данной информации:
Трудно «читается»
Не наглядна
Занимает много места
Другие задачи статистики:
получение и хранение информации
выработка различных прогнозов
оценка их достоверности
Выход:
— преобразовать данные, получить небольшое количество характеристик начальной информации.
⇒ Одна из основных задач статистики: обработка информации.
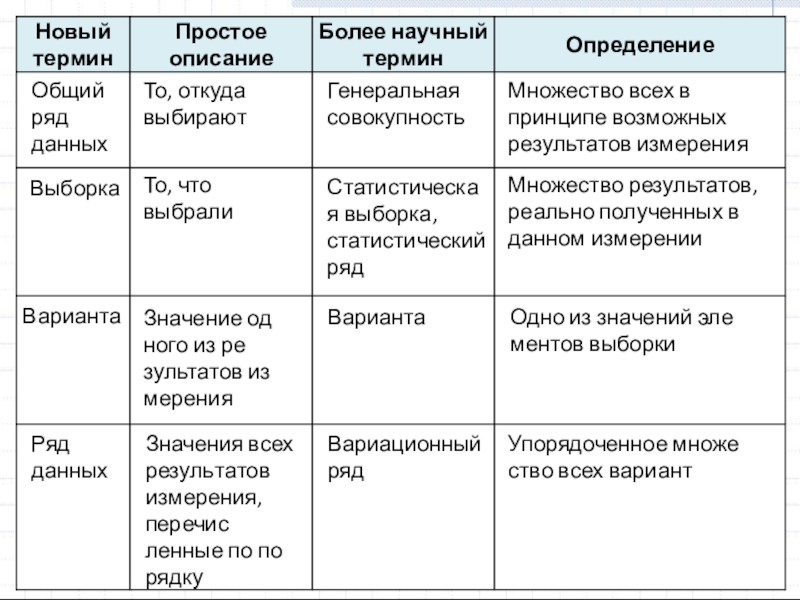
Слайд 4Общий ряд данных
Выборка
Варианта
Ряд данных
То, откуда выбирают
То, что выбрали
Значение одного из результатов
Значения всех результатов измерения, перечисленные по порядку
Генеральная совокупность
Статистическая выборка, статистический ряд
Варианта
Вариационный ряд
Множество всех в принципе возможных результатов измерения
Множество результатов, реально полученных в данном измерении
Одно из значений элементов выборки
Упорядоченное множество всех вариант
Слайд 5Пример 1.
В девятых классах «А» и «Б» измерили рост 50 учеников.
162, 168, 157, 176, 185, 160, 162, 158, 181, 179, 164, 176, 177, 180, 181, 179, 175, 180, 176, 165, 168, 164, 179, 163, 160, 176, 162, 178, 164, 190, 181, 178, 168, 165, 176, 178, 185, 179, 180, 168, 160, 176, 175, 177, 176, 165, 164, 177, 175, 181.
С некоторым запасом можно считать, что рост девятиклассника находится в пределах от 140 до 210 см.
⇒
Общий ряд данных этого измерения: 140; 141; 142; ...; 208; 209; 210
1.
Ряд данных — все реальные результаты измерения, выписанные в определенном порядке без повторений, например, по возрастанию:
157; 158; 160; 162; 163; 164; 165; 168; 175; 176; 177; 178; 179; 180; 181; 185; 190
Выборка — это данные реального измерения роста
(выписаны выше)
2.
3.
Варианта — это любое из чисел выборки
4.
Слайд 6Пример 2.
30 абитуриентов на четырех вступительных экзаменах набрали в сумме
20; 19; 12; 13; 16; 17; 15; 14; 16; 20; 15; 19; 20; 20; 15; 13; 19; 14; 18; 17; 12; 14; 12; 17; 18; 17; 20; 17; 16; 17.
Составьте общий ряд данных, выборку из результатов, стоящих на четных местах и соответствующий ряд данных.
Решение:
После получения двойки дальнейшие экзамены не сдаются, поэтому сумма баллов не может быть меньше 12 (12 — это 4 «тройки»). ⇒ Общий ряд данных: 12; 13; 14; 15; 16; 17; 18; 19; 20
Выборка состоит из 15 результатов: 19; 13; 17; 14; 20; 19; 20; ..., расположенных на четных местах
Ряд данных: 13; 14; 17; 19; 20
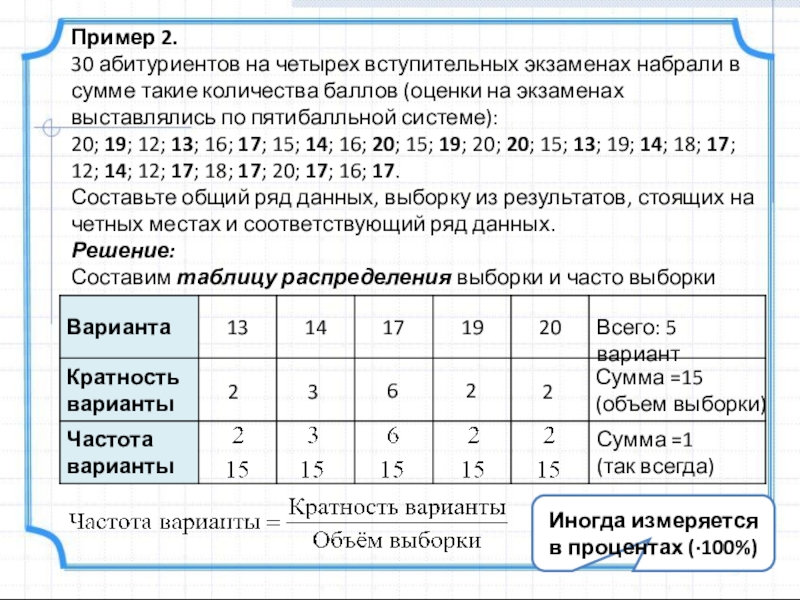
Составим таблицу распределения выборки и частот выборки
Слайд 7Пример 2.
30 абитуриентов на четырех вступительных экзаменах набрали в сумме
20; 19; 12; 13; 16; 17; 15; 14; 16; 20; 15; 19; 20; 20; 15; 13; 19; 14; 18; 17; 12; 14; 12; 17; 18; 17; 20; 17; 16; 17.
Составьте общий ряд данных, выборку из результатов, стоящих на четных местах и соответствующий ряд данных.
Решение:
Составим таблицу распределения выборки и часто выборки
2
3
6
2
2
Всего: 5 вариант
Сумма =15
(объем выборки)
Сумма =1
(так всегда)
Иногда измеряется в процентах (·100%)
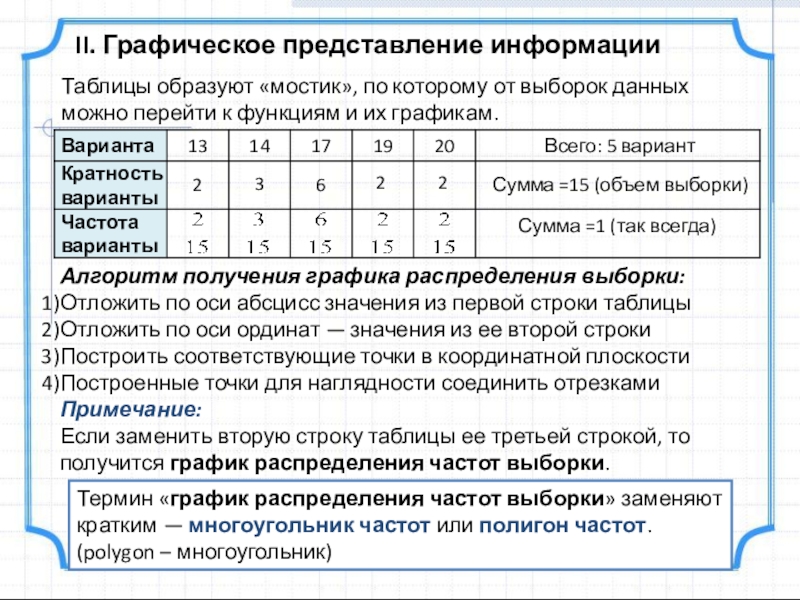
Слайд 8II. Графическое представление информации
Алгоритм получения графика распределения выборки:
Отложить по оси абсцисс
Отложить по оси ординат — значения из ее второй строки
Построить соответствующие точки в координатной плоскости
Построенные точки для наглядности соединить отрезками
Примечание:
Если заменить вторую строку таблицы ее третьей строкой, то получится график распределения частот выборки.
Таблицы образуют «мостик», по которому от выборок данных можно перейти к функциям и их графикам.
Пример 2.
2
3
6
2
2
Всего: 5 вариант
Сумма =15 (объем выборки)
Сумма =1 (так всегда)
Термин «график распределения частот выборки» заменяют кратким — многоугольник частот или полигон частот.
(polygon – многоугольник)
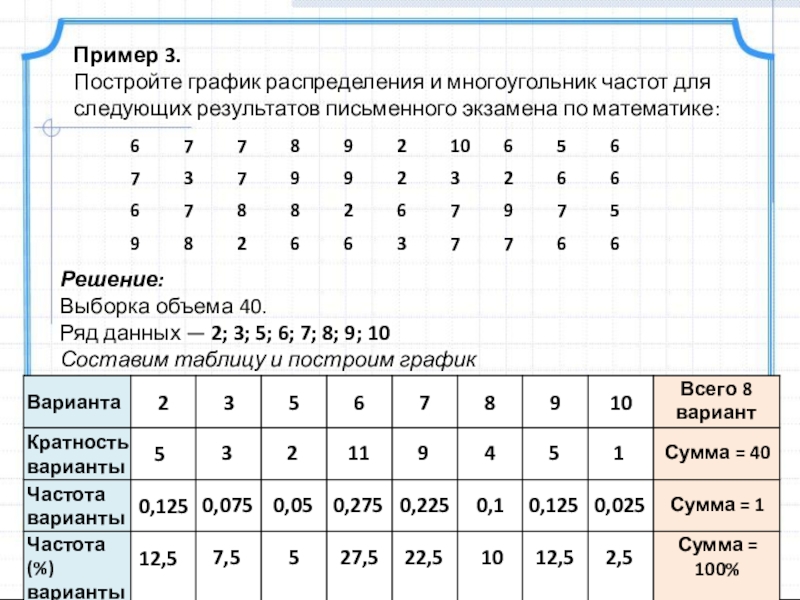
Слайд 9Пример 3.
Постройте график распределения и многоугольник частот для следующих результатов письменного
Решение:
Выборка объема 40.
Ряд данных — 2; 3; 5; 6; 7; 8; 9; 10
Составим таблицу и построим график
Всего 8 вариант
Сумма = 40
5
3
2
11
9
4
5
1
Сумма = 1
0,125
0,075
0,05
0,275
0,225
0,1
0,125
0,025
Сумма = 100%
12,5
7,5
5
27,5
22,5
10
12,5
2,5
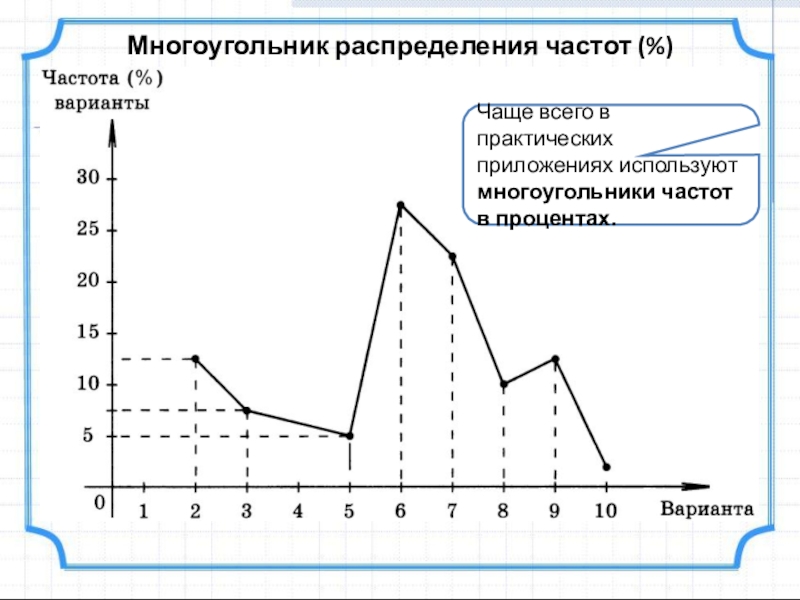
Слайд 12Многоугольник распределения частот (%)
Чаще всего в практических приложениях используют многоугольники частот
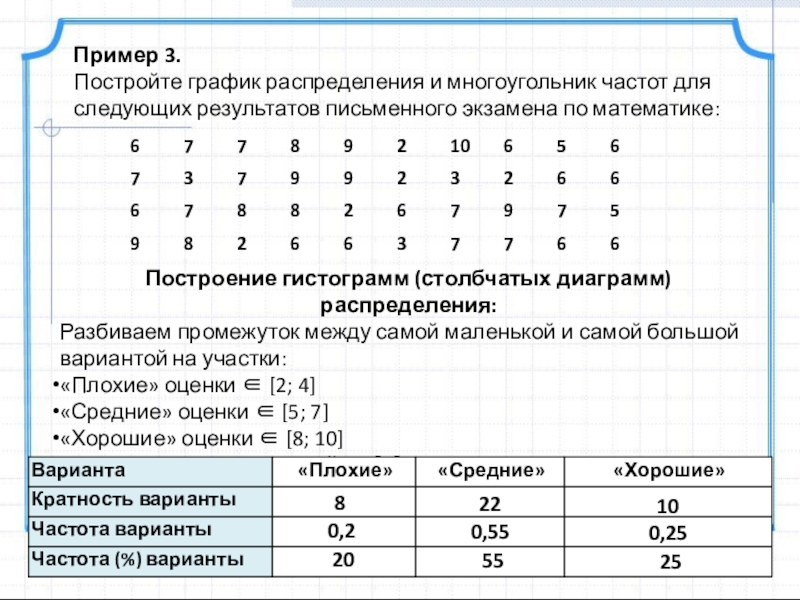
Слайд 13Построение гистограмм (столбчатых диаграмм) распределения:
Разбиваем промежуток между самой маленькой и самой
«Плохие» оценки ∈ [2; 4]
«Средние» оценки ∈ [5; 7]
«Хорошие» оценки ∈ [8; 10]
Получили интервальный ряд данных: 2—4; 5—7; 8—10.
Пример 3.
Постройте график распределения и многоугольник частот для следующих результатов письменного экзамена по математике:
8
22
10
0,2
0,55
0,25
20
55
25
Слайд 17«-» представления информации в виде гистограмм
Теряется первоначальная точная информация
«+»
Ответ получается более
Наглядно видна качественная оценка распределения данных
Слайд 18III. Гистограммы распределения большого объёма информации
Гистограммы незаменимы, когда ряд данных состоит
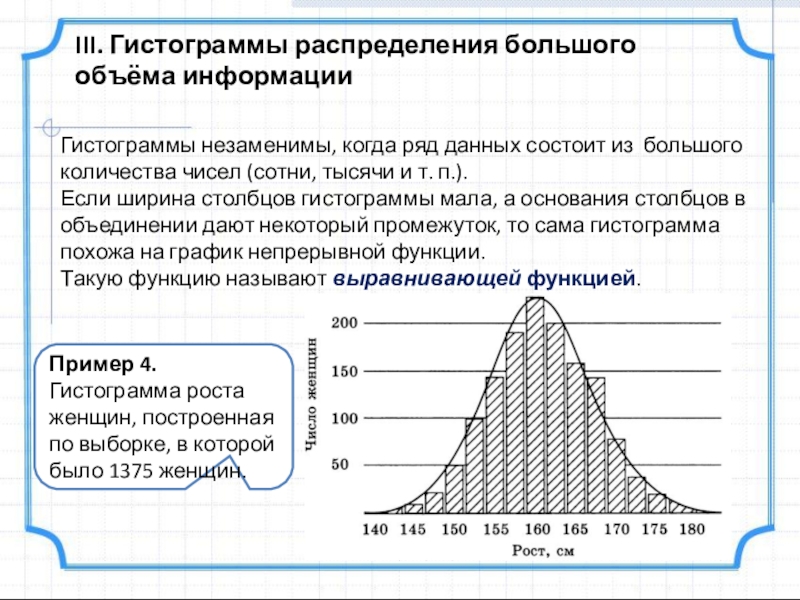
Если ширина столбцов гистограммы мала, а основания столбцов в объединении дают некоторый промежуток, то сама гистограмма похожа на график непрерывной функции.
Такую функцию называют выравнивающей функцией.
Пример 4.
Гистограмма роста женщин, построенная по выборке, в которой было 1375 женщин.
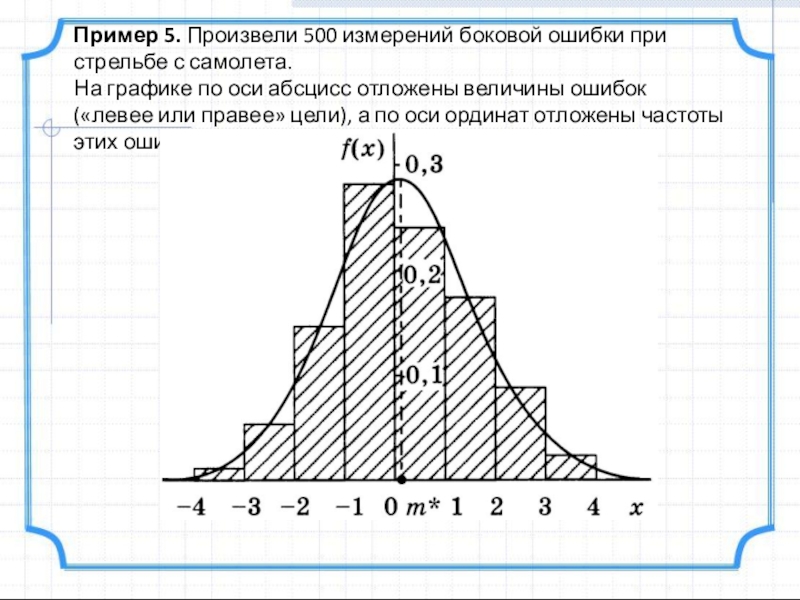
Слайд 19Пример 5. Произвели 500 измерений боковой ошибки при стрельбе с самолета.
На графике по оси абсцисс отложены величины ошибок («левее или правее» цели), а по оси ординат отложены частоты этих ошибок.
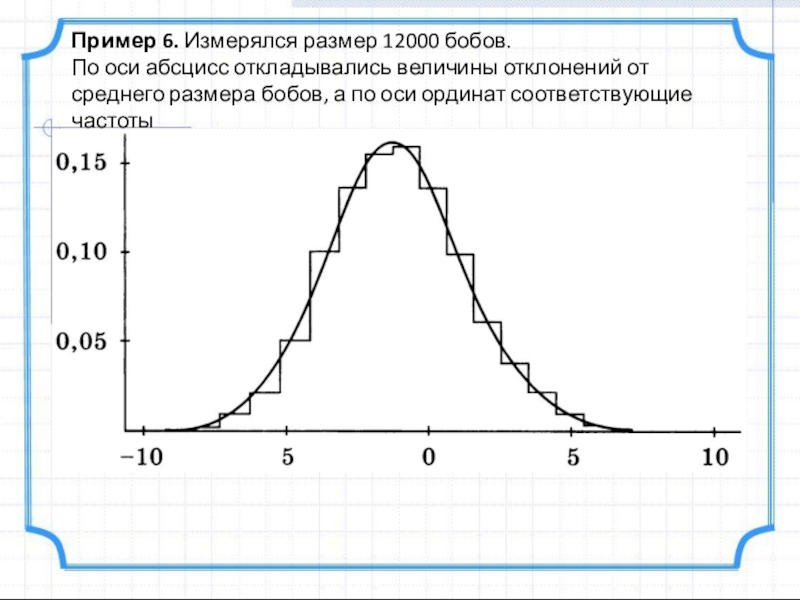
Слайд 20Пример 6. Измерялся размер 12000 бобов.
По оси абсцисс откладывались величины
Слайд 21Примеры взяты из различных областей, а графики функций, выравнивающих гистограммы, похожи
Такому же закону распределения подчиняется:
Распределение горошин по размеру
Распределение новорожденных младенцев по весу
Распределение частиц газа по скоростям движения
…
Все эти кривые получаются из одной кривой.
Её называют кривой нормального распределения или, в честь Карла Гаусса, гауссовой кривой.
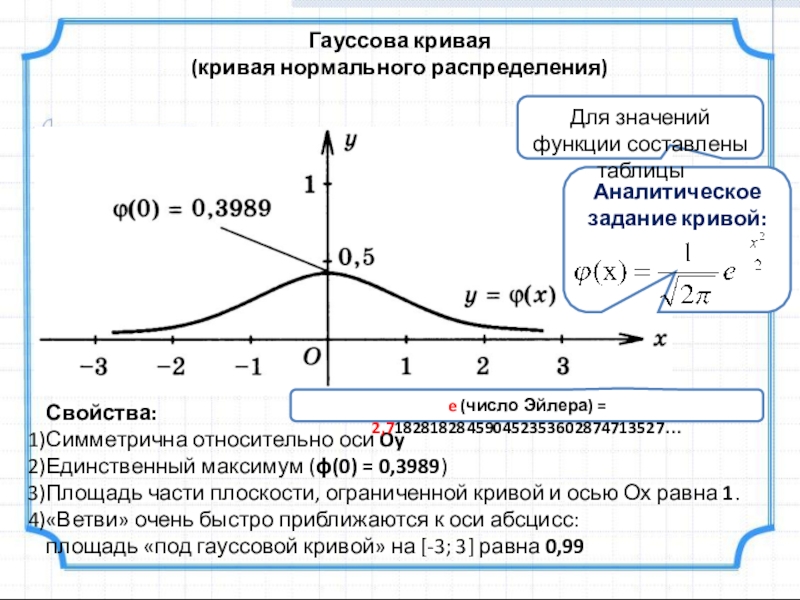
Слайд 22Гауссова кривая
(кривая нормального распределения)
Свойства:
Симметрична относительно оси Oy
Единственный максимум (ϕ(0) = 0,3989)
Площадь
«Ветви» очень быстро приближаются к оси абсцисс: площадь «под гауссовой кривой» на [-3; 3] равна 0,99
Для значений функции составлены таблицы
e (число Эйлера) = 2,7182818284590452353602874713527…
Слайд 23Доска Гальтона (квинкункс, 1873 г.)
Устройство для наглядной демонстрации нормального (гауссова) закона
Принцип действия:
Падающие сверху шарики распределяются между правильными шестиугольниками
В результате попадают на горизонтальную поверхность
Образуют картинку, похожую на «подграфик» гауссовой кривой.
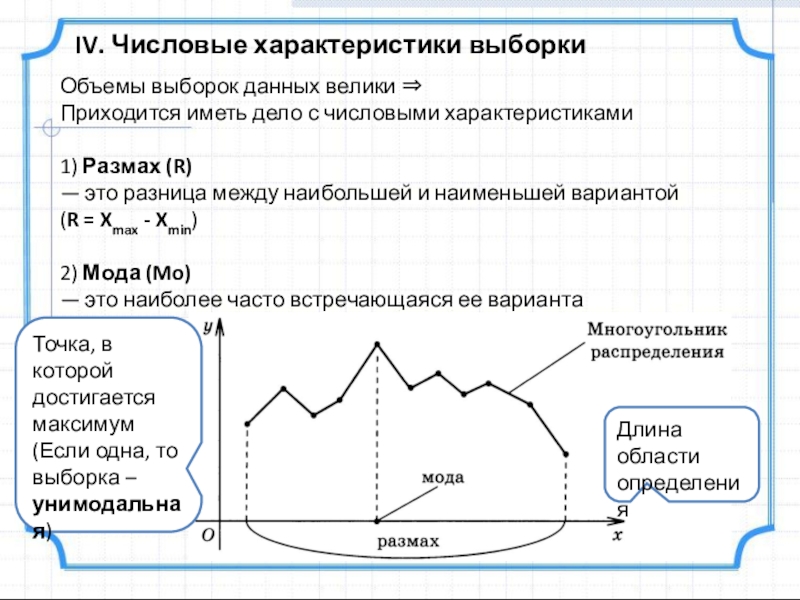
Слайд 24IV. Числовые характеристики выборки
Объемы выборок данных велики ⇒
Приходится иметь дело с
1) Размах (R)
— это разница между наибольшей и наименьшей вариантой
(R = Xmax - Xmin)
2) Мода (Mo)
— это наиболее часто встречающаяся ее варианта
Длина области определения
Точка, в которой достигается максимум
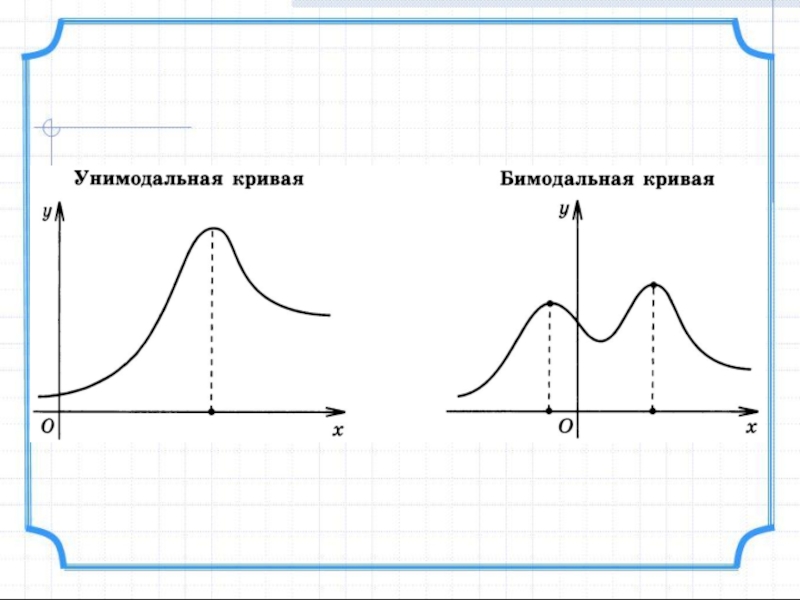
(Если одна, то выборка – унимодальная)
Слайд 263) Медиана (Me)
(от лат. mediana – «среднее»)
Медианой выборки с нечетным числом
Медианой выборки с четным числом вариант называется среднее арифметическое двух вариант, записанных посередине в упорядоченной выборке
Слайд 27Пример 7.
Найдите среднее значение, размах и моду выборки:
а) 32; 26; 18;
1.
2.
Хmax: 32
Хmin: 15
R = Хmax – Хmin = 32 – 15 = 17
3.
Мо = 26
б) 21; 18,5; 25,3; 18,5; 17,9
1.
2.
Xmax: 25,3
Xmin: 17,9
R = Xmax – Xmin = 25,3 – 17,9 = 7,4
3.
Мо = 18,5
Слайд 28Пример 8.
В выборке 2, 7, 10, _, 18, 19, 27 одно
Восстановите его, зная, что среднее значение этих чисел равно 14.
Решение:
Пусть искомое число Х
Ответ: 15
Слайд 29Пример 9.
Найдите медиану выборки:
30, 32, 37, 40, 41, 42, 45, 49,
Пример 10.
Зная, что в упорядоченном ряду содержится m чисел, где m — нечетное число, укажите номер члена, являющегося медианой, если m равно: 5
Решение:
1) Упорядочить выборку: 30, 32, 37, 40, 41, 42, 45, 49, 52
2) Число членов ряда: n = 9
3) Серединный элемент (5-ый): 41
4) Ме = 41
Решение:
Номер члена, являющегося медианой: 3
Слайд 30Пример 11.
В ряду данных, состоящем из 12 чисел, наибольшее число увеличили
а) среднее значение;
б) размах;
в) мода;
г) медиана?
Увеличится на 1/2
Увеличится на 6
Не изменится (?)
Не изменится (?)
Слайд 315) Среднее отклонение ( )
Среднее арифметическое отклонений (в абсолютных
6) Дисперсия (D)
Величина колебания вариант около их среднего значения
7) Среднее квадратичное отклонение (σ - сигма)
8) Коэффициент вариации (CV)
0 ≤ CV ≤ 10% - выборка однородна
11 ≤ CV ≤ 20% - средняя степень однородность
21 ≤ CV – низкая степень однородности
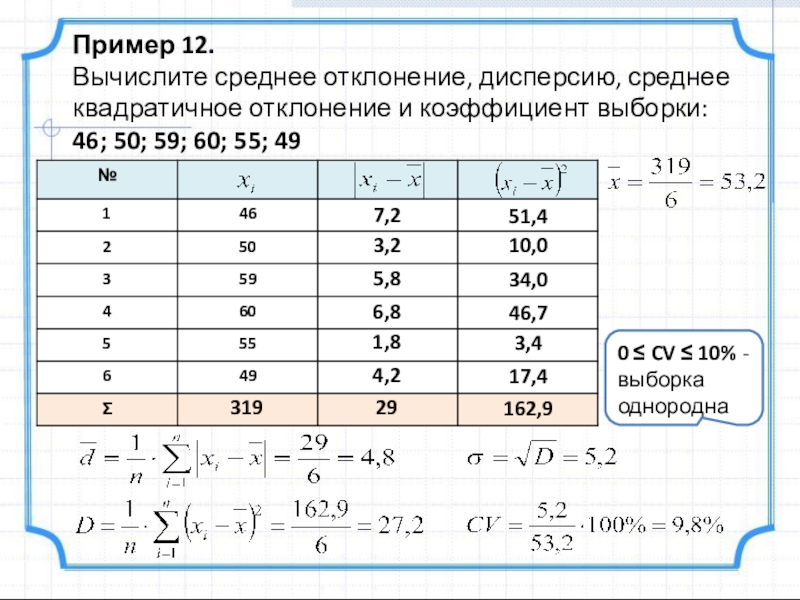
Слайд 32Пример 12.
Вычислите среднее отклонение, дисперсию, среднее квадратичное отклонение и коэффициент выборки:
46;
319
7,2
3,2
5,8
6,8
1,8
4,2
29
51,4
10,0
34,0
46,7
3,4
17,4
162,9
0 ≤ CV ≤ 10% - выборка однородна
Слайд 33V. Экспериментальные данные и вероятности событий
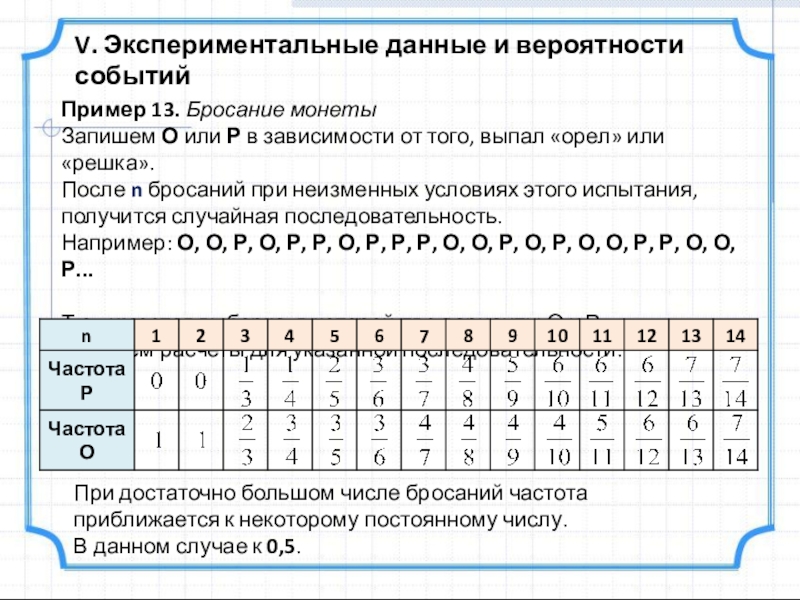
Пример 13. Бросание монеты
Запишем О или
После n бросаний при неизменных условиях этого испытания, получится случайная последовательность.
Например: О, О, Р, О, Р, Р, О, Р, Р, Р, О, О, Р, О, Р, О, О, Р, Р, О, О, Р...
Т.о., имеется выборка, в которой две варианты О и Р.
Сделаем расчеты для указанной последовательности.
При достаточно большом числе бросаний частота приближается к некоторому постоянному числу.
В данном случае к 0,5.
Слайд 34Бросил монету 4040 раз, и при этом герб выпал в 2048
Бросил монету 24000 раз, и при этом герб выпал в 12012 случаях.
Слайд 35Статистическая устойчивость (СУ)
При большом числе независимых повторений одного и того же
СУ имеет место при:
Выпадении определенного числа очков на игральных кубиках
Рождении мальчиков
Времени восхода солнца
…
СУ соединяет реально проводимые испытания с теоретическими моделями этих испытаний.
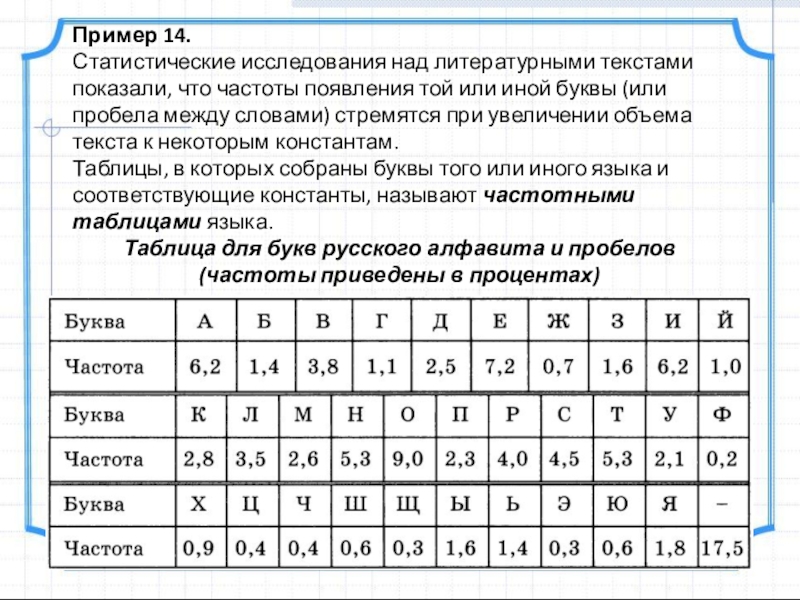
Слайд 36Пример 14.
Статистические исследования над литературными текстами показали, что частоты появления той
Таблицы, в которых собраны буквы того или иного языка и соответствующие константы, называют частотными таблицами языка.
Таблица для букв русского алфавита и пробелов
(частоты приведены в процентах)
Слайд 37Пример 15.
До сегодняшнего дня не утихают споры об авторстве «Тихого Дона».
Многие считают, что в 23 года М. А. Шолохов такую глубокую и поистине великую книгу написать не мог.
Особенно жаркими были споры в момент присуждения М. А. Шолохову Нобелевской премии в области литературы (1965 г.).
Статистический анализ романа и сличение его с текстами, в авторстве которых не было сомнений, подтвердил гипотезу о М. А. Шолохове, как об истинном авторе «Тихого Дона».
М.А. Шолохов
(1905 — 1984)
Слайд 38Пример 16.
В середине 60-х годов в одной из стран Западной Европы
Автором был А. Терц, но это псевдоним.
Был проведен сравнительный анализ опубликованных «вредительских» текстов и результаты были сличены с произведениями ряда возможных кандидатов в авторы.
А.Д. Синявский (1925 — 1997)
Ответ оказался однозначным:
настоящим автором был литературовед А.Д. Синявский.
В 1967 году («Процесс Синявского и Даниэля») получил 5 лет тюрьмы и 7 лет ссылки.



















![Презентация по теме Основы математической статистики Домашнее заданиеМАОУ Лицей ИГУ г. Иркутска, ligu.edu38.ru*КонспектСР «Основы математической статистики»«18_[ДЗ]Основы МС doc» Домашнее заданиеМАОУ Лицей ИГУ г. Иркутска, ligu.edu38.ru*КонспектСР «Основы математической статистики»«18_[ДЗ]Основы МС doc»](/img/thumbs/6faeeed24a375be9f1cb028b779637be-800x.jpg)





