- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по теме: Многогранники
Содержание
- 1. Презентация по теме: Многогранники
- 2. Слайд 2
- 3. Призма
- 4. Опред: Призмой называется многогранник, две грани которого
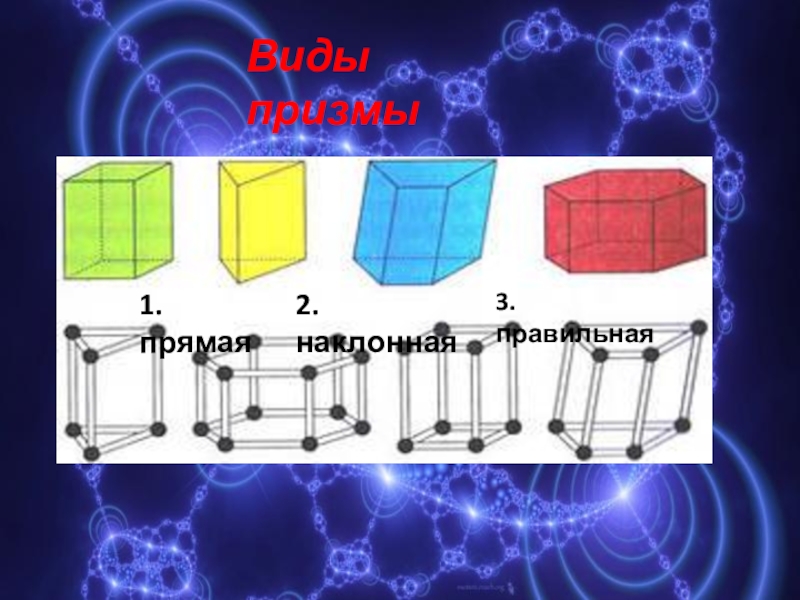
- 5. Виды призмы1.прямая2.наклонная3.правильная
- 6. 1.Прямая призма, если боковые ребра перпендикулярны основаниям2.Наклонная
- 7. Площадь поверхности призмыSполн. пов.= 2S основ. + S бок.пов.
- 8. Теорема1: Площадь боковой поверхности прямой призмы равна
- 9. Пирамида
- 10. Опред: Пирамидой называется многогранник, одна грань которого
- 11. Виды пирамиды1.Правильная пирамида.Правильная - это пирамида, основанием
- 12. Площадь поверхности пирамидыSполн. пов. = S осн.
- 13. Области применения многогранниковФорма снежинок
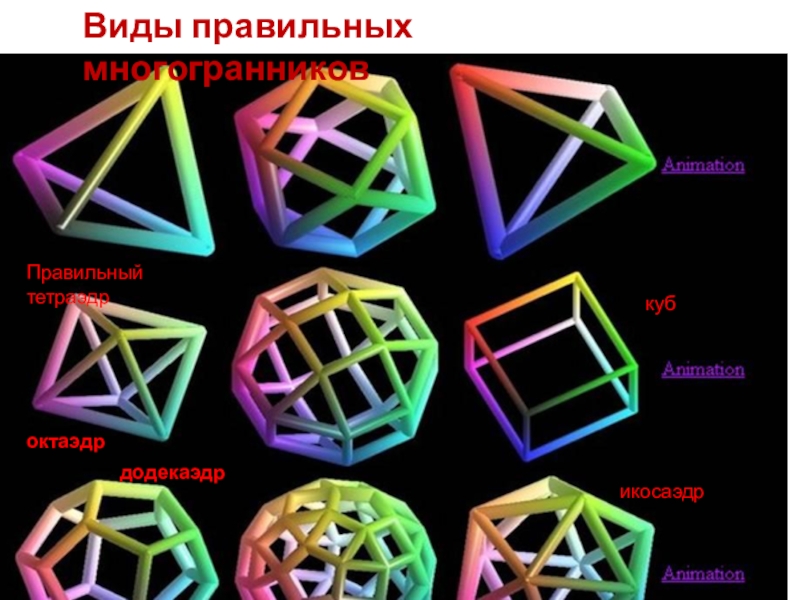
- 14. Виды правильных многогранниковПравильный тетраэдроктаэдрдодекаэдркубикосаэдр
- 15. 1.Правильный тетраэдр- состоит из 4 правильных треугольников2.Октаэдр
- 16. Слайд 16
Слайд 4
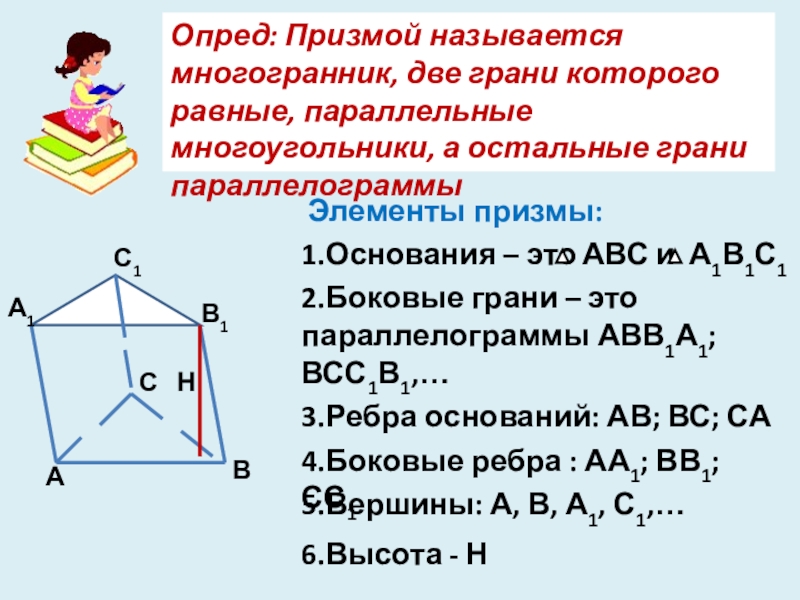
Опред: Призмой называется многогранник, две грани которого равные, параллельные многоугольники, а
А
В
С
А1
В1
С1
Элементы призмы:
1.Основания – это
АВС и
А1В1С1
2.Боковые грани – это параллелограммы АВВ1А1; ВСС1В1,…
3.Ребра оснований: АВ; ВС; СА
4.Боковые ребра : АА1; ВВ1; СС1
5.Вершины: А, В, А1, С1,…
6.Высота - Н
Н
Слайд 61.Прямая призма, если боковые ребра перпендикулярны основаниям
2.Наклонная призма, если боковые ребра
3.Правильная- это прямая призма, основания которой правильные многоугольники
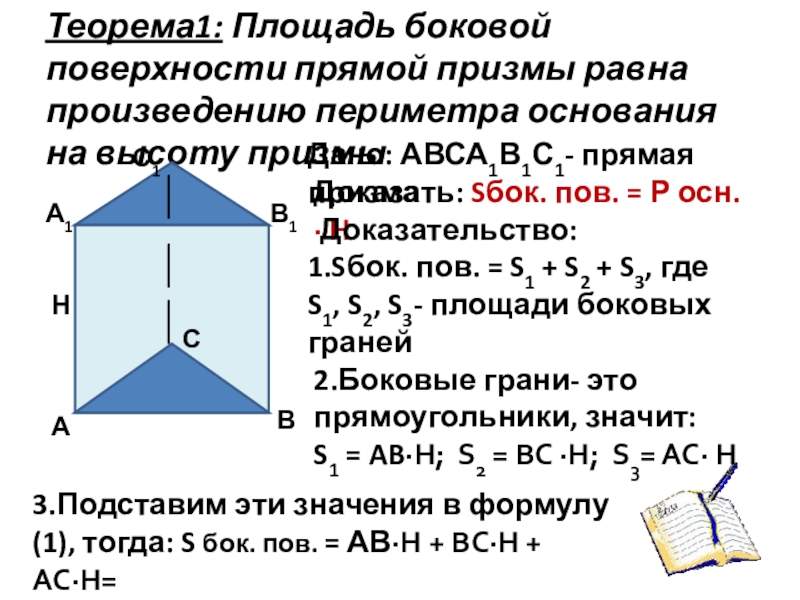
Слайд 8Теорема1: Площадь боковой поверхности прямой призмы равна произведению периметра основания на
А
В
С
А1
В1
С1
Дано: АВСА1В1С1- прямая призма
Доказать: Sбок. пов. = Р осн. ∙ H
Доказательство:
1.Sбок. пов. = S1 + S2 + S3, где
S1, S2, S3- площади боковых граней
2.Боковые грани- это прямоугольники, значит:
S1 = AB∙H; S2 = BC ∙H; S3= AC∙ H
H
3.Подставим эти значения в формулу(1), тогда: S бок. пов. = АВ∙Н + ВС∙Н + АС∙Н=
Н(АВ + ВС + АС) = Н ∙ Р осн.
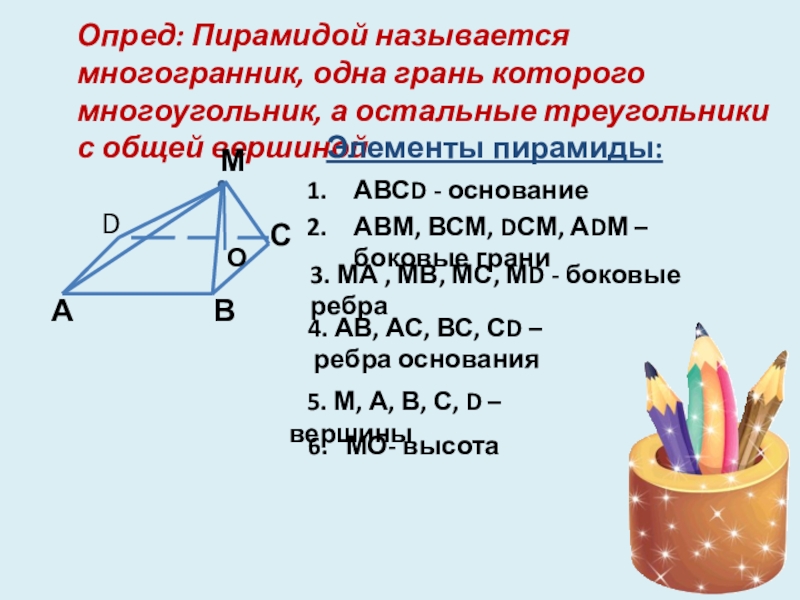
Слайд 10Опред: Пирамидой называется многогранник, одна грань которого многоугольник, а остальные треугольники
А
В
С
D
М
Элементы пирамиды:
АВСD - основание
АВМ, ВСМ, DСМ, АDМ – боковые грани
3. МА , МВ, МС, МD - боковые ребра
4. АВ, АС, ВС, СD –
ребра основания
5. М, А, В, С, D – вершины
6.
МО- высота
О
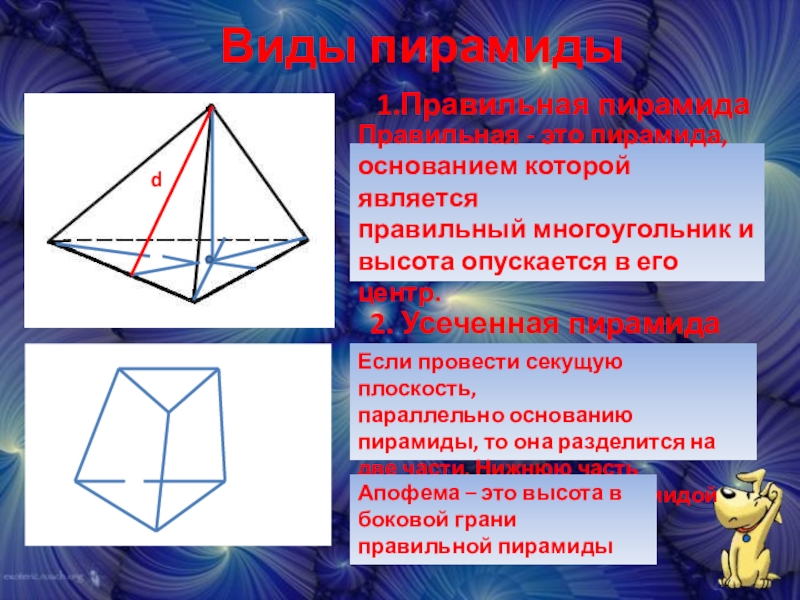
Слайд 11Виды пирамиды
1.Правильная пирамида
.
Правильная - это пирамида,
основанием которой является
правильный многоугольник
высота опускается в его центр.
2. Усеченная пирамида
Если провести секущую плоскость,
параллельно основанию пирамиды, то она разделится на две части. Нижнюю часть называют усеченной пирамидой
d
Апофема – это высота в боковой грани правильной пирамиды
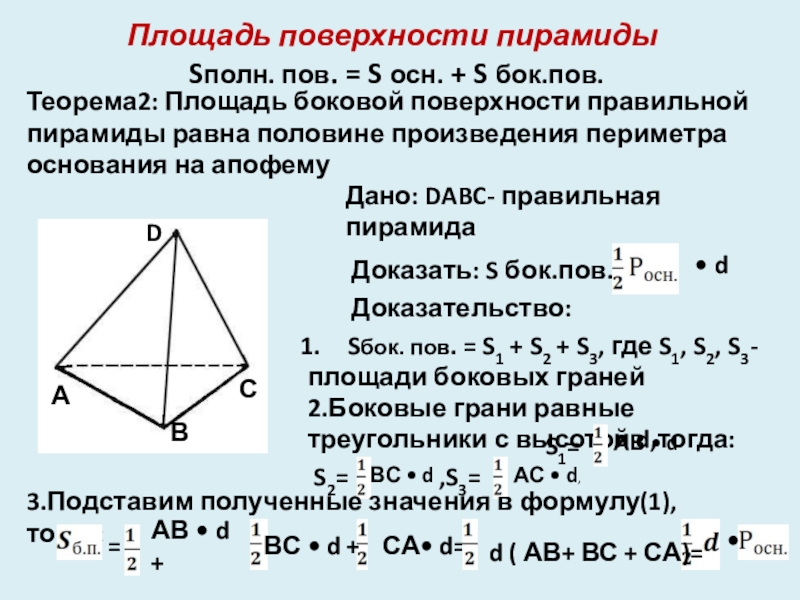
Слайд 12Площадь поверхности пирамиды
Sполн. пов. = S осн. + S бок.пов.
Теорема2:
Дано: DABC- правильная пирамида
А
В
С
D
Доказать: S бок.пов. =
• d
Доказательство:
Sбок. пов. = S1 + S2 + S3, где S1, S2, S3-
площади боковых граней
2.Боковые грани равные треугольники с высотой d,тогда:
S1=
АВ • d
S2=
ВС • d
,S3=
АС • d,
3.Подставим полученные значения в формулу(1), тогда:
=
АВ • d +
ВС • d +
СА• d=
d ( АВ+ ВС + СА)=
•
Слайд 151.Правильный тетраэдр- состоит из 4 правильных треугольников
2.Октаэдр состоит из 8 правильных
3.куб- состоит из 6 квадратов
4.Додекаэдр состоит из 12 правильных пятиугольников
5.Икосаэдр состоит из 20 правильных треугольников