Презентация, доклад по теме Мир фракталов

Содержание

1. Презентация по теме Мир фракталов
2. Мир фракталовМатематика, если на нее правильно посмотреть, отражает не только истину, но и несравненную красоту.Бертранд Рассел
3. Мир фракталовМИР ФРАКТАЛОВ
4. Роль фракталов в современном мире достаточно велика.
5. создание фрактальных изображений в
6. Мир фракталовГеорг Кантор, 3 марта 1845 г.
7. Мир фракталовТермин «фрактал» был введён Бенуа Мандельбротом в 1975 году и получил
8. Мир фракталовФракталами называют бесконечно самоподобные фигуры, каждый
9. Классификация фракталов:геометрические фракталыалгебраические фракталы- стохастические фракталы
10. Геометрические фракталы
11. Нильс Фабиан Хельге фон Кох (25 января 1870 — 11 марта 1924) — шведский математик
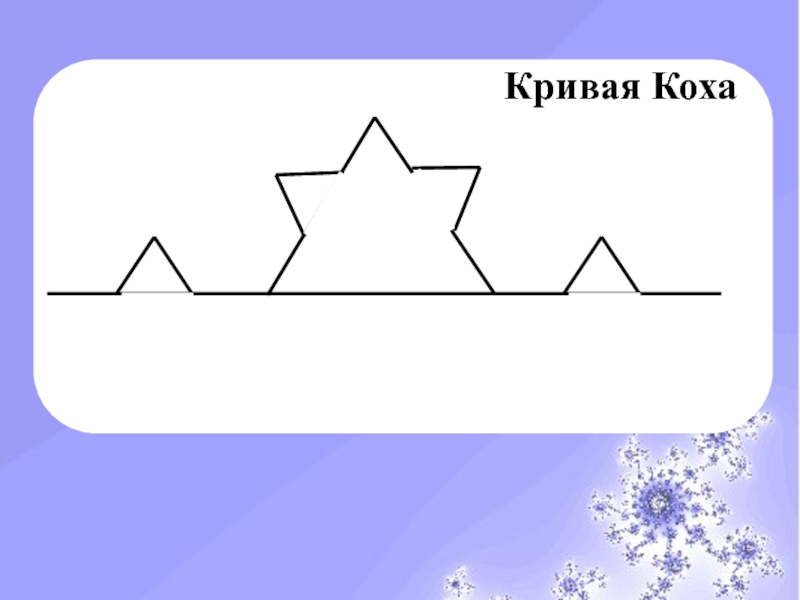
12. Кривая Коха
13. Мир фракталовКривая Коха
14. Мир фракталов
15. Мир фракталовСнежинка Коха образуется из трех соединенных вместе кривых Коха.
16. Мир фракталовСнежинка Коха «наоборот» получается, если строить кривые Коха внутрь исходного равностороннего треугольника.
17. Мир фракталовТрехмерные аналоги. Пирамида Коха.
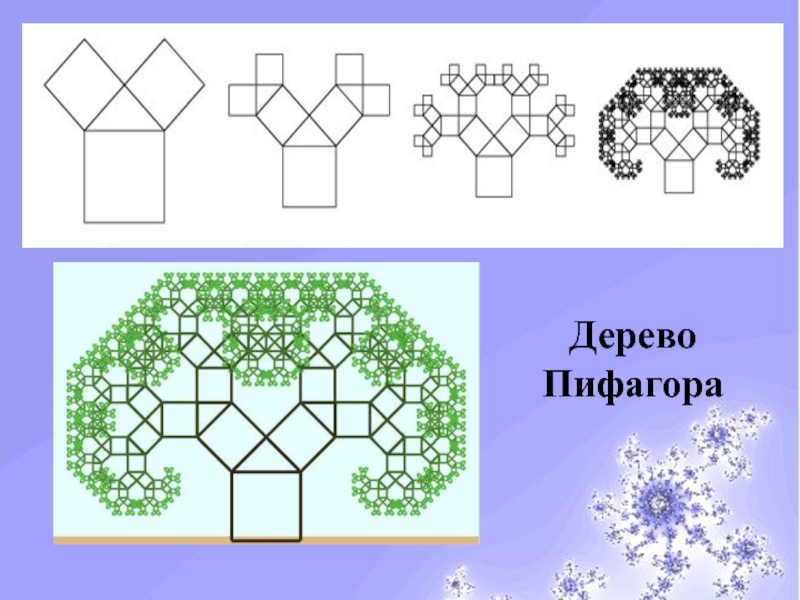
18. Мир фракталовДерево Пифагора
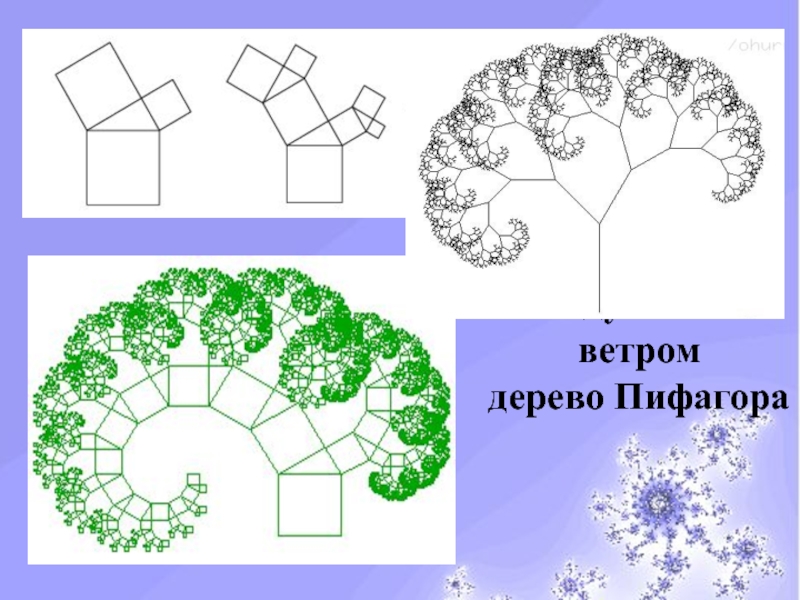
19. Мир фракталовОбдуваемое ветром дерево Пифагора
20. Мир фракталовДерево Пифагора
21. Мир фракталовТреугольник Серпинского
22. Мир фракталовТреугольник Серпинского
23. Мир фракталовКривая дракона
24. Мир фракталов Алгебраические фракталы
25. Мир фракталовФрактал МандельбротаФрактал Мандельброта
26. Мир фракталовФрактал Ньютона
27. Мир фракталовМножества Жюлиа
28. Мир фракталов Стохастические фракталы
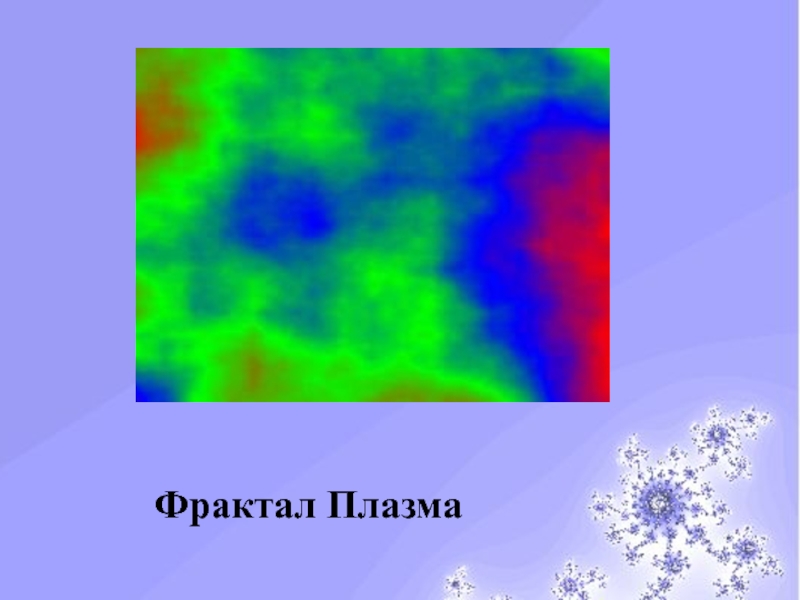
29. Мир фракталовФрактал Плазма
30. Мир фракталов Фрактальная геометрия природы
31. Мир фракталовВ природе
32. Мир фракталовВ природе
33. Мир фракталовВ природе
34. Мир фракталовВ природе
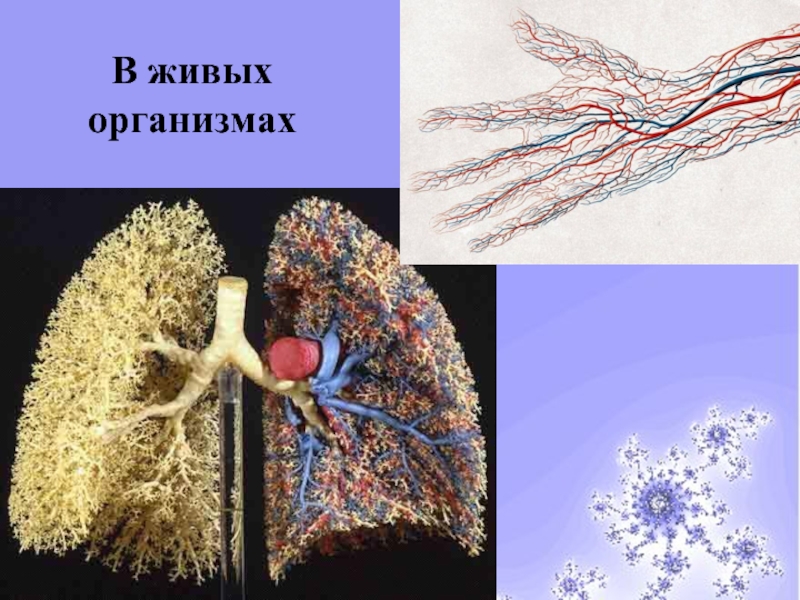
35. Мир фракталовВ живых организмах
36. Мир фракталовВ рельефе земли
37. Мир фракталов Практическая работа
38. Геометрический фрактал, созданный мной :
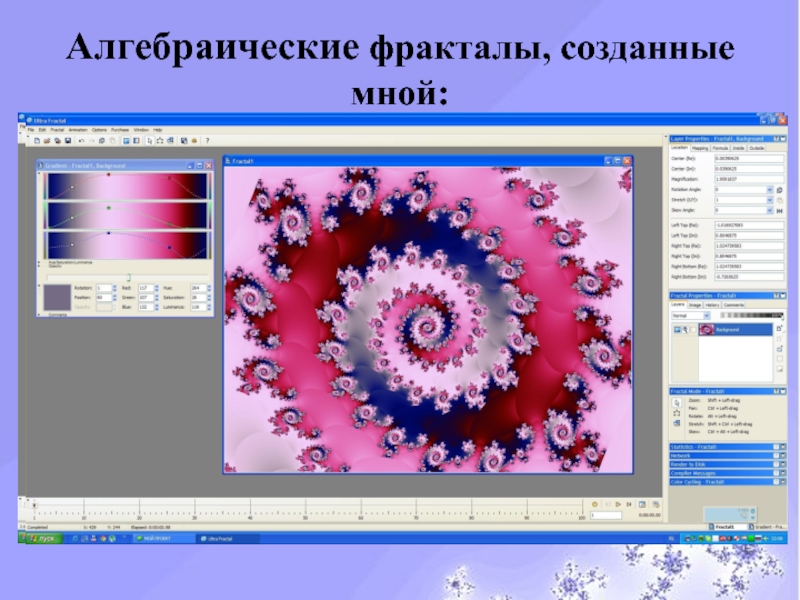
39. Алгебраические фракталы, созданные мной:
40. Мир фракталов Красота фракталов
41. Мир фракталов
42. Мир фракталов
43. Мир фракталов
44. Мир фракталов
45. Мир фракталов
46. Мир фракталов
47. Мир фракталов
48. Мир фракталовМатематика вся пронизана красотой и гармонией,

Мир фракталовМатематика, если на нее правильно посмотреть, отражает не только истину, но и несравненную красоту.Бертранд Рассел

Главная
Математика
Презентация по теме Мир фракталов

Слайд 1Мир фракталов
ЭСТЕТИКА ГЕОМЕТРИЧЕСКИХ ФОРМ
Работу выполнил: Ловаков Кирилл,

обучающийся 11 класса
Руководитель: О. А. Оксененко

Слайд 2Мир фракталов
Математика, если на нее правильно посмотреть, отражает не только истину,

но и несравненную красоту.
Бертранд Рассел

Слайд 3Мир фракталов
МИР ФРАКТАЛОВ

Слайд 4Роль фракталов в современном мире достаточно велика. Они постоянно приходят на

помощь ученым, инженерам, дизайнерам, компьютерщикам.

Одним из самых убедительных аргументов в пользу актуальности фракталов является широта их области применения.
Компьютерные системы (фрактальное сжатие данных).
Децентрализованные сети (принцип фрактального сжатия информации гарантирует полностью децентрализованную, а, следовательно, максимально устойчивую работу всей сети).
Радиотехника (фрактальные антенны).
В естественных науках (физика, биология, телекоммуникации, медицина).
Экономика и финансы (использование фракталов при анализе биржевых котировок).
Компьютерная графика (построение изображений природных объектов).

Актуальность.

Роль фракталов в современном мире достаточно велика. Они постоянно приходят на помощь ученым, инженерам, дизайнерам, компьютерщикам. Одним из

Слайд 5 создание фрактальных изображений в программах Adobe Photoshop CS5

и Ultra Fractal 5.0.
Задачи:
знакомство с понятием, историей возникновения и исследованиями Б.Мандельброта, Г. Коха, В. Серпинского и др.;
знакомство с различными видами классификаций фрактальных множеств;
нахождение подтверждения теории фрактальности окружающего мира;
изучение применения темы в других науках и на практике;
проведение эксперимента по созданию собственного фрактального изображения.

Цель работы: