- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по теме Метод раскраски.
Содержание
- 1. Презентация по теме Метод раскраски.
- 2. ШАХМАТНАЯ РАСКРАСКА
- 3. Задача 1. Из обычной шахматной доски 8х8
- 4. Задача 2. Из обычной шахматной доски 8х8
- 5. Задача 2. Из обычной шахматной доски 8х8
- 6. Задача 3. Из обычной шахматной доски 8х8
- 7. Задача 4. Докажите, что если из шахматной
- 8. Задача 4. Докажите, что если из шахматной
- 9. Задача 5. (ТГ, 12, 1990/91, осенний тур,
- 10. Задача 5. (ТГ, 12, 1990/91, осенний тур,
- 11. Задача 6. В каждой клетке доски 5×5 клеток
- 12. Задача 6. В каждой клетке доски 5×5 клеток
- 13. Задача 7. На каждой из клеток размером
- 14. Задача 8. (Автор: Ботинн М.А., Математический праздник
- 15. Задача 8. (Автор: Ботинн М.А., Математический праздник
- 16. Задача 9. Кусок сыра имеет форму кубика
- 17. Задача 10. Деревянный брусок тремя распилами распилили
- 18. Задача 10. Деревянный брусок тремя распилами распилили
- 19. Задача 11. Каждая сторона равностороннего треугольника разбита
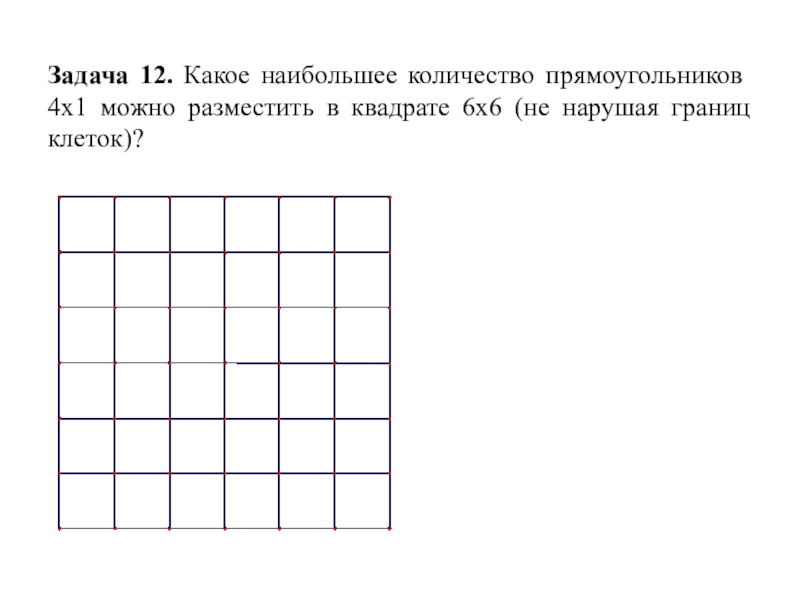
- 20. Задача 12. Какое наибольшее количество прямоугольников 4х1 можно разместить в квадрате 6х6 (не нарушая границ клеток)?
- 21. Задача 12. Какое наибольшее количество прямоугольников 4х1 можно разместить в квадрате 6х6 (не нарушая границ клеток)?
- 22. Задача 12. Какое наибольшее количество прямоугольников 4х1 можно разместить в квадрате 6х6 (не нарушая границ клеток)?
- 23. Задача 12. Какое наибольшее количество прямоугольников 4х1 можно разместить в квадрате 6х6 (не нарушая границ клеток)?
- 24. ВСПОМОГАТЕЛЬНАЯ РАСКРАСКА
- 25. ПОПУЛЯРНЫЕ РАСКРАСКИ
- 26. ПОПУЛЯРНЫЕ РАСКРАСКИ
- 27. ПОПУЛЯРНЫЕ РАСКРАСКИ
- 28. ПОПУЛЯРНЫЕ РАСКРАСКИ
- 29. ПОПУЛЯРНЫЕ РАСКРАСКИ
- 30. Задача 12. Какое наибольшее количество прямоугольников 4х1 можно разместить в квадрате 6х6 (не нарушая границ клеток)?
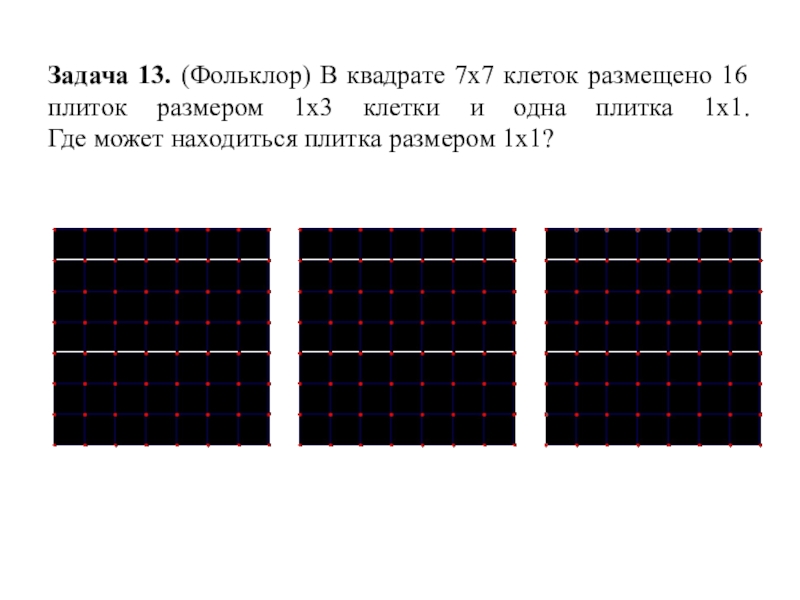
- 31. Задача 13. (Фольклор) В квадрате 7х7 клеток
- 32. Задача 14. (Фольклор) Дно прямоугольной коробки выложено
- 33. Задача 15. (Автор: Фомин С.В.) ТГ1983/1984 ,
- 34. Задача 16. (Автор: Скопенков А.Б., Всероссийская олимпиада
- 35. ИСПОЛЬЗУЕМАЯ ЛИТЕРАТУРА:Прасолов, Задачи по планиметрии1000 задач ТГГорбачевСборники задач Всероссийских олимпиад Сайт www.problems.ruЧертежи выполнены в программе«Живая геометрия»
- 36. СПАСИБОЗА ВНИМАНИЕ!!!Мой e-mail: vladimir_zhuk@mail.ru
ШАХМАТНАЯ РАСКРАСКА
Слайд 1Метод раскраски
Жук Владимир Васильевич,
к.ф.-м.н.,учитель математики
РСФМСШИ им. О. Жаутыкова
vladimir_zhuk@mail.ru
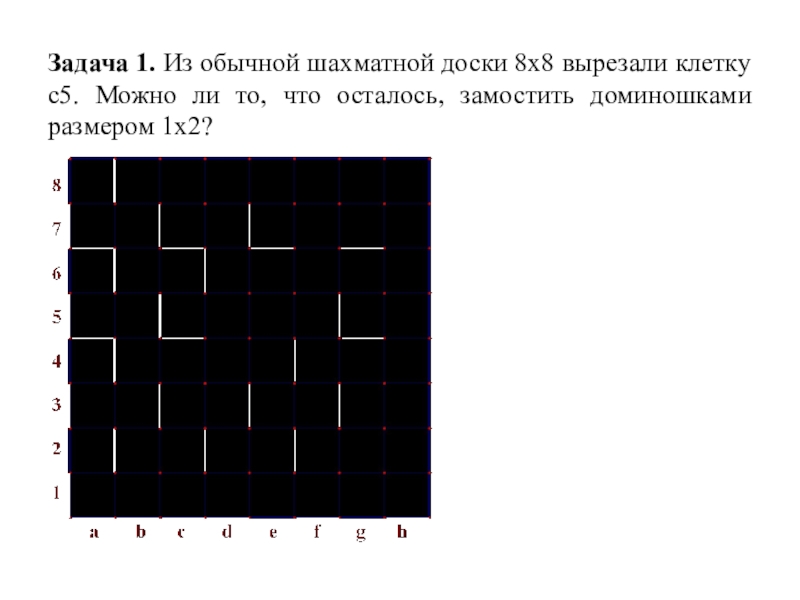
Слайд 3Задача 1. Из обычной шахматной доски 8х8 вырезали клетку с5. Можно
ли то, что осталось, замостить доминошками размером 1х2?
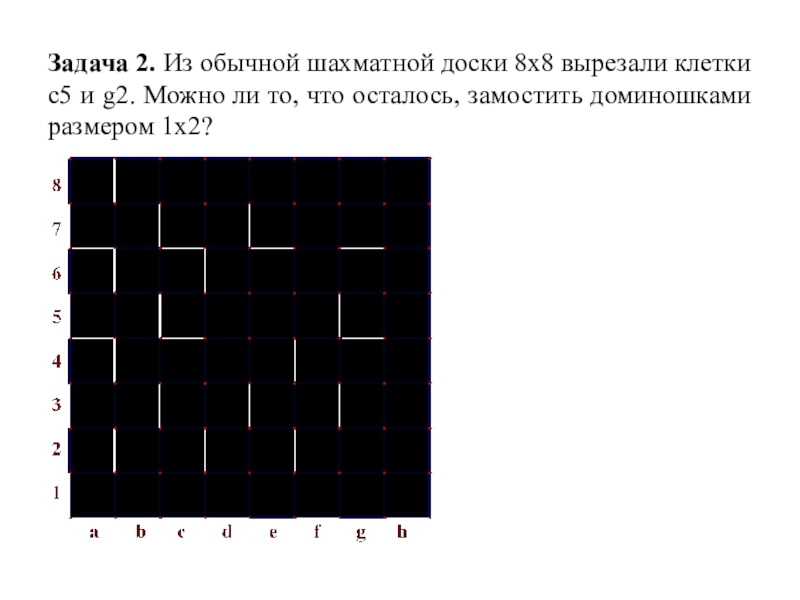
Слайд 4Задача 2. Из обычной шахматной доски 8х8 вырезали клетки с5 и
g2. Можно ли то, что осталось, замостить доминошками размером 1х2?
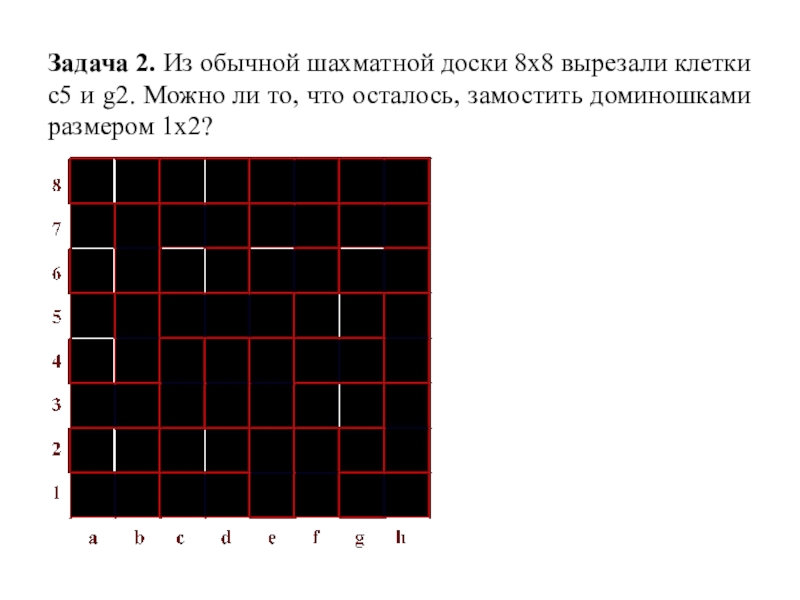
Слайд 5Задача 2. Из обычной шахматной доски 8х8 вырезали клетки с5 и
g2. Можно ли то, что осталось, замостить доминошками размером 1х2?
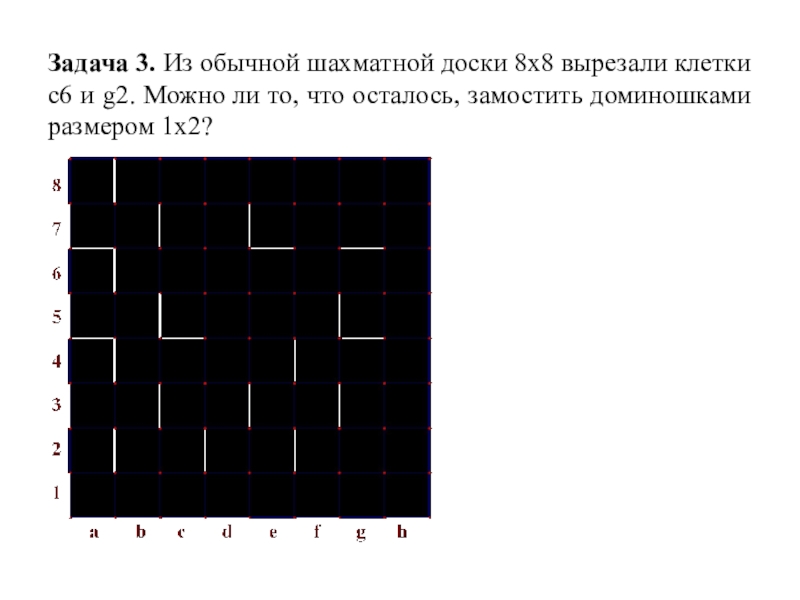
Слайд 6Задача 3. Из обычной шахматной доски 8х8 вырезали клетки с6 и
g2. Можно ли то, что осталось, замостить доминошками размером 1х2?
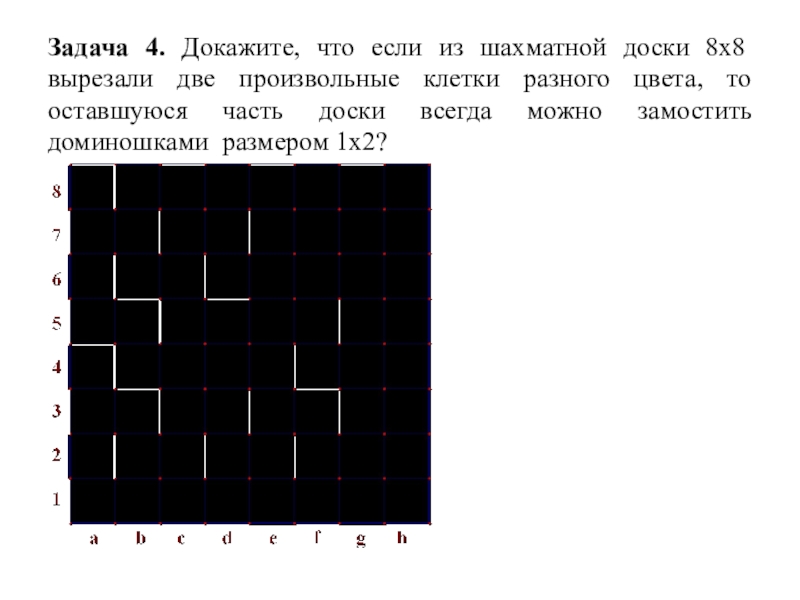
Слайд 7Задача 4. Докажите, что если из шахматной доски 8х8 вырезали две
произвольные клетки разного цвета, то оставшуюся часть доски всегда можно замостить доминошками размером 1х2?
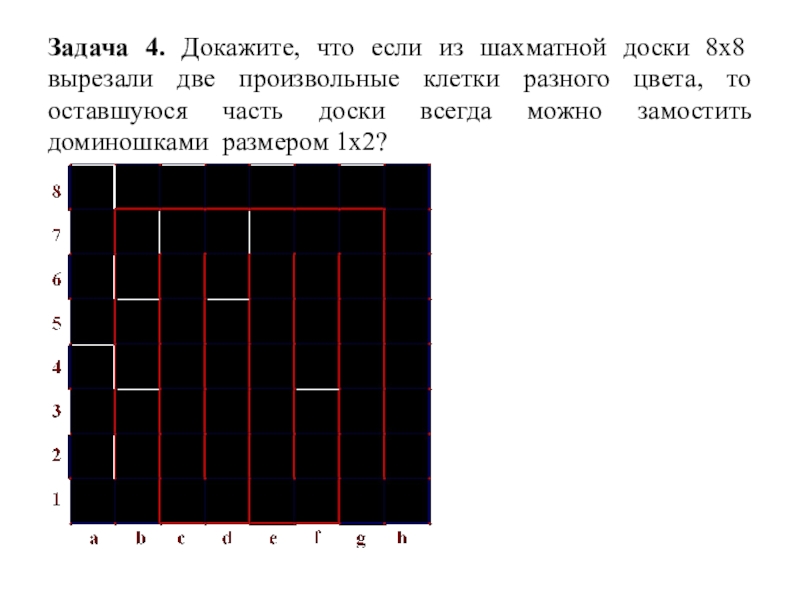
Слайд 8Задача 4. Докажите, что если из шахматной доски 8х8 вырезали две
произвольные клетки разного цвета, то оставшуюся часть доски всегда можно замостить доминошками размером 1х2?
Слайд 9Задача 5. (ТГ, 12, 1990/91, осенний тур, тренировочный вариант, 8-9 класс,
4 задача) Доска 100 на 100 разбита на 10000 единичных квадратиков. Один из них вырезали, так что образовалась дырка. Можно ли оставшуюся часть доски покрыть равнобедренными прямоугольными треугольниками с гипотенузой длины 2 так, чтобы их гипотенузы шли по сторонам квадратиков, а катеты - по диагоналям и чтобы треугольники не налегали друг на друга и не свисали с доски?
Слайд 10Задача 5. (ТГ, 12, 1990/91, осенний тур, тренировочный вариант, 8-9 класс,
4 задача) Доска 100 на 100 разбита на 10000 единичных квадратиков. Один из них вырезали, так что образовалась дырка. Можно ли оставшуюся часть доски покрыть равнобедренными прямоугольными треугольниками с гипотенузой длины 2 так, чтобы их гипотенузы шли по сторонам квадратиков, а катеты - по диагоналям и чтобы треугольники не налегали друг на друга и не свисали с доски?
Слайд 11Задача 6. В каждой клетке доски 5×5 клеток сидит жук. В некоторый момент
все жуки переползают на соседние (по горизонтали или вертикали) клетки. Обязательно ли при этом останется пустая клетка?
Слайд 12Задача 6. В каждой клетке доски 5×5 клеток сидит жук. В некоторый момент
все жуки переползают на соседние (по горизонтали или вертикали) клетки. Обязательно ли при этом останется пустая клетка?
Слайд 13Задача 7. На каждой из клеток размером 9х9 находится фишка. Петя
хочет передвинуть каждую фишку на соседнюю по стороне клетку так, чтобы снова в каждой из клеток оказалось по одной фишке. Сможет ли Петя это сделать?
Слайд 14Задача 8. (Автор: Ботинн М.А., Математический праздник 1990 г.. 6,7 классы,
задача №3) Можно ли из 13 кирпичей 1×1×2 сложить куб 3×3×3 с дыркой 1×1×1 в центре?
Слайд 15Задача 8. (Автор: Ботинн М.А., Математический праздник 1990 г.. 6,7 классы,
задача №3) Можно ли из 13 кирпичей 1×1×2 сложить куб 3×3×3 с дыркой 1×1×1 в центре?
Слайд 16Задача 9. Кусок сыра имеет форму кубика 3×3×3, из которого вырезан
центральный кубик. Мышь начинает грызть этот кусок сыра. Сначала она съедает некоторый кубик 1×1×1. После того, как мышь съедает очередной кубик 1×1×1, она приступает к съедению одного из соседних (по грани) кубиков с только что съеденным. Сможет ли мышь съесть весь кусок сыра?
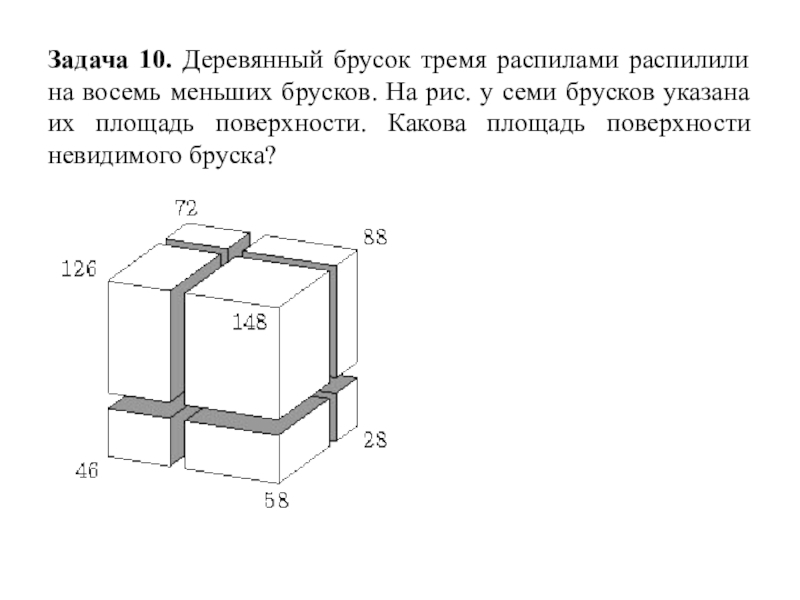
Слайд 17Задача 10. Деревянный брусок тремя распилами распилили на восемь меньших брусков.
На рис. у семи брусков указана их площадь поверхности. Какова площадь поверхности невидимого бруска?
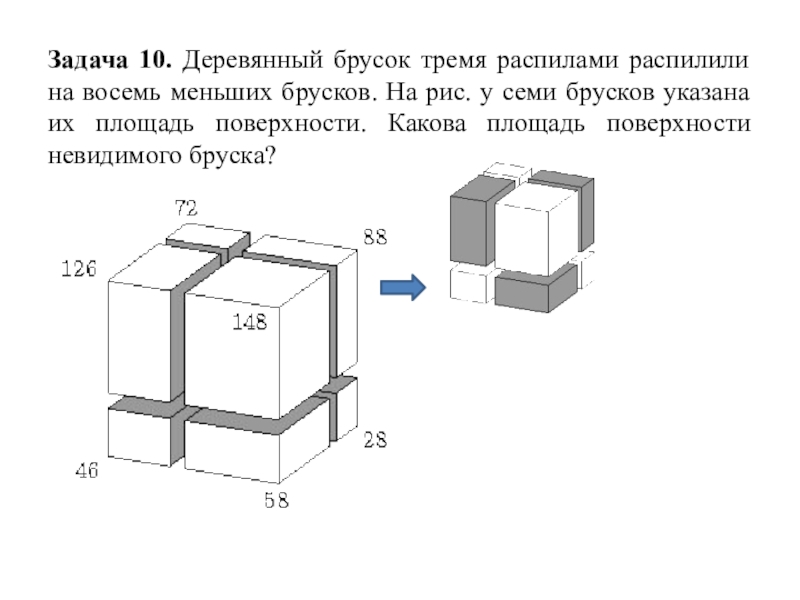
Слайд 18Задача 10. Деревянный брусок тремя распилами распилили на восемь меньших брусков.
На рис. у семи брусков указана их площадь поверхности. Какова площадь поверхности невидимого бруска?
Слайд 19Задача 11. Каждая сторона равностороннего треугольника разбита на n равных частей.
Через точки деления проведены прямые, параллельные сторонам. В результате треугольник разбит на n2 треугольничков. Назовём цепочкой последовательность треугольничков, в которой ни один не появляется дважды и каждый последующий имеет общую сторону с предыдущим. Каково наибольшее возможное количество треугольничков в цепочке?
Слайд 20Задача 12. Какое наибольшее количество прямоугольников 4х1 можно разместить в квадрате
6х6 (не нарушая границ клеток)?
Слайд 21Задача 12. Какое наибольшее количество прямоугольников 4х1 можно разместить в квадрате
6х6 (не нарушая границ клеток)?
Слайд 22Задача 12. Какое наибольшее количество прямоугольников 4х1 можно разместить в квадрате
6х6 (не нарушая границ клеток)?
Слайд 23Задача 12. Какое наибольшее количество прямоугольников 4х1 можно разместить в квадрате
6х6 (не нарушая границ клеток)?
Слайд 30Задача 12. Какое наибольшее количество прямоугольников 4х1 можно разместить в квадрате
6х6 (не нарушая границ клеток)?
Слайд 31Задача 13. (Фольклор) В квадрате 7х7 клеток размещено 16 плиток размером
1х3 клетки и одна плитка 1х1.
Где может находиться плитка размером 1х1?
Слайд 32Задача 14. (Фольклор) Дно прямоугольной коробки выложено плитками размером 2×2 и 1×4.
Плитки высыпали из коробки и потеряли одну плитку 2×2. Вместо нее достали плитку 1×4. Докажите, что выложить дно коробки плитками теперь не удастся.
Слайд 33Задача 15. (Автор: Фомин С.В.) ТГ1983/1984 , 5 весенний тур, подготовительный
вариант, 9-10 класс, задача 3) Из листа клетчатой бумаги размером 29х29 клеточек вырезали 99 квадратиков 2х2 (режут по линиям). Доказать, что из оставшейся части листа можно вырезать ещё хотя бы один такой же квадратик.
Слайд 34Задача 16. (Автор: Скопенков А.Б., Всероссийская олимпиада по математике, 1997 г.,
4 этап, 11 класс, задача 4) Дан куб со стороной 4. Можно ли целиком оклеить 3 его грани, имеющие общую вершину, шестнадцатью бумажными прямоугольными полосками размером 1×3?
Слайд 35ИСПОЛЬЗУЕМАЯ ЛИТЕРАТУРА:
Прасолов, Задачи по планиметрии
1000 задач ТГ
Горбачев
Сборники задач Всероссийских олимпиад
Сайт
www.problems.ru
Чертежи выполнены в программе
«Живая геометрия»
Чертежи выполнены в программе
«Живая геометрия»