- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
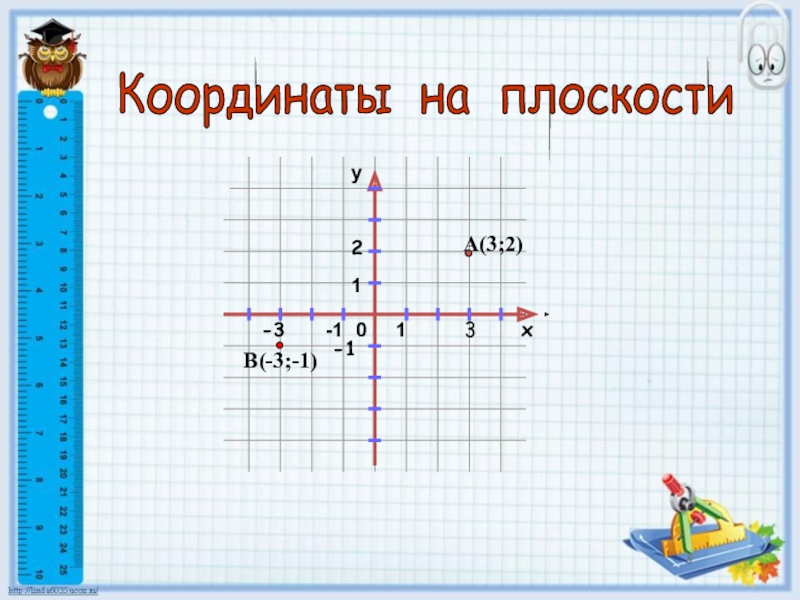
Презентация, доклад по теме: Координаты на плоскости
Содержание
- 1. Презентация по теме: Координаты на плоскости
- 2. Система координат – это правило, по которому
- 3. Линия времени
- 4. Более чем за 100 лет до н.э
- 5. Во II веке н.э. знаменитый древнегреческий астроном
- 6. Рене Декарт (1596-1650) французский философ, естествоиспытатель, математик.
- 7. Для этого введем на плоскости систему координат.
- 8. xКаждой точке на координатной плоскости, соответствует пара
- 9. Плоскость, на которой задана система координат, называется
- 10. 11оухСистема координатСистема координат, с которой мы только
- 11. y х о 1 2 3 4
- 12. АGСF1DЕВК(-3; 0)(0; 3)(3; 0)(0;-3)P(0; 2)(-2; 0)(0;-2)(2; 0)O(-2;
- 13. ХУ01(1;7)(2;0)(-5;4)(0;-3)(7;-5)(-7;0)(-6;-4)(0;1)(0;5)(3;-4)(0:-8)(5;3)(-4;0)(-3;-5)(9;0)(-2;9)1-1-123946-578-232456789-3-45-6-7-3-2-4-6-5-7-8Отметь точку на координатной плоскости.Наведи курсор на
- 14. Определи в какой четверти находится точка.( 5;
- 15. (-2;0) (-2;12) (2;6) Точки: (0;2)
- 16. Итог урока Выберите
Слайд 2Система координат – это правило, по которому определяется положение того или
Примеры систем координат,
встречающихся в жизни
Номер ряда и
места в театре
Широта и долгота местности на географической карте
Номер дома, квартиры
адресата
ШАХМАТЫ
Слайд 4Более чем за 100 лет до н.э греческий ученый Гиппарх предложил
Греческое изображение глобуса 150 г. н. э
Слайд 5Во II веке н.э. знаменитый древнегреческий астроном Клавдий Птолемей уже пользовался
Карта Птолемея
Слайд 6Рене Декарт (1596-1650) французский философ, естествоиспытатель, математик. Он ввёл метод координат,
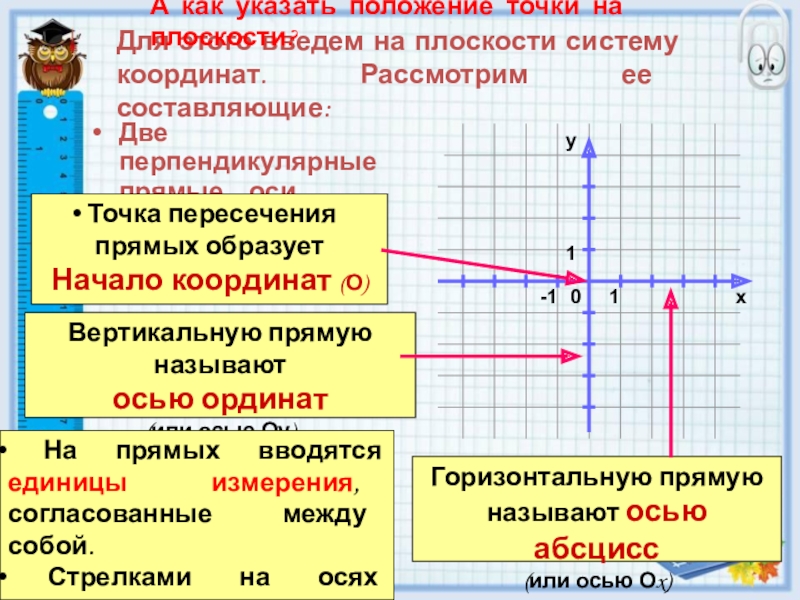
Слайд 7Для этого введем на плоскости систему координат. Рассмотрим ее составляющие:
Две перпендикулярные прямые – оси координат
0
x
y
1
1
-1
Горизонтальную прямую называют осью абсцисс
(или осью Оx)
Вертикальную прямую называют
осью ординат
(или осью Оу)
А как указать положение точки на плоскости?
Точка пересечения прямых образует
Начало координат (О)
На прямых вводятся единицы измерения, согласованные между собой.
Стрелками на осях указывается положительное направление.
Слайд 8x
Каждой точке на координатной плоскости, соответствует пара чисел: ее абсцисса (х)
Чтобы найти координаты точки А, необходимо через нее провести прямые, перпендикулярные осям координат.
Координаты точки записывают в скобках через точку с запятой, причем первой всегда записывается координата х, второй координата у.
Точка А имеет координаты:
по оси абсцисс – 3,
по оси ординат – 2.
Записывают так: А(3;2).
Аналогично найдем координаты точек В и С:
мы получаем: В(-3;-1), С(2;-4).
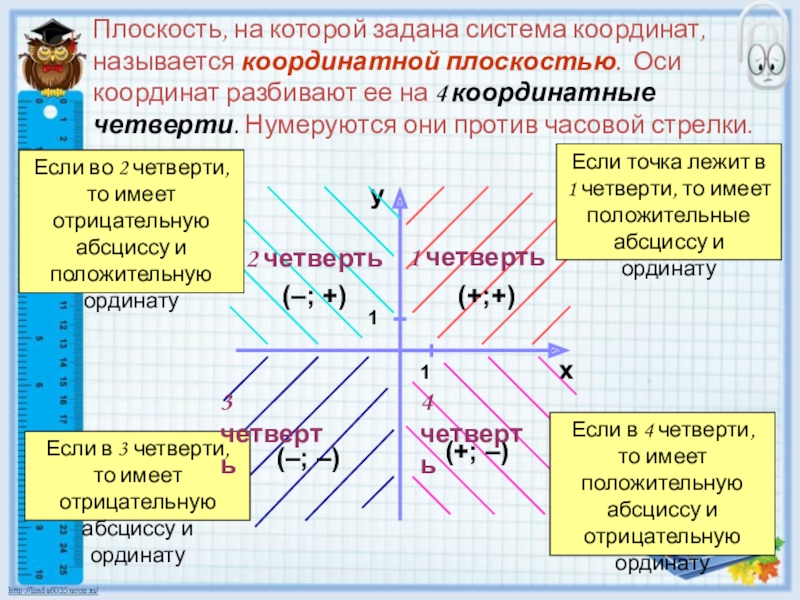
Слайд 9Плоскость, на которой задана система координат, называется координатной плоскостью. Оси координат
1
1
x
y
Если точка лежит в 1 четверти, то имеет положительные абсциссу и ординату
(+;+)
Если во 2 четверти, то имеет отрицательную абсциссу и положительную ординату
(–; +)
Если в 3 четверти, то имеет отрицательную абсциссу и ординату
(–; –)
Если в 4 четверти, то имеет положительную абсциссу и отрицательную ординату
(+; –)
1 четверть
2 четверть
4 четверть
3 четверть
Слайд 101
1
о
у
х
Система
координат
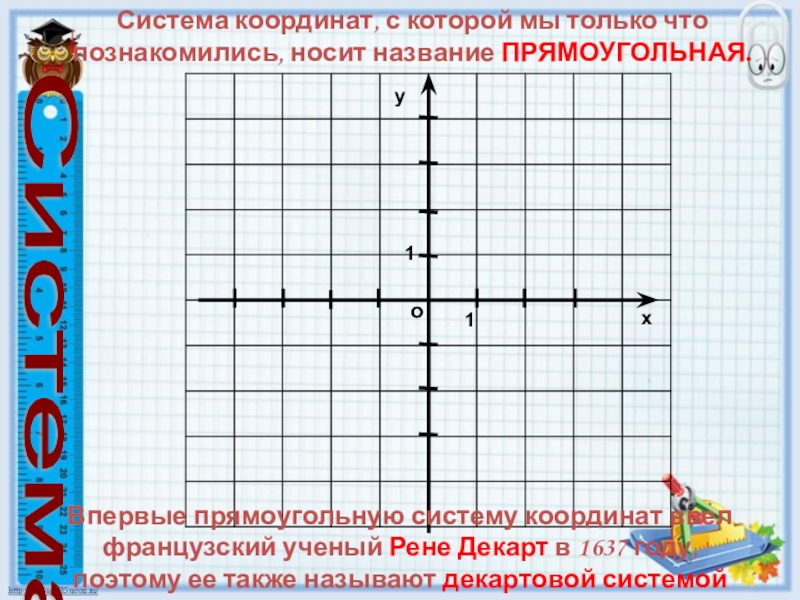
Система координат, с которой мы только что познакомились, носит название
Впервые прямоугольную систему координат ввел французский ученый Рене Декарт в 1637 году, поэтому ее также называют декартовой системой координат.
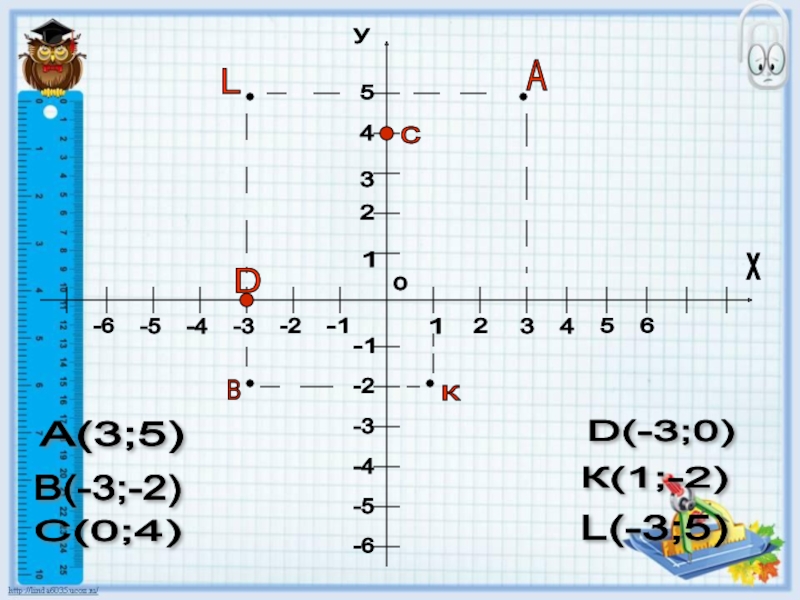
Слайд 11y
х
о
1
2
3
4
5
6
5
1
2
3
4
-1
-2
-3
-4
-5
-6
-1
-2
-3
-5
-4
-6
А
В
с
D
к
L
А(3;5)
В(-3;-2)
С(0;4)
D(-3;0)
К(1;-2)
L(-3;5)
Слайд 12
А
G
С
F
1
D
Е
В
К
(-3; 0)
(0; 3)
(3; 0)
(0;-3)
P
(0; 2)
(-2; 0)
(0;-2)
(2; 0)
O
(-2; 0)
(0;-2)
(2; 0)
(0; 2)
N
(0; 3)
(3;
(-3; 0)
(0;-3)
M
(2;-4)
(2; 4)
(4; 2)
(4;-2)
K
(-2; 2)
(-2;-2)
(2;-2)
(2; 2)
G
(1; 4)
(4;-1)
(1;-4)
(-1; 4)
F
(2;-4)
(-2; -4)
(2; 4)
(-4;-2)
E
(-4; 2)
(2;-4)
(4;-2)
(-4; -2)
D
(-2; 2)
(-2;-2)
(2;-2)
(2; 2)
C
(4;1)
(1;-4)
(1; 4)
(-4; 1)
B
(-2;-2)
(-2;2)
(2;2)
(2;-2)
А
N
O
M
P
(Х;У)
(Х;У)
(Х;У)
(Х;У)
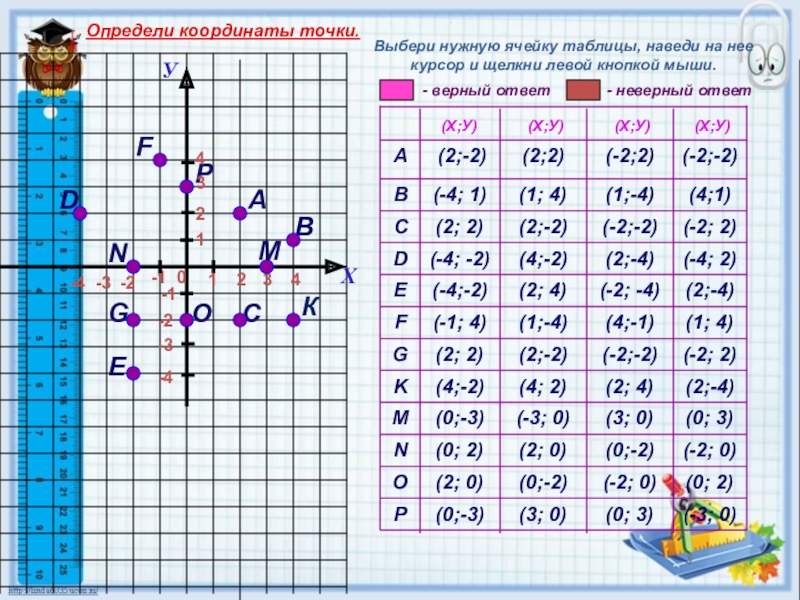
Выбери нужную ячейку таблицы, наведи на нее курсор и щелкни левой кнопкой мыши.
- верный ответ - неверный ответ
Определи координаты точки.
-2
-3
-4
2
3
4
-2
-3
-4
0
Слайд 13Х
У
0
1
(1;7)
(2;0)
(-5;4)
(0;-3)
(7;-5)
(-7;0)
(-6;-4)
(0;1)
(0;5)
(3;-4)
(0:-8)
(5;3)
(-4;0)
(-3;-5)
(9;0)
(-2;9)
1
-1
-1
2
3
9
4
6
-5
7
8
-2
3
2
4
5
6
7
8
9
-3
-4
5
-6
-7
-3
-2
-4
-6
-5
-7
-8
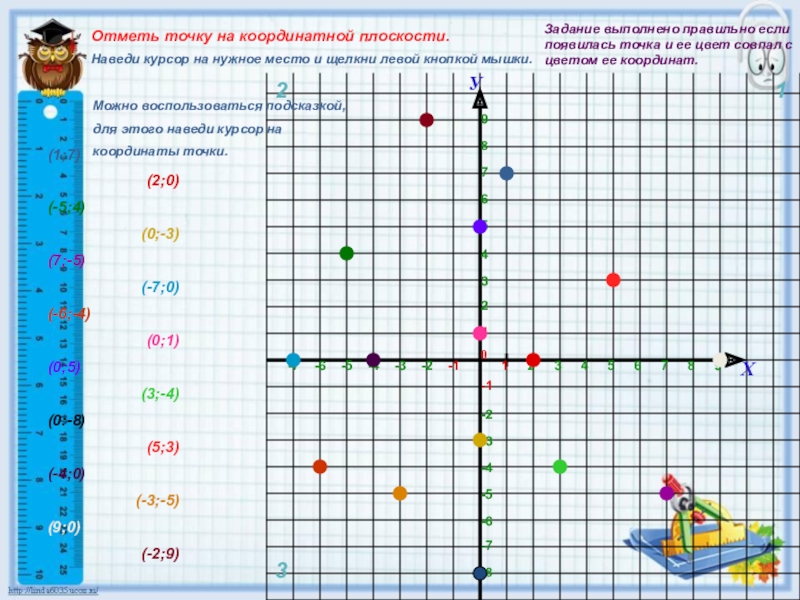
Отметь точку на координатной плоскости.
Наведи курсор на нужное место и щелкни
Можно воспользоваться подсказкой,
для этого наведи курсор на
координаты точки.
Задание выполнено правильно если появилась точка и ее цвет совпал с цветом ее координат.
1
3
2
Слайд 14
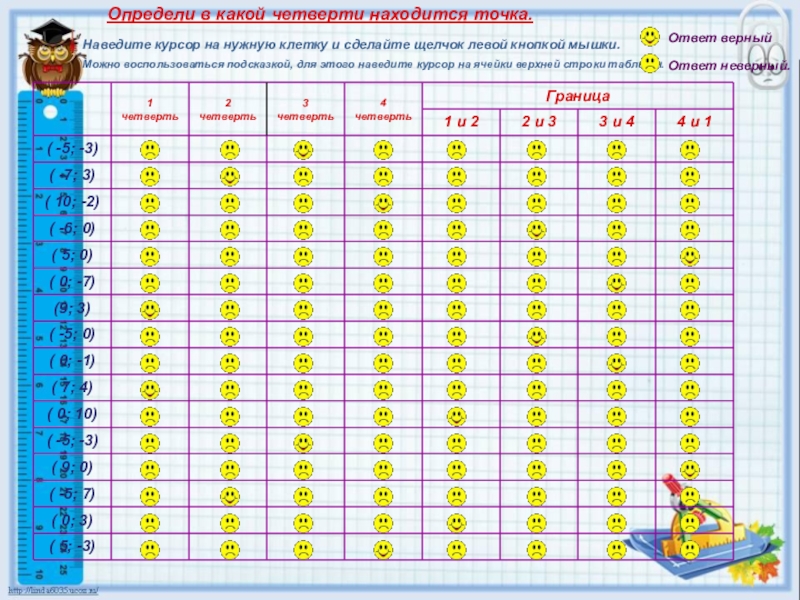
Определи в какой четверти находится точка.
( 5; -3)
( 0; 3)
( -5;
( 9; 0)
( -5; -3)
( 0; 10)
( 7; 4)
( 0; -1)
( -5; 0)
(9; 3)
( 0; -7)
( 5; 0)
( -6; 0)
( 10; -2)
( -7; 3)
( -5; -3)
4 и 1
3 и 4
2 и 3
1 и 2
Граница
4 четверть
3 четверть
2 четверть
1 четверть
Наведите курсор на нужную клетку и сделайте щелчок левой кнопкой мышки.
Можно воспользоваться подсказкой, для этого наведите курсор на ячейки верхней строки таблицы.
Ответ верный
Ответ неверный.
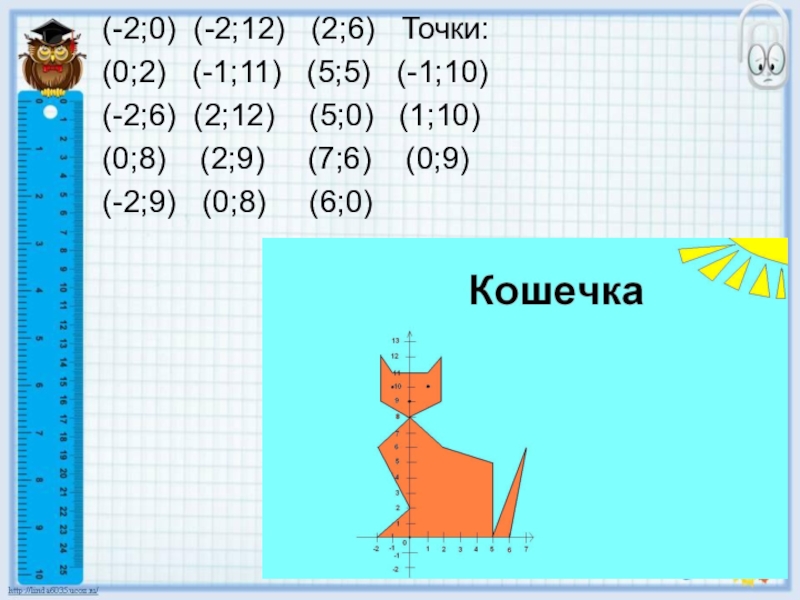
Слайд 15(-2;0) (-2;12) (2;6) Точки:
(0;2) (-1;11) (5;5)
(-2;6) (2;12) (5;0) (1;10)
(0;8) (2;9) (7;6) (0;9)
(-2;9) (0;8) (6;0)