- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по теме: Комплексные числа
Содержание
- 1. Презентация по теме: Комплексные числа
- 2. N c Z c
- 3. Z = a + b ia, b
- 4. КОМПЛЕКСНЫМИ ЧИСЛАМИ НАЗЫВАЮТ СУММУ
- 5. Действия над комплексными числамиСравнение: a + bi
- 6. Сумма a+bi (a и b действительные числа)а
- 7. Минимальные условия комплексного числа.1)Существует число, квадрат которого
- 8. КОМПЛЕКСНЫЕ ЧИСЛА РАВНЫ, КОГДА РАВНЫ ИХ ДЕЙСТВИТЕЛЬНЫЕ
- 9. Геометрическая модель.Комплексная плоскость состоит из двух осей:Re
- 10. 0CIm zRe zba
- 11. В этом наглядном представлении сумма комплексных чисел
- 12. Спасибо за внимание!
- 13. Используемая литература в интернете: http://ru.wikipedia.org/wiki/%CA%EE%EC%EF%EB%E5%EA%F1%ED%EE%E5_%F7%E8%F1%EB%EEhttp://www.mathprofi.ru/kompleksnye_chisla_dlya_chainikov.html
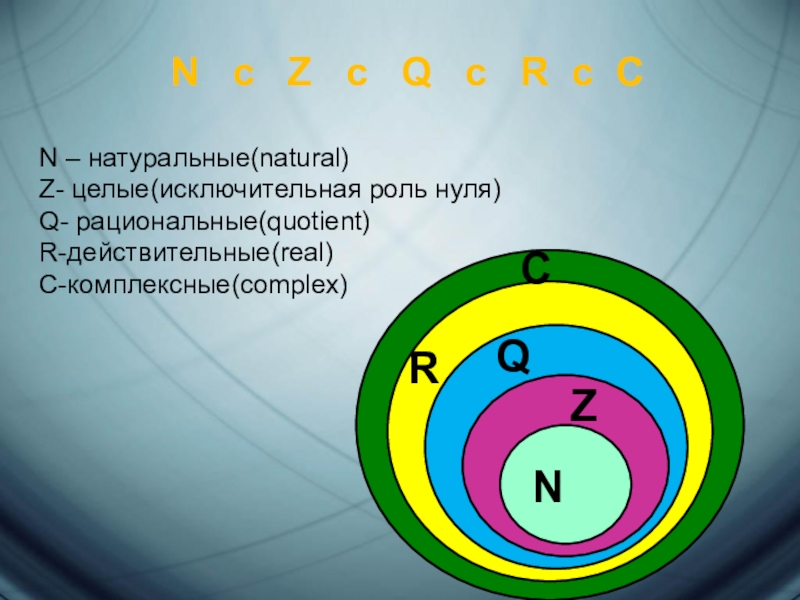
Слайд 2N c Z c Q c
N – натуральные(natural)
Z- целые(исключительная роль нуля)
Q- рациональные(quotient)
R-действительные(real)
C-комплексные(complex)
С
R
Q
Z
N
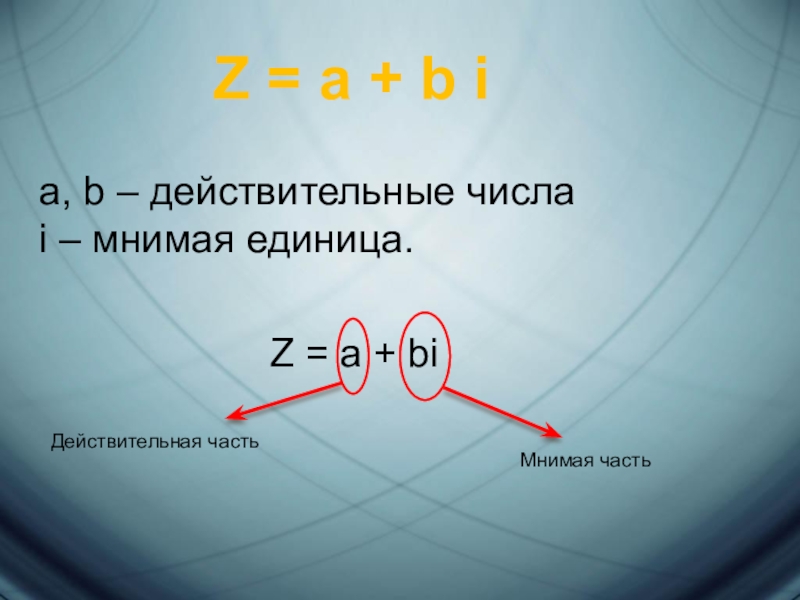
Слайд 3Z = a + b i
a, b – действительные числа
i –
Z = a + bi
Действительная часть
Мнимая часть
Слайд 4
КОМПЛЕКСНЫМИ ЧИСЛАМИ НАЗЫВАЮТ СУММУ ДЕЙСТВИТЕЛЬНОГО ЧИСЛА И ЧИСТО
Z=a + bi
Правило:
Слайд 5Действия над комплексными числами
Сравнение: a + bi = c + di.
Сложение:
Вычитание:(a + bi) – (c + di) = (a – c) + (b – d )i
Умножение: (a + bi) • ( c + bi) = ac + bci + adi + bdi² = (ac – b d)
Деление: a + bi = (a+bi)(c – di) = ac + bd + bc - ad
c + di (c + di)(c – di) c² = d² c² + d²
Слайд 6Сумма a+bi (a и b действительные числа)
а = 0, то a+bi
b = 0, то a+bi =а+0=а ( действительное)
а не равно нулю, то a+bi ни действительное, не мнимое. Оно более сложное составное число.
Слайд 7Минимальные условия комплексного числа.
1)Существует число, квадрат которого = -1.
2)Множество комплексных
Слайд 8КОМПЛЕКСНЫЕ ЧИСЛА РАВНЫ, КОГДА РАВНЫ ИХ ДЕЙСТВИТЕЛЬНЫЕ И МНИМЫЕ ЧАСТИ.
a+bi=c+di,
Так же главное знать, что:
i²= -1.
Слайд 9Геометрическая модель.
Комплексная плоскость состоит из двух осей:
Re z –действительная ось,
Im z
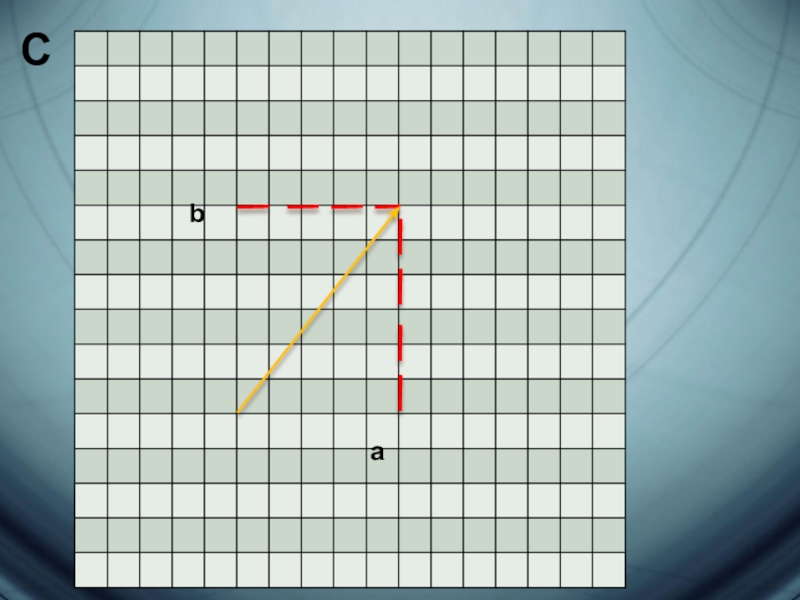
Рассмотрим плоскость с прямоугольной системой координат. Каждому комплексному числу z = a + bi сопоставим точку плоскости с координатами {a;b}.
Слайд 11В этом наглядном представлении сумма комплексных чисел соответствует векторной сумме соответствующих радиус-векторов. При
Геометрическая модель комплексных чисел широко используется в планиметрии: многие планиметрические теоремы можно доказать как некоторые комплексные тождества. Часто этот метод даёт наиболее простое доказательство.