- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по теме Элементы комбинаторики
Содержание
- 1. Презентация по теме Элементы комбинаторики
- 2. Историческая справкаТермин «комбинаторика»
- 3. КОМБИНАТОРИКА изучаеткомбинации предметовперестановки предметовПеребор возможных вариантов
- 4. Сочетания ПерестановкиРазмещенияКОМБИНАТОРНЫЕ ЗАДАЧИ
- 5. ПЕРЕСТАНОВКИПерестановкой из n элементов называется каждое расположение этих элементов определенном порядке.Р n = n!=1∙2∙3∙…∙n
- 6. Задача. К кассе зоопарка одновременно подошли 5
- 7. СОЧЕТАНИЯСочетанием из n элементов по k называется
- 8. ❷ ❸ ❹ ❺❷ ❸ ❹ ❺Задача.
- 9. Решение. Согласно условию задачи, две кнопки должны
- 10. РАЗМЕЩЕНИЯРазмещением из n элементов по k называется
- 11. Задача. Ученики класса изучают 8 предметов. Сколькими
- 12. Слайд 12
- 13. Студенческая группа состоит
- 14. Студенческая группа состоит из 23 человек, среди
- 15. Какие трехзначные числа
- 16. Маша, Оля, Вера, Ира, Андрей, Миша
- 17. Спасибо за внимание!
Историческая справкаТермин «комбинаторика» происходит от латинского слова «combinare», что в переводе на русский означает – «сочетать», «соединять».
Слайд 2 Историческая справка
Термин «комбинаторика» происходит от латинского слова
«combinare», что в переводе на русский означает – «сочетать», «соединять».
Слайд 5ПЕРЕСТАНОВКИ
Перестановкой из n элементов называется каждое расположение этих элементов определенном порядке.
Р
n = n!=1∙2∙3∙…∙n
Слайд 6Задача. К кассе зоопарка одновременно подошли 5 человек. Сколькими способами они
могут выстроиться в очередь?
Решение: у нас есть множество, состоящее из 5 элементов. Нам нужно подсчитать количество расположений этих элементов на 5 местах, то есть определить число перестановок 5 элементов. Это число равно 5!=1∙2∙3∙4∙5=120
Решение: у нас есть множество, состоящее из 5 элементов. Нам нужно подсчитать количество расположений этих элементов на 5 местах, то есть определить число перестановок 5 элементов. Это число равно 5!=1∙2∙3∙4∙5=120
Слайд 7СОЧЕТАНИЯ
Сочетанием из n элементов по k называется любое множество, составленное из
k элементов, выбранных из n элементов.
Слайд 8❷ ❸ ❹ ❺
❷ ❸ ❹ ❺
Задача. Возвращаясь с прогулки, Петя
обнаружил, что он забыл код замка от двери подъезда. Он помнит, что замок открывается одновременным нажатием трех кнопок из десяти, которые расположены в два ряда по пять штук в каждом, причем две кнопки должны быть нажаты в верхнем ряду, а одна – в нижнем. Какое максимальное число комбинаций должен перебрать Петя, чтобы открыть дверь?
Слайд 9Решение. Согласно условию задачи, две кнопки должны быть одновременно нажаты в
ряду, состоящем из пяти кнопок. Количество выборок из 5 элементов по два равно С52=5!/(2!(5-2)!) =1∙2∙3∙4∙5/1∙2∙1∙2∙3=10
Следовательно, количество комбинаций нажатия двух кнопок в первом ряду равно 10.
Количество способов, которыми можно нажать одну кнопку в нижнем ряду
С51=5!/(1!(5-1)!) =1∙2∙3∙4∙5/1∙1∙2∙3∙4=5
Значит, максимальное количество комбинаций, которые должен перебрать Петя, чтобы открыть замок, равно
10∙5=50
Следовательно, количество комбинаций нажатия двух кнопок в первом ряду равно 10.
Количество способов, которыми можно нажать одну кнопку в нижнем ряду
С51=5!/(1!(5-1)!) =1∙2∙3∙4∙5/1∙1∙2∙3∙4=5
Значит, максимальное количество комбинаций, которые должен перебрать Петя, чтобы открыть замок, равно
10∙5=50
Слайд 10РАЗМЕЩЕНИЯ
Размещением из n элементов по k называется любое множество, состоящее из
любых k элементов, взятых в определенном порядке из данных n элементов .
Слайд 11Задача. Ученики класса изучают 8 предметов. Сколькими способами можно составить расписание
на один день, чтобы в нем было 4 различных предмета?
Решение
Решение
Слайд 13 Студенческая группа состоит из 23 человек, среди которых 10 юношей и
13 девушек. Сколькими способами можно выбрать 2-х человек одного пола?
Решение:
способами можно выбрать 2-х юношей;
способами можно выбрать 2-х девушек.
Таким образом, двух человек одного пола (без разницы – юношей или девушек) можно выбрать: способами.
Ответ: 123
Слайд 14Студенческая группа состоит из 23 человек, среди которых 10 юношей и
13 девушек. Сколькими способами можно составить пару из юноши и девушки?
Решение: способами можно выбрать 1 юношу;
способами можно выбрать 1 девушку.
Таким образом, 1-го юношу и 1 девушку можно выбрать: способами.
Ответ: 130 способов
Слайд 15
Какие трехзначные числа можно составить из цифр 0, 2, 4?
Решение. Построим
дерево возможных вариантов, учитывая, что 0 не может быть первой цифрой в числе.
Ответ: 200, 202, 204, 220, 222, 224, 240, 242, 244, 400, 402, 404, 420, 422, 424, 440, 442, 444.
Ответ: 200, 202, 204, 220, 222, 224, 240, 242, 244, 400, 402, 404, 420, 422, 424, 440, 442, 444.
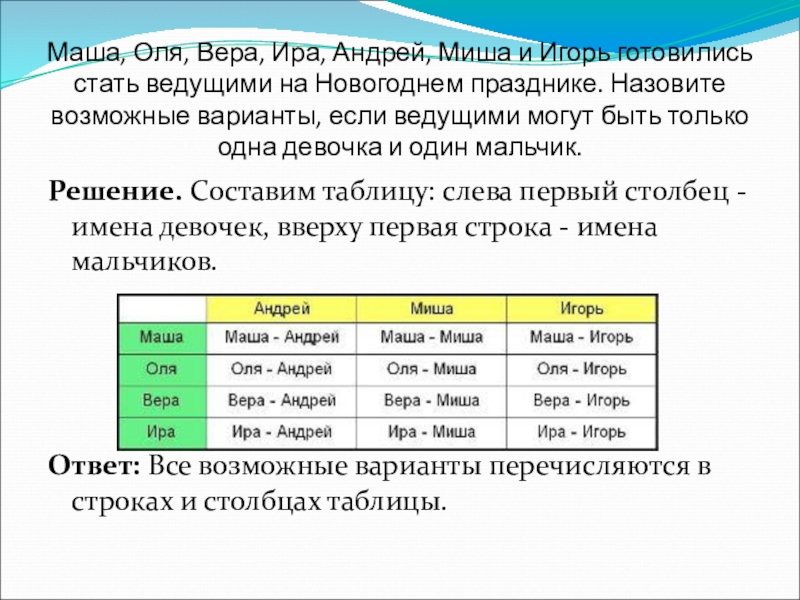
Слайд 16 Маша, Оля, Вера, Ира, Андрей, Миша и Игорь готовились стать ведущими
на Новогоднем празднике. Назовите возможные варианты, если ведущими могут быть только одна девочка и один мальчик.
Решение. Составим таблицу: слева первый столбец - имена девочек, вверху первая строка - имена мальчиков.
Ответ: Все возможные варианты перечисляются в строках и столбцах таблицы.
