- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по математики Пирамида
Содержание
- 1. Презентация по математики Пирамида
- 2. ПирамидаСлово «пирамида» в геометрию ввели греки, которые,
- 3. ОпределениеПирамида — многогранник, в основании которого лежит многоугольник, а
- 4. ACDEHBSВершинаРёбраОснованиеOВысота пирамидыПирамида Боковая граньВысота боковой граниАпофема
- 5. Определение апофема — высота боковой грани правильной пирамиды, которая
- 6. По количеству углов основания пирамиды делят на
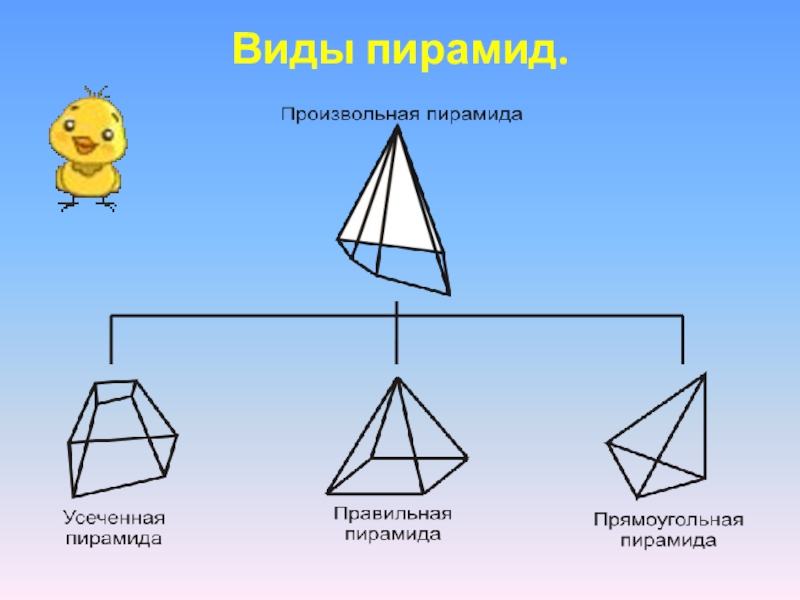
- 7. Виды пирамид.
- 8. Усеченная пирамида Это многогранник, образованный пирамидой и её сечением, параллельным основаниюSполн= S1+S2+Sбок
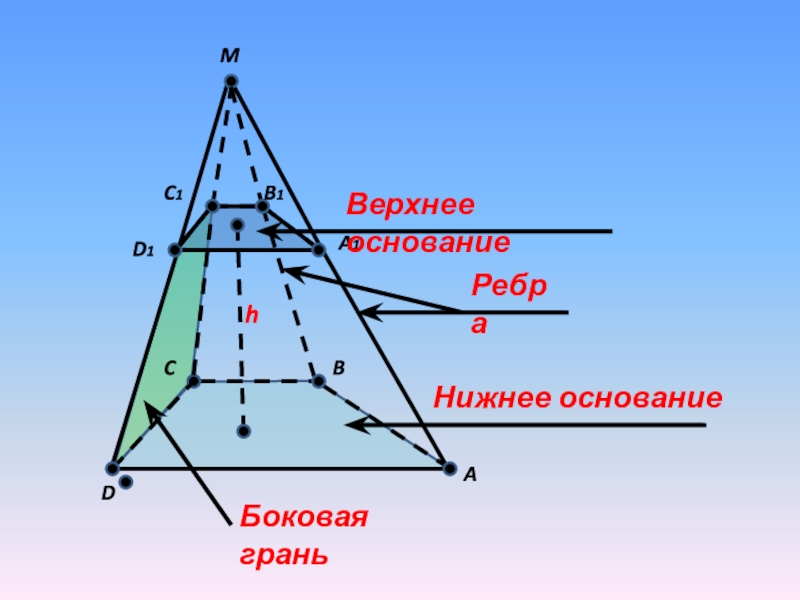
- 9. MCBD1DAC1A1B1Верхнее основаниеНижнее основаниеРебраБоковая граньh
- 10. Правильная пирамидаПирамида, основанием которой является правильный многоугольник, а вершина которой проектируется в центр основания.
- 11. Свойства правильной пирамидыБоковые ребра правильной пирамиды равны
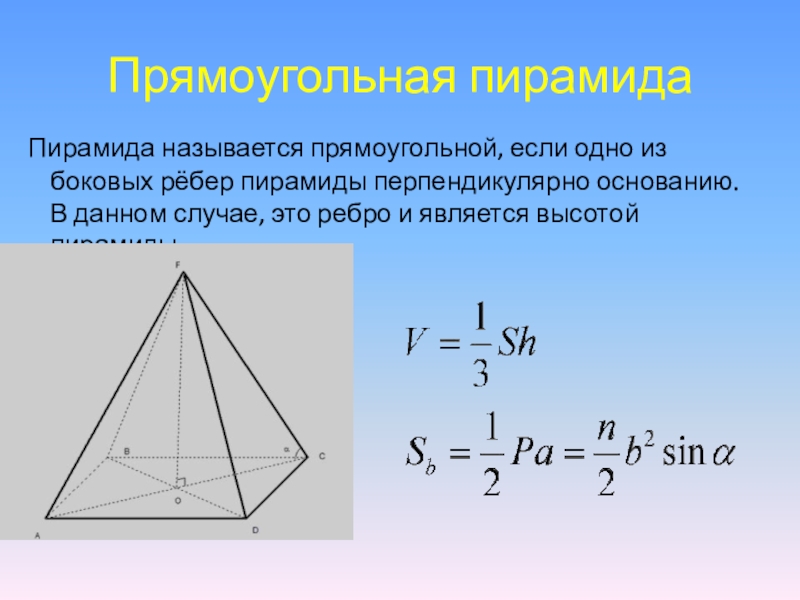
- 12. Прямоугольная пирамида Пирамида называется прямоугольной, если одно
- 13. ЗадачаЗадача № 1.Существует ли тетраэдр, у которого пять углов граней – прямые?
- 14. Задача № 2.Изобразите тетраэдр DABC и на
- 15. ЗадачаЗадача № 3Изобразите тетраэдр KLMNи постройте
- 16. ЗадачаЗадача № 4.Изобразите тетраэдр DABC отметьте точки
- 17. Задачи Задача № 5.Докажите, что площадь боковой
- 18. Домашнее задание Изучить конспект урока;Решить задачи № 1211(а), 1207.
- 19. Домашние задачи1211 Найдите объем пирамиды с высотой
- 20. Презентация подготовлена по материалам сайта http://ru.wikipedia.org учебника
- 21. Спасибо за внимание
Слайд 2Пирамида
Слово «пирамида» в геометрию ввели греки, которые, как полагают, заимствовали его
Слайд 3Определение
Пирамида — многогранник, в основании которого лежит многоугольник, а остальные грани являются треугольниками, которые
Слайд 4A
C
D
E
H
B
S
Вершина
Рёбра
Основание
O
Высота пирамиды
Пирамида
Боковая грань
Высота боковой грани
Апофема
Слайд 5Определение
апофема — высота боковой грани правильной пирамиды, которая проведена из ее вершины
боковые грани — треугольники, которые сходятся в вершине;
боковые ребра — общие стороны боковых граней;
вершина пирамиды — точка, которая соединяет боковые ребра и которая не лежит в плоскости основания;
высота — отрезок перпендикуляра, который проведен через вершину пирамиды к плоскости ее основания (концами такого отрезка будут вершина пирамиды и основание перпендикуляра);
диагональное сечение пирамиды — сечение пирамиды, которое проходит через вершину и диагональ основания;
основание — многоугольник, которому не принадлежит вершина пирамиды.
Слайд 6По количеству углов основания пирамиды делят на треугольные, четырехугольные и так
Пирамида будет треугольной, четырехугольной, и так далее, когда основанием пирамиды будет треугольник, четырехугольник и так далее. Треугольная пирамида есть четырехгранник — тетраэдр. Четырехугольная — пятигранник и так далее.
Слайд 8Усеченная пирамида
Это многогранник, образованный пирамидой и её сечением, параллельным основанию
Sполн= S1+S2+Sбок
Слайд 10Правильная пирамида
Пирамида, основанием которой является правильный многоугольник, а вершина которой проектируется в центр
Слайд 11Свойства правильной пирамиды
Боковые ребра правильной пирамиды равны между собой.
Боковые грани правильной
Апофемы правильной пирамиды равны.
В любую правильную пирамиду можно как вписать, так и описать около неё сферу.
Все боковые грани образуют с плоскостью основания правильной пирамиды равные углы.
Слайд 12Прямоугольная пирамида
Пирамида называется прямоугольной, если одно из боковых рёбер пирамиды
Слайд 14Задача № 2.
Изобразите тетраэдр DABC и на ребрах DB, DC и
Задача
Прямая МN принадлежит плоскости BCD которая пересекается с плоскостью ABC по BC. Продолжим BC до пересечения с прямой MN в точке Х Точка Х принадлежит и прямой MN, и плоскости ABC, так как точка Х лежит на прямой BC, принадлежащей плоскости ABC.
Слайд 15
Задача
Задача № 3
Изобразите тетраэдр KLMNи постройте сечение этого тетраэдра плоскостью, проходящей
Решение:
По условию MA=NA Проводим отрезок AL, так как точки L и A принадлежат одной плоскости MNL. Проводим отрезок AK, так как точки K и A принадлежат одной плоскости MKN. Искомое сечение – треугольник AKL.
Слайд 16Задача
Задача № 4.
Изобразите тетраэдр DABC отметьте точки M и N на
Решение:
1. Проводим прямую MN, продолжаем AB до пересечения с прямой MN в точке X.
2. Точка X принадлежит плоскости ABC, и точка K принадлежит плоскости ABC, тогда проводим прямую XK, пересекающую прямые BC и AC в точках P и H соответственно.
3. Проводим отрезки MP, NH и PH. Четырехугольник PMNH – искомое сечение.
Слайд 17Задачи
Задача № 5.
Докажите, что площадь боковой поверхности правильной
пирамиды (т. е.
половине произведения периметра основания на апофему.
Задача № 6.
Основанием пирамиды является параллелограмм со сторонами 5 м и 4 м и меньшей диагональю 3 м. Высота пирамиды проходит через точку пересечения диагоналей основания и равна 2 м. Найдите площадь поверхности пирамиды, т. е. сумму площадей всех ее граней.
Слайд 19Домашние задачи
1211 Найдите объем пирамиды с высотой h, если: а) h=2
1207 Основанием пирамиды является ромб, сторона которого равна 5 см, а одна из диагоналей равна 8 см. Найдите боковые ребра пирамиды, если ее высота проходит через точку пересечения диагоналей основания и равна 7 см.