- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по математики на тему Конус
Содержание
- 1. Презентация по математики на тему Конус
- 2. Сабақтың мақсатыОқушыларға конус және оның элементтері туралы
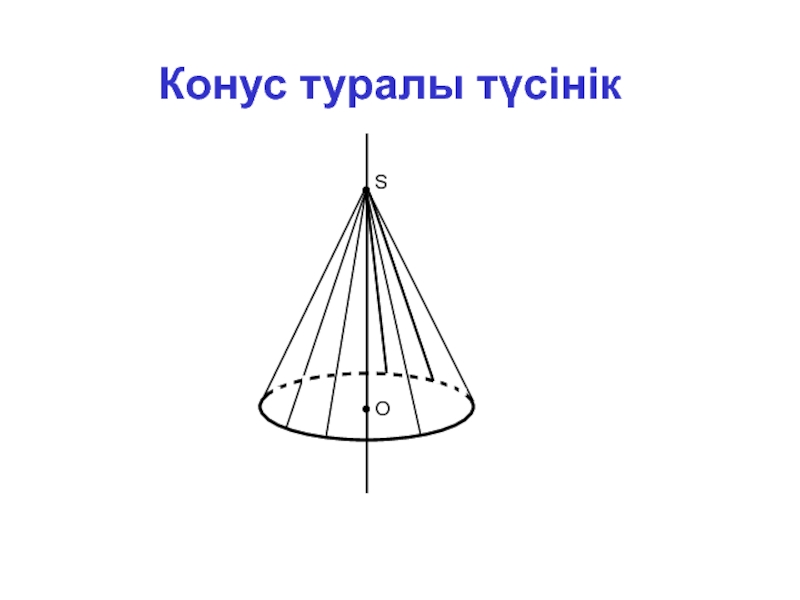
- 3. ОS Конус туралы түсінік
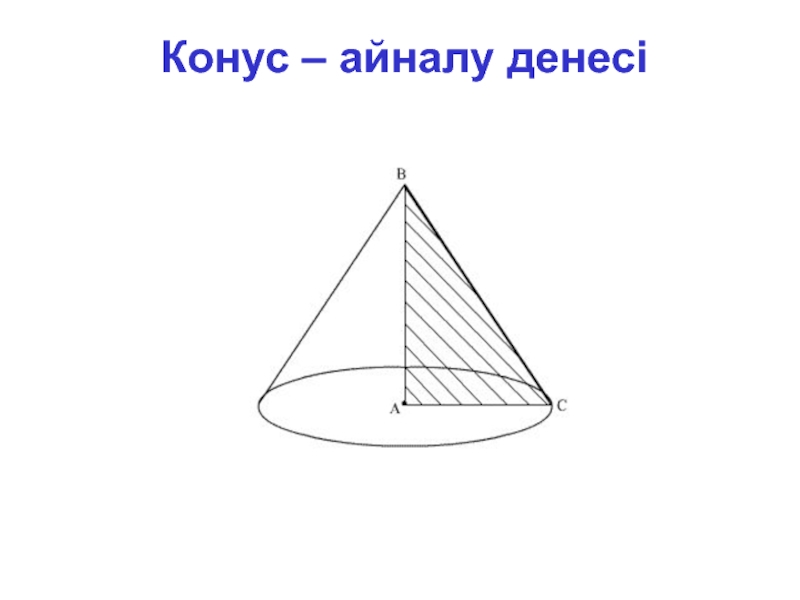
- 4. Конус – айналу денесі
- 5. Анықтама. Тікбұрышты үшбұрышты катетінен айналдырғанда шығатын денені конус деп атайды.
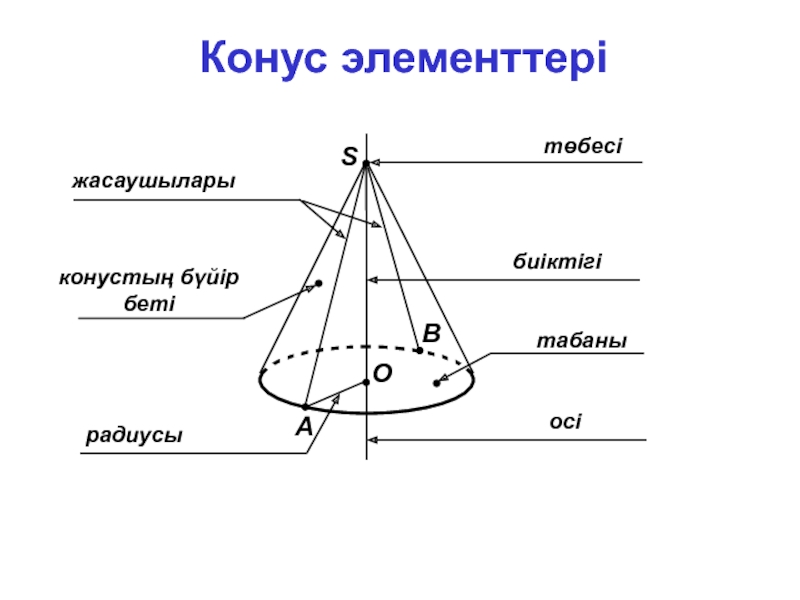
- 6. ОSАВтабанырадиусыжасаушыларыконустың бүйір бетітөбесібиіктігіосіКонус элементтері
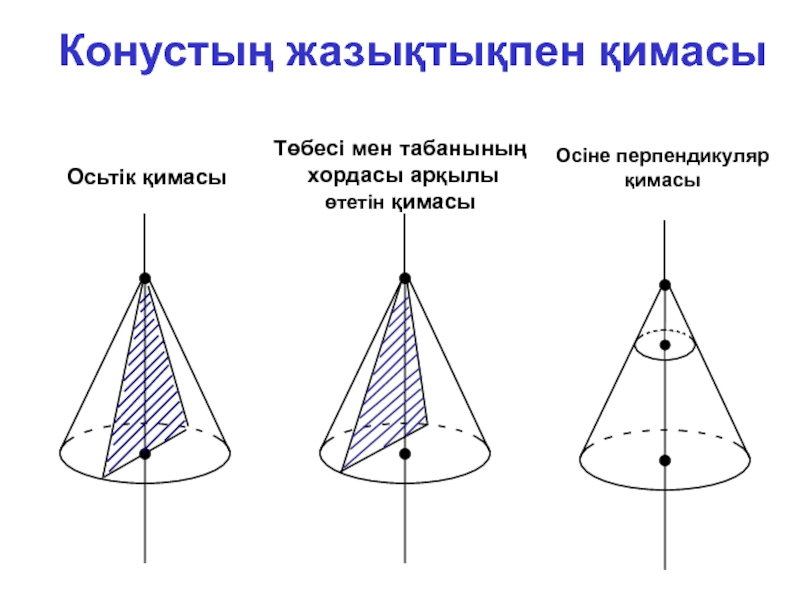
- 7. Конустың жазықтықпен қимасыОсьтік қимасыТөбесі мен табанының хордасы арқылы өтетін қимасыОсіне перпендикуляр қимасы
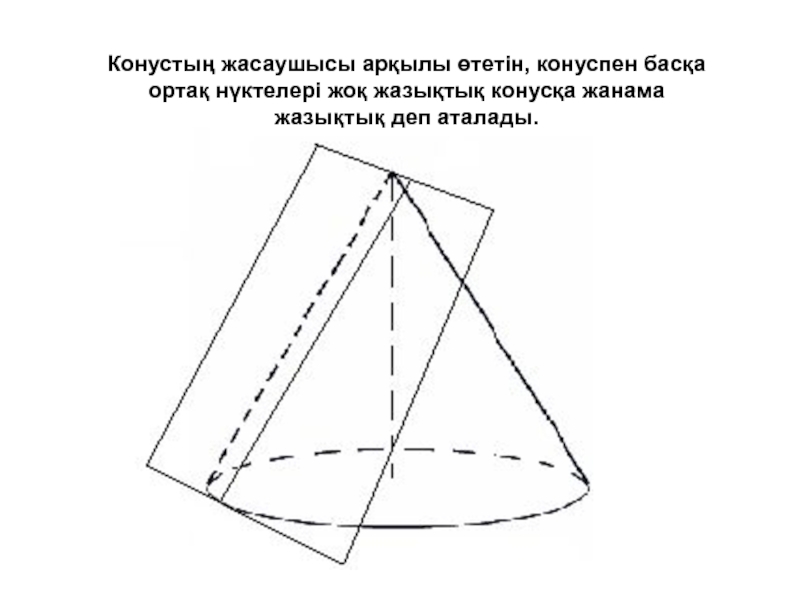
- 8. Конустың жасаушысы арқылы өтетін, конуспен басқа ортақ нүктелері жоқ жазықтық конусқа жанама жазықтық деп аталады.
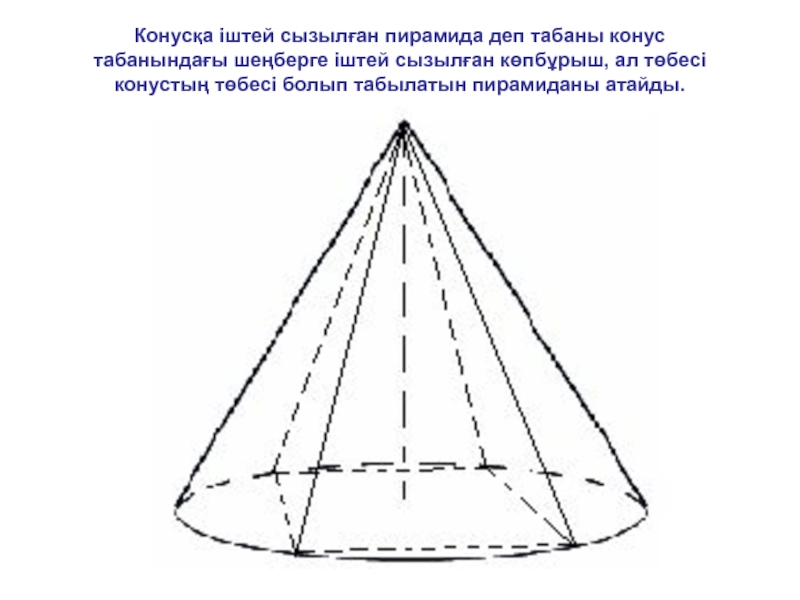
- 9. Конусқа іштей сызылған пирамида деп табаны конус
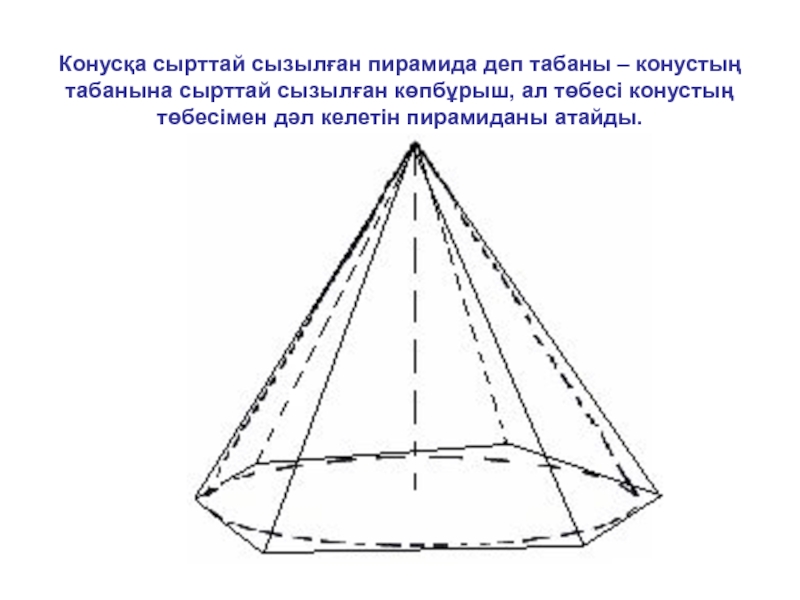
- 10. Конусқа сырттай сызылған пирамида деп табаны –
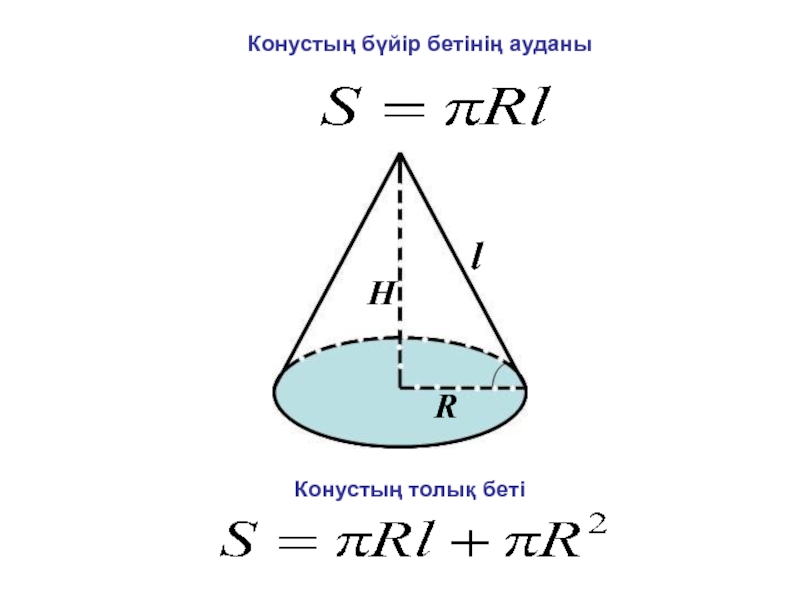
- 11. HlRКонустың бүйір бетінің ауданыКонустың толық беті
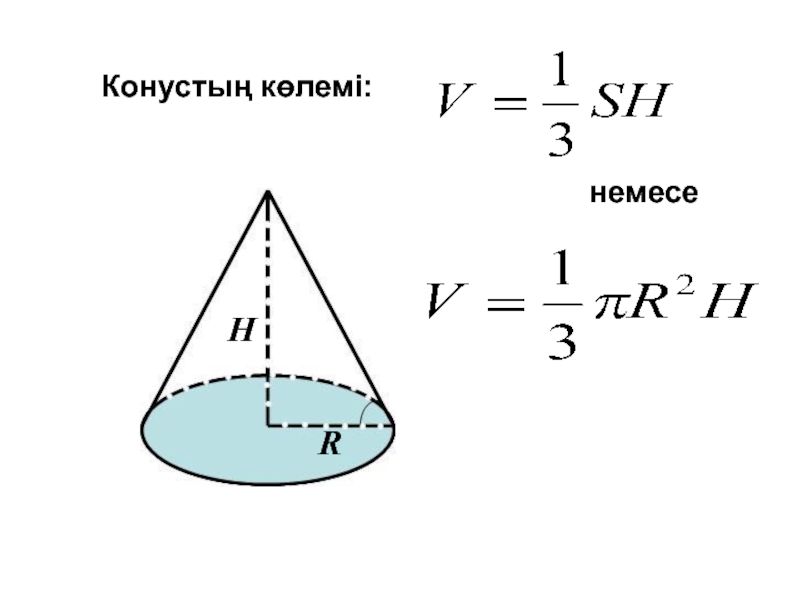
- 12. RHКонустың көлемі:
- 13. Есеп №1. Конустың жасаушысы 12 дм және
- 14. Есеп №2. Конус биіктігі 20 см, табанының радиусы 15 см. Бүйір бетінің ауданын табыңыз.HRl
- 15. Есеп №4. Конустың жасаушысы 5 см, табанының радиусы 4 см. Толық бетінің ауданын табыңыз.5 см4 см
- 16. Есеп №4. Конустың биіктігі 15 м, ал
- 17. Есеп №5. Конустың жасаушысы
- 18. Есеп №6. Конустың осьтік қимасы гипотенузасы 8
- 19. O
Сабақтың мақсатыОқушыларға конус және оның элементтері туралы түсінік беру.Конустың бүйір бетін, толық бетін, көлемін табуға байланысты тесттік есептерді шығаруға жаттықтыру.Оқушылардың ойлау қабілетін арттыру, ұқыптылыққа, нақтылыққа тәрбиелеу.
Слайд 2Сабақтың мақсаты
Оқушыларға конус және оның элементтері туралы түсінік беру.
Конустың бүйір бетін,
толық бетін, көлемін табуға байланысты тесттік есептерді шығаруға жаттықтыру.
Оқушылардың ойлау қабілетін арттыру, ұқыптылыққа, нақтылыққа тәрбиелеу.
Оқушылардың ойлау қабілетін арттыру, ұқыптылыққа, нақтылыққа тәрбиелеу.
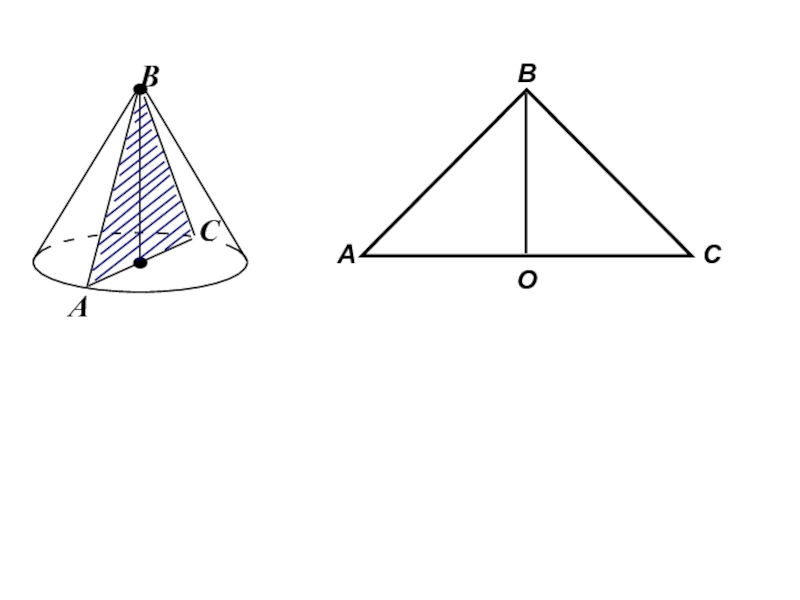
Слайд 7Конустың жазықтықпен қимасы
Осьтік қимасы
Төбесі мен табанының
хордасы арқылы
өтетін қимасы
Осіне перпендикуляр
қимасы
Слайд 8Конустың жасаушысы арқылы өтетін, конуспен басқа ортақ нүктелері жоқ жазықтық конусқа
жанама жазықтық деп аталады.
Слайд 9Конусқа іштей сызылған пирамида деп табаны конус табанындағы шеңберге іштей сызылған
көпбұрыш, ал төбесі конустың төбесі болып табылатын пирамиданы атайды.
Слайд 10Конусқа сырттай сызылған пирамида деп табаны – конустың табанына сырттай сызылған
көпбұрыш, ал төбесі конустың төбесімен дәл келетін пирамиданы атайды.
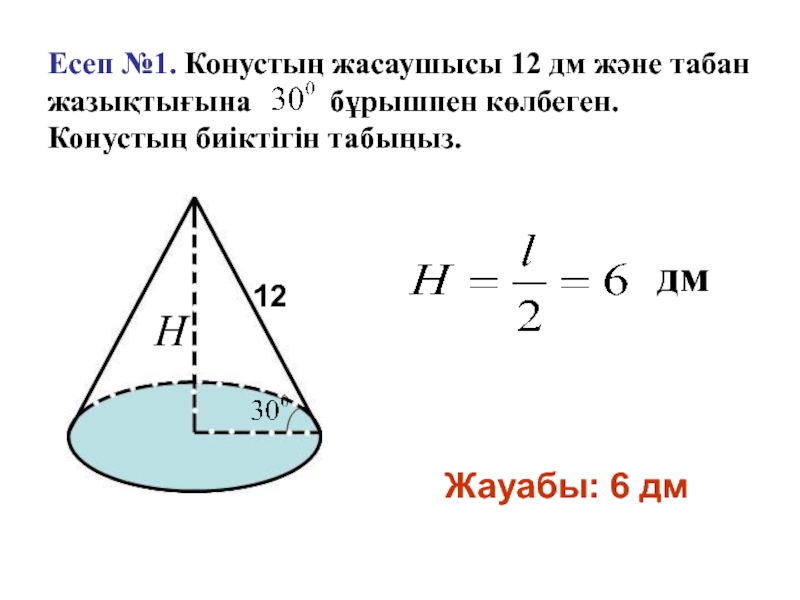
Слайд 13Есеп №1. Конустың жасаушысы 12 дм және табан жазықтығына
бұрышпен көлбеген. Конустың биіктігін табыңыз.
12
Жауабы: 6 дм
H
Слайд 15Есеп №4. Конустың жасаушысы 5 см, табанының радиусы 4 см. Толық
бетінің ауданын табыңыз.
5 см
4 см
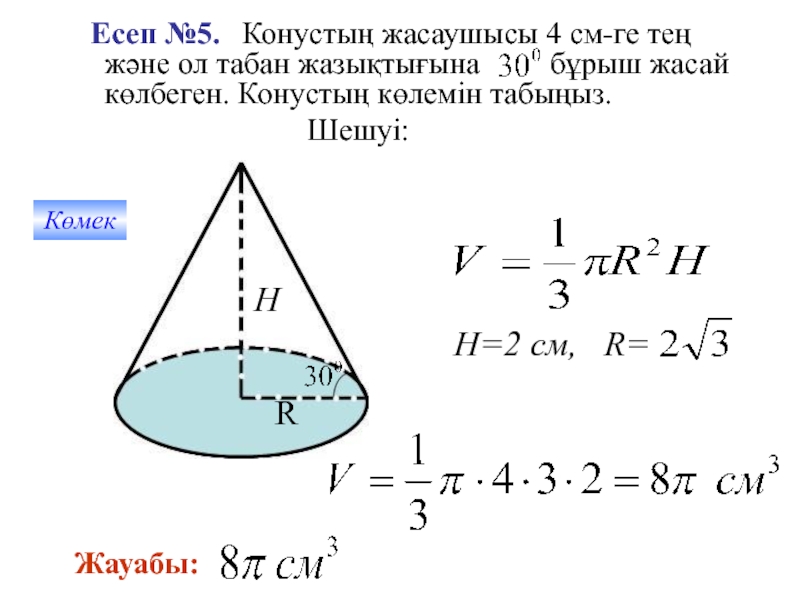
Слайд 17 Есеп №5. Конустың жасаушысы 4 см-ге тең және
ол табан жазықтығына бұрыш жасай көлбеген. Конустың көлемін табыңыз.
Шешуі:
Шешуі:
R
4 cм
H
R
Көмек
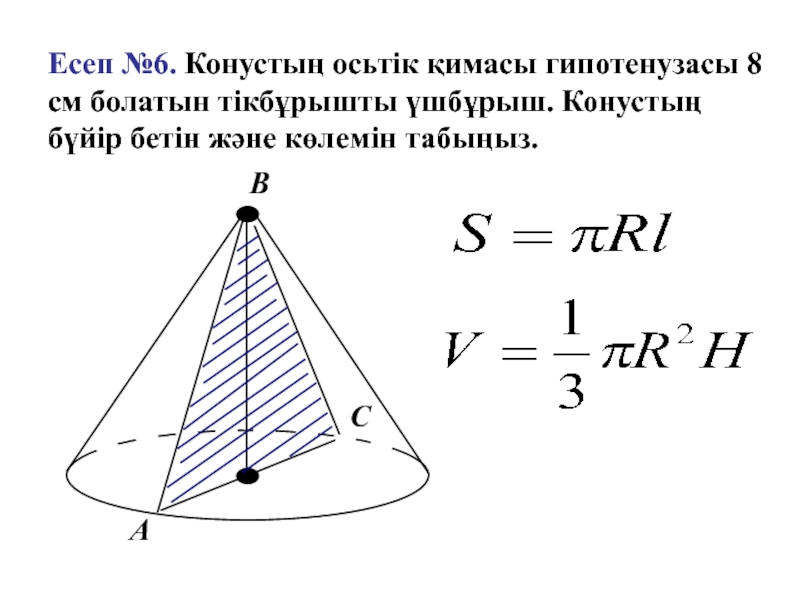
Слайд 18Есеп №6. Конустың осьтік қимасы гипотенузасы 8 см болатын тікбұрышты үшбұрыш.
Конустың бүйір бетін және көлемін табыңыз.