- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по математике:Решение не стантандартных задач (5-7 классы)
Содержание
- 1. Презентация по математике:Решение не стантандартных задач (5-7 классы)
- 2. Нестандартные задачи1 тип. Задачи на смекалку.1.Масса цапли,
- 3. 2 тип. Занимательные задачи.Как расставить 6 стульев
- 4. 3 тип. Геометрические задачи.1.Раздели пирог прямоугольной формы
- 5. 2 тип. Логические квадраты.1.Заполни квадрат (4 х
- 6. 5 тип. Комбинаторные задачи.1.У Даши 2 юбки:
- 7. 6 тип. Задачи на переливание.1. Можно ли,
- 8. 1.сведение путем преобразований нестандартной задачи к другой,
- 9. ПримерРассмотрим на примере задачи: По тропинке, вдоль
- 10. Правила 1.«Простое» правило: не пропустите самую простую
- 11. примерЗадача №3.У моста через речку встретились лодырь
- 12. Методика формирования умения решать нестандартные задачи.Задача№1. -
- 13. Задача № 2. -В гараже стояли
Нестандартные задачи1 тип. Задачи на смекалку.1.Масса цапли, стоящей на одной ноге 12 кг. Сколько будет весить цапля, если встанет на 2 ноги?2.Пара лошадей пробежала 40 км. Сколько пробежала каждая лошадь?3.У семи братьев по одной сестре. Сколько
Слайд 2Нестандартные задачи
1 тип. Задачи на смекалку.
1.Масса цапли, стоящей на одной ноге
12 кг. Сколько будет весить цапля, если встанет на 2 ноги?
2.Пара лошадей пробежала 40 км. Сколько пробежала каждая лошадь?
3.У семи братьев по одной сестре. Сколько всего детей в семье?
4.Шесть котов за шесть минут съедают шесть мышей. Сколько понадобится котов, чтобы за сто минут съесть сто мышей?
2.Пара лошадей пробежала 40 км. Сколько пробежала каждая лошадь?
3.У семи братьев по одной сестре. Сколько всего детей в семье?
4.Шесть котов за шесть минут съедают шесть мышей. Сколько понадобится котов, чтобы за сто минут съесть сто мышей?
Слайд 32 тип. Занимательные задачи.
Как расставить 6 стульев у 4 стен, чтобы
у каждой стены было по 2 стула.
Папа с двумя сыновьями отправился в поход. На их пути встретилась река. У берега плот. Он выдерживает на воде одного папу или двух сыновей. Как переправиться на другой берег папе с сыновьями?
Для одной лошади и двух коров выдают ежедневно 34 кг сена, а для двух лошадей и одной коровы -35кг сена. Сколько сена выдают ежедневно одной лошади и сколько одной корове?
Четыре утенка и пять гусят весят 4кг100г, а пять утят и четыре гусенка весят 4кг. Сколько весят один утенок?
Папа с двумя сыновьями отправился в поход. На их пути встретилась река. У берега плот. Он выдерживает на воде одного папу или двух сыновей. Как переправиться на другой берег папе с сыновьями?
Для одной лошади и двух коров выдают ежедневно 34 кг сена, а для двух лошадей и одной коровы -35кг сена. Сколько сена выдают ежедневно одной лошади и сколько одной корове?
Четыре утенка и пять гусят весят 4кг100г, а пять утят и четыре гусенка весят 4кг. Сколько весят один утенок?
Слайд 43 тип. Геометрические задачи.
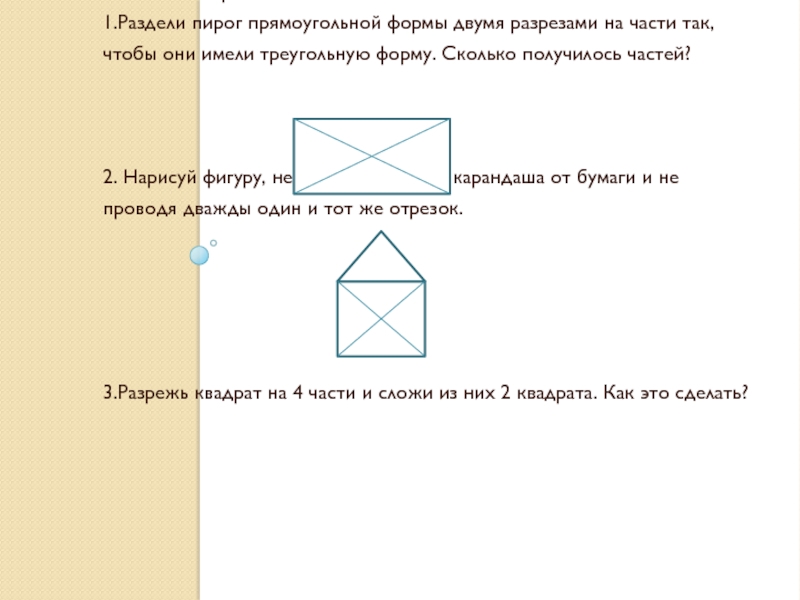
1.Раздели пирог прямоугольной формы двумя разрезами на части
так, чтобы они имели треугольную форму. Сколько получилось частей?
2. Нарисуй фигуру, не отрывая кончика карандаша от бумаги и не проводя дважды один и тот же отрезок.
3.Разрежь квадрат на 4 части и сложи из них 2 квадрата. Как это сделать?
2. Нарисуй фигуру, не отрывая кончика карандаша от бумаги и не проводя дважды один и тот же отрезок.
3.Разрежь квадрат на 4 части и сложи из них 2 квадрата. Как это сделать?
Слайд 52 тип. Логические квадраты.
1.Заполни квадрат (4 х 4) числами 1, 2,
3, 6 так, чтобы сумма чисел по всем строкам, столбцами и диагоналям была одинаковой. Числа в строках, столбцах и диагоналях не должны повторяться.
2.В квадрате нужно разместить еще числа 2,2,2,3,3,3 так, чтобы по всем линиям получить в сумме число 6.
2.В квадрате нужно разместить еще числа 2,2,2,3,3,3 так, чтобы по всем линиям получить в сумме число 6.
1
11
11
11,
Слайд 65 тип. Комбинаторные задачи.
1.У Даши 2 юбки: красная и синяя, и
2 блузки: в полоску и в горошек. Сколько разных нарядов у Даши?
2.Сколько существует двузначных чисел, у которых все цифры нечетные?
3. Родители приобрели путевку в Грецию. До Греции можно добраться, используя один из трех видов транспорта: самолет, теплоход или автобус. Составьте все возможные варианты использования данных видов транспорта.
4.Сколько разных слов можно образовать при помощи букв слова «соединение»?
2.Сколько существует двузначных чисел, у которых все цифры нечетные?
3. Родители приобрели путевку в Грецию. До Греции можно добраться, используя один из трех видов транспорта: самолет, теплоход или автобус. Составьте все возможные варианты использования данных видов транспорта.
4.Сколько разных слов можно образовать при помощи букв слова «соединение»?
Слайд 76 тип. Задачи на переливание.
1. Можно ли, имея лишь два сосуда
емкостью 3 и 5л, набрать из водопроводного крана 4 л воды?
2. Как разделить поровну между двумя семьями 12 л хлебного кваса, находящегося в двенадцатилитровом сосуде, воспользовавшись для этого двумя пустыми сосудами: восьмилитровым и трехлитровым?
3.Как, имея два сосуда емкостью 9л и 5л, набрать из водоема ровно 3 литра воды?
4.Бидон, емкость которого 10 литров, наполнен соком. Имеются еще пустые сосуды в 7 и 2 литров. Как разлить сок в два сосуда по 5 литров каждый?
2. Как разделить поровну между двумя семьями 12 л хлебного кваса, находящегося в двенадцатилитровом сосуде, воспользовавшись для этого двумя пустыми сосудами: восьмилитровым и трехлитровым?
3.Как, имея два сосуда емкостью 9л и 5л, набрать из водоема ровно 3 литра воды?
4.Бидон, емкость которого 10 литров, наполнен соком. Имеются еще пустые сосуды в 7 и 2 литров. Как разлить сок в два сосуда по 5 литров каждый?
Слайд 81.сведение путем преобразований нестандартной задачи к другой, ей сходной, но уже
стандартной задаче;
2. разбиение нестандартной задачи на несколько стандартных подзадач.
Для сведения нестандартной задачи к стандартной не существует определенных правил. Однако если внимательно, вдумчиво анализировать, решать каждую задачу, фиксируя в своей памяти все приемы, с помощью которых были найдены решения, какими методами были решены задачи, то вырабатывается умение в таком сведении.
2. разбиение нестандартной задачи на несколько стандартных подзадач.
Для сведения нестандартной задачи к стандартной не существует определенных правил. Однако если внимательно, вдумчиво анализировать, решать каждую задачу, фиксируя в своей памяти все приемы, с помощью которых были найдены решения, какими методами были решены задачи, то вырабатывается умение в таком сведении.
Процесс решения задачи
Слайд 9Пример
Рассмотрим на примере задачи:
По тропинке, вдоль кустов, шел десяточек хвостов,
Сосчитать
я также смог, что шагало тридцать ног.
Это вместе шли куда – то петухи и поросята.
Ну а мой вопрос таков – сколько было петухов?
И узнать я был бы рад - сколько было поросят?
Если не удается решить данную задачу, попытаемся свести ее к сходной.
В данной задаче можно применить принцип уравнивания.
Пусть все поросята встанут на задние ноги.
10*2 =20 столько ног шагает по тропинке
30 – 20 =10 столько передних ног у поросят
10:2 = 5 поросенка шло по тропинке
Ну а петушков 10 -5 =5.
Это вместе шли куда – то петухи и поросята.
Ну а мой вопрос таков – сколько было петухов?
И узнать я был бы рад - сколько было поросят?
Если не удается решить данную задачу, попытаемся свести ее к сходной.
В данной задаче можно применить принцип уравнивания.
Пусть все поросята встанут на задние ноги.
10*2 =20 столько ног шагает по тропинке
30 – 20 =10 столько передних ног у поросят
10:2 = 5 поросенка шло по тропинке
Ну а петушков 10 -5 =5.
Слайд 10Правила
1.«Простое» правило: не пропустите самую простую задачу.
Обычно простую задачу
не замечают. А начинать надо именно с неё.
2.«Очередное» правило: условия по возможности надо менять по очереди. Количество условий - конечное число, так что до всех рано или поздно дойдет очередь.
3. «Неизвестное» правило: изменив одно условие, другое, связанное с ним обозначьте х, а потом подберите его так, чтобы вспомогательная задача решалась при данном значении и не решалась при увеличении х на единицу.
4.«Интересное » правило: делайте условия задачи более интересными.
5. «Временное» правило: если в задаче идет какой-то процесс и конечное состояние более определенно, чем начальное, стоит запустить время в обратную сторону: рассмотреть последний шаг процесса, потом предпоследний и т.д.
2.«Очередное» правило: условия по возможности надо менять по очереди. Количество условий - конечное число, так что до всех рано или поздно дойдет очередь.
3. «Неизвестное» правило: изменив одно условие, другое, связанное с ним обозначьте х, а потом подберите его так, чтобы вспомогательная задача решалась при данном значении и не решалась при увеличении х на единицу.
4.«Интересное » правило: делайте условия задачи более интересными.
5. «Временное» правило: если в задаче идет какой-то процесс и конечное состояние более определенно, чем начальное, стоит запустить время в обратную сторону: рассмотреть последний шаг процесса, потом предпоследний и т.д.
Слайд 11пример
Задача №3.
У моста через речку встретились лодырь и черт. Лодырь пожаловался
на свою бедность. В ответ черт предложил:
- Я могу помочь тебе. Каждый раз, как ты перейдешь этот мост, у тебя деньги удвоятся. Но каждый раз, перейдя мост, ты должен будешь отдать мне 24 копейки. Три раза переходил мост лодырь, а когда заглянул в кошелек, там стало пусто. Сколько денег было у лодыря?
(((0+24):2+24):2+24):2= 21
При решении задач № 2и № 3 использовали «временное» правило.
- Я могу помочь тебе. Каждый раз, как ты перейдешь этот мост, у тебя деньги удвоятся. Но каждый раз, перейдя мост, ты должен будешь отдать мне 24 копейки. Три раза переходил мост лодырь, а когда заглянул в кошелек, там стало пусто. Сколько денег было у лодыря?
(((0+24):2+24):2+24):2= 21
При решении задач № 2и № 3 использовали «временное» правило.
Слайд 12Методика формирования умения решать нестандартные задачи.
Задача№1.
- По пустыне медленно идет
караван верблюдов, всего их 40. Если пересчитать все горбы у этих верблюдов, то получится 57 горбов. Сколько в этом караване одногорбых верблюдов?
- Сколько горбов может быть у верблюдов?
(их может быть два или один)
Давайте каждому верблюду на один горб прикрепим цветок.
- Сколько цветков потребуется? (40 верблюдов – 40 цветов)
- Сколько верблюдов останется без цветов?
( Таких будет 57-40=17. Это вторые горбы двугорбых верблюдов ).
- Сколько двугорбых верблюдов? (17)
- Сколько одногорбых верблюдов? (40-17=23)
- Каков же ответ задачи? (17 и 23 верблюдов).
- Сколько горбов может быть у верблюдов?
(их может быть два или один)
Давайте каждому верблюду на один горб прикрепим цветок.
- Сколько цветков потребуется? (40 верблюдов – 40 цветов)
- Сколько верблюдов останется без цветов?
( Таких будет 57-40=17. Это вторые горбы двугорбых верблюдов ).
- Сколько двугорбых верблюдов? (17)
- Сколько одногорбых верблюдов? (40-17=23)
- Каков же ответ задачи? (17 и 23 верблюдов).
Слайд 13Задача № 2.
-В гараже стояли легковые машины и мотоциклы
с колясками, всех вместе 18. У машин и мотоциклов – 65 колес. Сколько мотоциклов с колясками стояло в гараже, если у машин 4 колеса, а у мотоцикла – 3 колеса?
Переформулируем задачу. Грабители, пришедшие в гараж, где стояли 18 машин и мотоциклов с колясками, сняли с каждой машины и каждого мотоцикла по три колеса и унесли. Сколько колес осталось в гараже, если их было 65? Машине или мотоциклу они принадлежат?
- Сколько колес унесли грабители? (3*18=54колес)
- Сколько осталось колес? (65-54=11)
- Сколько машин было в гараже?
Или
-В гараже стояли 18 легковых машин и мотоциклов с коляской. У машин и мотоциклов 65 колес. Сколько в гараже мотоциклов, если в каждую коляску положили запасное колесо?
- Сколько стало колес у машин и мотоциклов вместе? (4*18=72)
- Сколько запасных колес положили в каждую коляску? (72-65= 7)
- Сколько машин в гараже? (18-7=11)
Переформулируем задачу. Грабители, пришедшие в гараж, где стояли 18 машин и мотоциклов с колясками, сняли с каждой машины и каждого мотоцикла по три колеса и унесли. Сколько колес осталось в гараже, если их было 65? Машине или мотоциклу они принадлежат?
- Сколько колес унесли грабители? (3*18=54колес)
- Сколько осталось колес? (65-54=11)
- Сколько машин было в гараже?
Или
-В гараже стояли 18 легковых машин и мотоциклов с коляской. У машин и мотоциклов 65 колес. Сколько в гараже мотоциклов, если в каждую коляску положили запасное колесо?
- Сколько стало колес у машин и мотоциклов вместе? (4*18=72)
- Сколько запасных колес положили в каждую коляску? (72-65= 7)
- Сколько машин в гараже? (18-7=11)