Методическая разработка
Градович Н.А.,
учителя математики
ГОКУ ШКОЛА-ИНТЕРНАТ № 8
Г. ИРКУТСК
2017г.
- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по математикеИгровые методы
Содержание
- 1. Презентация по математикеИгровые методы
- 2. Главная сила математики состоит в том, что
- 3. Задачи: ознакомиться с методикой использования занимательных заданий
- 4. Характерные признаки занимательных задачтакая задача (как
- 5. Классификации и типологизации задач, применяемых в учебном процессе
- 6. Стандартные прикладные задачиЗадачи с лишними, недостающими или
- 7. Примеры:. На столе лежат линейка, карандаш, циркуль
- 8. Что не может увеличить лупа в треугольнике?
- 9. Классификация нестандартных задач, не являющихся прикладными
- 10. проведение и использование аналогий, определение различий заданных
- 11. Примеры:За столом сидят ковбой, джентльмен и йог.
- 12. Марина мечтала о шоколадке, но ей на
- 13. Слайд 13
- 14. Слайд 14
- 15. Слайд 15
- 16. Задачи-рисунки1. Сколько туристов живет в этом лагере?2.
- 17. ИГРОВЫЕ ТЕХНОЛОГИИ КАК ФОРМА ПРЕДЪЯВЛЕНИЯ И РЕШЕНИЯ ЗАНИМАТЕЛЬНЫХ ЗАДАЧ НА УРОКАХ МАТЕМАТИКИ
- 18. Слайд 18
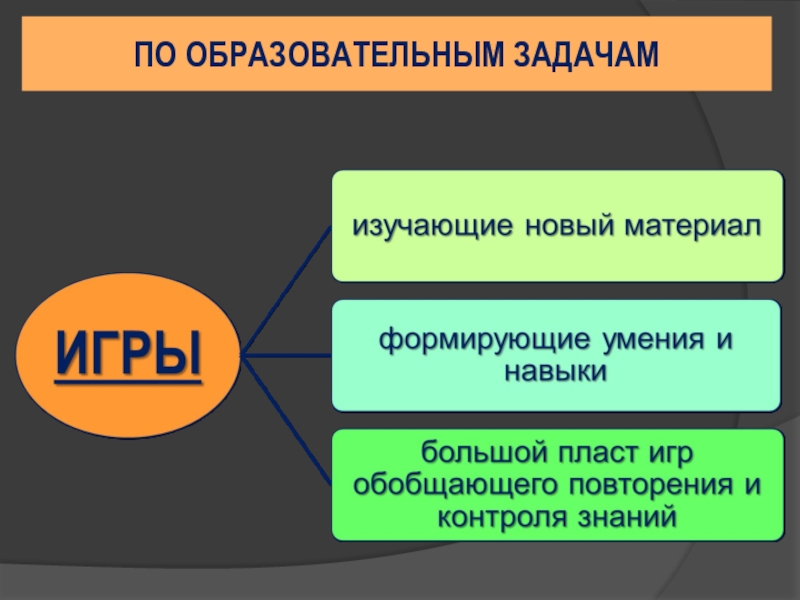
- 19. ПО ОБРАЗОВАТЕЛЬНЫМ ЗАДАЧАМ
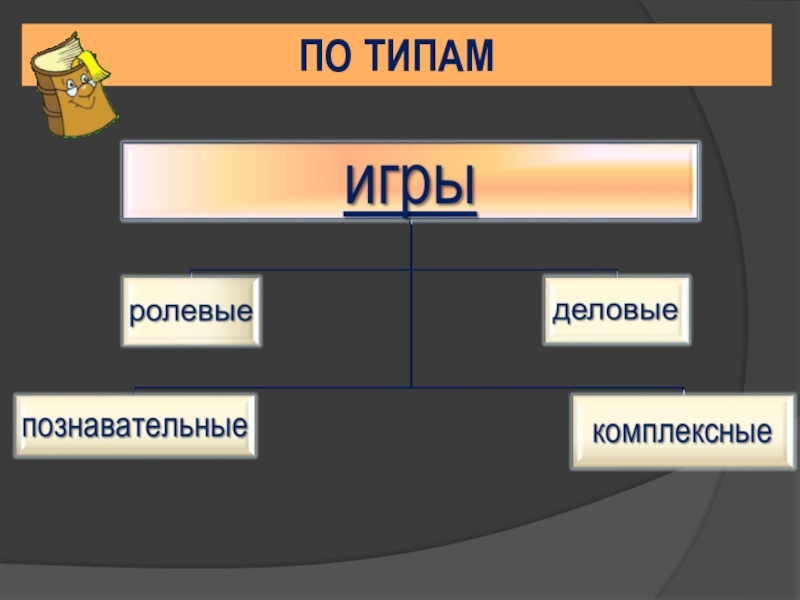
- 20. ПО ТИПАМ
- 21. ПО ФОРМЕ ПРОВЕДЕНИЯигры – аукционызащитысоревнования на лучшее
- 22. КОЛЛЕКТИВНЫЕ ИГРЫ
- 23. Основные структурные компоненты дидактической игры
- 24. Вопросы методики при организации дидактических игрцель
- 25. Результативность включения занимательных задач с использованием
- 26. Игра “Домино”. Правила игры: Для игры готовятся
- 27. Слайд 27
- 28. Слайд 28
- 29. «Без игры не может быть
- 30. Спасибо за внимание!!!!
Главная сила математики состоит в том, что вместе с решением одной конкретной задачи она создаёт общие приёмы и способы, применимые во многих ситуациях, которые даже не всегда можно предвидеть.
Слайд 1ИСПОЛЬЗОВАНИЕ ИГРОВЫХ МЕТОДОВ НА УРОКАХ МАТЕМАТИКИ В ШКОЛЕ ДЛЯ ДЕТЕЙ С
НАРУШЕНИЯМИ ЗРЕНИЯ»
Слайд 2Главная сила математики состоит в том, что вместе с решением одной
конкретной задачи она создаёт общие приёмы и способы, применимые во многих ситуациях, которые даже не всегда можно предвидеть.
М.Башмаков
М.Башмаков
Слайд 3
Задачи:
ознакомиться с методикой использования занимательных заданий на уроке математики
изучить
приемы составления занимательных заданий
изучить использование занимательных задач в игровых технологиях
изучить использование занимательных задач в игровых технологиях
Цель: расширение и систематизация знаний методики применения занимательных задач на уроках математики с применением игровых технологий
Слайд 4Характерные признаки
занимательных задач
такая задача (как и любая задача вообще) имеет
развивающую направленность
в задаче должны быть использованы нестандартные формы и способы представления данных
в качестве исходных данных и ситуаций используются вымышленные или реальные персонажи, оперируя которыми требуется достигнуть заданной цели
это качественная задача, решение которой строится на рассуждении без применения математических выкладок
задача включает в себя необычно поставленный вопрос
в задаче должны быть использованы нестандартные формы и способы представления данных
в качестве исходных данных и ситуаций используются вымышленные или реальные персонажи, оперируя которыми требуется достигнуть заданной цели
это качественная задача, решение которой строится на рассуждении без применения математических выкладок
задача включает в себя необычно поставленный вопрос
Слайд 6Стандартные прикладные задачи
Задачи с лишними, недостающими или противоречивыми данными
Задачи без явной
постановки вопроса или с неявной его постановкой
Задачи с нестандартной формой изложения данных (рисунок, схема, диаграмма)
Задачи с реккурентным способом постановки данных и условий
Задачи, направленные на установление взаимосвязи, проведения аналогии, обобщения
Задачи имеющие нестандартную фабулу постановки и задания вопроса
Задачи в форме игр либо заданий практической работы
Задачи данные в которых представлены в непривычных (нестандартных) единицах измерения
Задания на нахождение ошибок, подтверждение истинности или обнаружение смысловых противоречий
Задачи с нестандартной формой изложения данных (рисунок, схема, диаграмма)
Задачи с реккурентным способом постановки данных и условий
Задачи, направленные на установление взаимосвязи, проведения аналогии, обобщения
Задачи имеющие нестандартную фабулу постановки и задания вопроса
Задачи в форме игр либо заданий практической работы
Задачи данные в которых представлены в непривычных (нестандартных) единицах измерения
Задания на нахождение ошибок, подтверждение истинности или обнаружение смысловых противоречий
Слайд 7Примеры:
. На столе лежат линейка, карандаш, циркуль и резинка. На листе
бумаги нужно начертить окружность. С чего Вы начнете?
Ответ: Надо достать лист бумаги.
Шли два отца и два сына. Нашли три апельсина. Не резали, не пилили, а поровну разделили. Как это может быть? Ответ: это были дед, отец и сын.
Шли два отца и два сына. Нашли три апельсина. Не резали, не пилили, а поровну разделили. Как это может быть? Ответ: это были дед, отец и сын.
Слайд 8Что не может увеличить лупа в треугольнике?
Ответ: Углы
В каком числе цифр столько,
сколько букв в его названии?
Ответ: 100 (сто), 1000000 (миллион)
Два человека играли в шашки. Каждый сыграл по пять партий и выиграл по пять раз. Как это возможно? Ответ: Оба человека играли с другими людьми.
Два человека играли в шашки. Каждый сыграл по пять партий и выиграл по пять раз. Как это возможно? Ответ: Оба человека играли с другими людьми.
Слайд 10проведение и использование аналогий, определение различий заданных объектов, процессов или явлений,
установление противоположности заданных явлений и процессов или их антиподов;
осуществление практической демонстрации, абстрагирование от тех или иных свойств объекта, процесса, явления или конкретизации той или иной стороны данного явления;
установка причинно-следственных отношений между заданными объектами, процессами или явлениями;
построение аналитическим или синтетическим путем причинно-следственных цепочек с последующим анализом получившихся вариантов;
правильное осуществление последовательности определенных действий, избегая ошибок-«ловушек»;
осуществление перехода от плоскостного к пространственному варианту заданного процесса, объекта, явления или наоборот
осуществление практической демонстрации, абстрагирование от тех или иных свойств объекта, процесса, явления или конкретизации той или иной стороны данного явления;
установка причинно-следственных отношений между заданными объектами, процессами или явлениями;
построение аналитическим или синтетическим путем причинно-следственных цепочек с последующим анализом получившихся вариантов;
правильное осуществление последовательности определенных действий, избегая ошибок-«ловушек»;
осуществление перехода от плоскостного к пространственному варианту заданного процесса, объекта, явления или наоборот
Слайд 11Примеры:
За столом сидят ковбой, джентльмен и йог. Сколько ног стоит на
полу?
Ответ: 1 нога (ковбой кладет ноги на стол, джентльмен кладет ногу на ногу,а йог медитирует)
Слайд 12Марина мечтала о шоколадке, но ей на покупку не хватало 10
рублей. Вася тоже мечтал о шоколадке, но ему не доставало всего 1 рубля. Дети решили купить хотя бы одну шоколадку на двоих, но им все равно не хватило 1 рубля. Какова стоимость шоколадки?
Ответ: Стоимость - 10 рублей. У Марины нет денег вообще.
Слайд 16Задачи-рисунки
1. Сколько туристов живет в этом лагере?
2. Когда они сюда приехали:
сегодня или несколько дней назад?
3. На чем они сюда приехали?
4. Далеко ли от лагеря до ближайшего селения?
5. Откуда дует ветер: с севера или юга?
6. Какое сейчас время дня? 7. Куда ушел Шура? 8. Кто вчера был дежурным (назовите по имени)? 9. Какое сегодня число какого месяца?
3. На чем они сюда приехали?
4. Далеко ли от лагеря до ближайшего селения?
5. Откуда дует ветер: с севера или юга?
6. Какое сейчас время дня? 7. Куда ушел Шура? 8. Кто вчера был дежурным (назовите по имени)? 9. Какое сегодня число какого месяца?
Слайд 17ИГРОВЫЕ ТЕХНОЛОГИИ КАК ФОРМА ПРЕДЪЯВЛЕНИЯ И РЕШЕНИЯ ЗАНИМАТЕЛЬНЫХ ЗАДАЧ НА УРОКАХ
МАТЕМАТИКИ
Слайд 21ПО ФОРМЕ ПРОВЕДЕНИЯ
игры – аукционы
защиты
соревнования на лучшее качество, скорость, количество
путешествие
по станциям с чередованием игровых ситуаций
имитация событий
пресс – конференция
игры – драматизации
инсценировки
поиск решения проблем
игры - исследования, открытия
имитация событий
пресс – конференция
игры – драматизации
инсценировки
поиск решения проблем
игры - исследования, открытия
Слайд 24Вопросы методики
при организации дидактических игр
цель игры
количество играющих
какие дидактические материалы и
пособия понадобятся для игры?
как с наименьшей затратой времени познакомить ребят с правилами игры?
на какое время должна быть рассчитана игра? Будет ли она занимательной, захватывающей? Пожелают ли ученики вернуться к ней ещё раз?
как обеспечить участие всех школьников в игре?
как организовать наблюдение за детьми, чтобы выяснить, все ли включились в работу?
какие изменения можно внести в игру, чтобы повысить интерес и активность детей?
какие выводы следует сообщить учащимся в заключение, после игры
как с наименьшей затратой времени познакомить ребят с правилами игры?
на какое время должна быть рассчитана игра? Будет ли она занимательной, захватывающей? Пожелают ли ученики вернуться к ней ещё раз?
как обеспечить участие всех школьников в игре?
как организовать наблюдение за детьми, чтобы выяснить, все ли включились в работу?
какие изменения можно внести в игру, чтобы повысить интерес и активность детей?
какие выводы следует сообщить учащимся в заключение, после игры
Слайд 25Результативность включения занимательных задач
с использованием игровых технологий
Дети используют знания, умения
и навыки, полученные на уроках математики, в практической деятельности.
Формируются навыки, позволяющие продолжить обучение в техникуме, ПТУ или профильном классе.
Дети осваивают коммуникативный, аналитический, проектировочный, творческий типы деятельности.
Учащиеся овладевают математическими знаниями, умениями и навыками разного уровня сложности: от минимальных, соответствующих обязательным результатам обучения, до повышенных, позволяющих продолжить обучение в математическом, физическом классах, а также в классах с углубленным изучением информатики
У учащихся формируется представление о математике как о предмете, где каждому есть возможность выразиться.
Приобретается навык работы со справочной литературой, проводятся необходимые измерения, подбираются доступные приборы, анализируются полученные результаты. У учащихся формируется представление о математике как о предмете, где каждому есть возможность выразиться.
Учащиеся адекватно оценивают деятельность одноклассников (с помощью консультантов).
Изменяется поведение детей в коллективе: они начинают прислушиваться к мнению других, без боязни высказывают свое собственное мнение.
Формируются навыки, позволяющие продолжить обучение в техникуме, ПТУ или профильном классе.
Дети осваивают коммуникативный, аналитический, проектировочный, творческий типы деятельности.
Учащиеся овладевают математическими знаниями, умениями и навыками разного уровня сложности: от минимальных, соответствующих обязательным результатам обучения, до повышенных, позволяющих продолжить обучение в математическом, физическом классах, а также в классах с углубленным изучением информатики
У учащихся формируется представление о математике как о предмете, где каждому есть возможность выразиться.
Приобретается навык работы со справочной литературой, проводятся необходимые измерения, подбираются доступные приборы, анализируются полученные результаты. У учащихся формируется представление о математике как о предмете, где каждому есть возможность выразиться.
Учащиеся адекватно оценивают деятельность одноклассников (с помощью консультантов).
Изменяется поведение детей в коллективе: они начинают прислушиваться к мнению других, без боязни высказывают свое собственное мнение.
Слайд 26Игра “Домино”.
Правила игры:
Для игры готовятся карточки с дифференцированными заданиями,
чтобы в игре могли участвовать все ребята. Каждая карточка делится на две части. В этих частях размещают задания и ответы. Карточки раздают участникам игры. Играющие по очереди выставляют свои карточки так, как в обычном домино, чтобы в конце игры цепочка замкнулась, но чтобы каждая следующая карточка была логически связана с предыдущей. При этом необходимо теоретически обосновать тот факт, который написан на карточке игрока. Если ученик неправильно выставил карточку или не сумел объяснить причину ее выставления, то он может воспользоваться помощью ребят, но за это ему снижается оценка.
Игра проводится на уроке как один из этапов групповой работы для повторения и закрепления материала по всей пройденной теме или нескольким темам. Предполагается наличие нескольких комплектов игры, чтобы активизировать работу учащихся. В каждой группе обязательно наличие арбитра, который будет оценивать правильность ответа. Ими могут быть наиболее успевающие учащиеся класса или старшеклассники.
Игра проводится на уроке как один из этапов групповой работы для повторения и закрепления материала по всей пройденной теме или нескольким темам. Предполагается наличие нескольких комплектов игры, чтобы активизировать работу учащихся. В каждой группе обязательно наличие арбитра, который будет оценивать правильность ответа. Ими могут быть наиболее успевающие учащиеся класса или старшеклассники.
Слайд 29 «Без игры не может быть полноценного умственного развития. Игра
- это огромное светлое окно, через которое в духовный мир ребёнка вливается живительный поток представлений, понятий. Игра - это искра, зажигающая огонёк пытливости и любознательности.»
В.А.Сухомлинский
В.А.Сухомлинский