- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по математике Задачи с практическим содержанием по теме Арифметическая и геометрическая прогрессия
Содержание
- 1. Презентация по математике Задачи с практическим содержанием по теме Арифметическая и геометрическая прогрессия
- 2. Содержание:Арифметическая прогрессияТеория.Задачи для самостоятельного решения.Геометрическая прогрессияТеория.Задачи для самостоятельного решения.Занимательные задачи на применение формул прогрессий.
- 3. Арифметическая прогрессия:Арифметической прогрессией называется ряд чисел, в
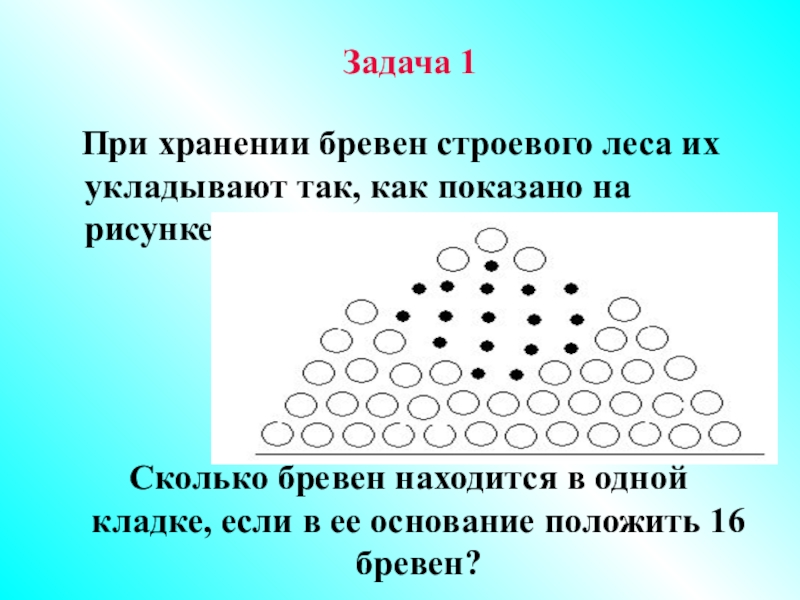
- 4. Задача 1
- 5. Задача 1 При хранении бревен строевого
- 6. Задача 2: Диаметры пяти шкивов, насаженных на
- 7. Задача 3: За первый день было вспахано
- 8. Задача 4: Два тела, находясь на расстоянии
- 9. Задачи для самостоятельного решения:За изготовление и установку
- 10. Геометрическая прогрессия:Геометрическая прогрессия - это ряд чисел,
- 11. Задача 1: Известно, что бактерия в питательной
- 12. Задача 2: После каждого качания поршня под
- 13. Задача 3 В сберегательный банк внесли вклад
- 14. Служившему воину дано вознаграждение за 1 рану
- 15. Пусть число ран n, то 1+2+4+8+…+2n-1=65535.
- 16. Решение: 80*(1+81+812+813+814+…+819)+1Выражение в скобках
- 17. у = Решение: Область определения функции: х
- 18. График функции выглядит так:
- 19. Занимательные задачи на применение формул прогрессийОднажды богач
- 20. "Прогрессио - движение вперёд!"Урок сегодня завершён,
Слайд 1ЗАДАЧИ С ПРАКТИЧЕСКИМ СОДЕРЖАНИЕМ ПО ТЕМЕ:
«АРИФМЕТИЧЕСКАЯ И ГЕОМЕТРИЧЕСКАЯ ПРОГРЕССИИ»
Слайд 2Содержание:
Арифметическая прогрессия
Теория.
Задачи для самостоятельного решения.
Геометрическая прогрессия
Теория.
Задачи для самостоятельного решения.
Занимательные задачи на
Слайд 3Арифметическая прогрессия:
Арифметической прогрессией называется ряд чисел, в котором каждое число, начиная
Формула п - го члена: ап= а1+ d(п-1)
d- разность арифметической прогрессии: d= ап+1 - ап
Характеристическое свойство: ап = (ап-1 + ап+1 ): 2
Формулы суммы п- первых членов:
Слайд 4 Задача 1
Представь, что ты прораб
Слайд 5Задача 1
При хранении бревен строевого леса их укладывают так,
Сколько бревен находится в одной кладке, если в ее основание положить 16 бревен?
Слайд 6Задача 2: Диаметры пяти шкивов, насаженных на общий вал, образуют арифметическую
Решение: По условию задачи а1 + а3 = 268; а2 + а4 = 316, найти требуется а1, а2, а3, а4, а5
Составим и решим систему уравнений, используя формулу
ап = а1+ d(п-1)
Подставив полученные значения в формулу ап = а1+ d(п-1), найдем остальные значения
а2 = 134, а3 = 158, а4 = 182, а5 = 206
Ответ: 110, 134, 158, 182, 206
Слайд 7Задача 3: За первый день было вспахано 100 га пашни, а
Решение: По условию задачи а1 = 100, d = 3, n = 19, значит найти требуется S19.
По формуле:
Ответ: 2413
Слайд 8Задача 4: Два тела, находясь на расстоянии 153 м друг от
Решение: Первое тело движется равномерно, и поэтому путь, пройденный этим телом, вычисляется по формуле: S=V·t. Движение второго тела подчиняется законам арифметической прогрессии где а1 = 3, d = 5
Поэтому
необходимо найти t.
Из условия задачи получаем уравнение:
5t2 + 21t - 306 =0
t1=6, t2= -10,2
Второй корень не удовлетворяет условию t∈Ν
Ответ: 6
Слайд 9Задачи для самостоятельного решения:
За изготовление и установку первого железобетонного кольца заплатили
Ответ:1620
За рытье колодца оплачивается за первый метр глубины 150 уе., а за каждый следующий – на 10 уе. больше, чем за предыдущий. Вычислить стоимость работы, если глубина колодца составила 10 м. Ответ:1950
Шар, катящийся по желобу, в первую секунду проходит 0,6 м, а путь, пройденный в каждую следующую секунду, увеличивается на 0,6 м. Сколько секунд будет двигаться шар по шестиметровому желобу? Ответ:4
Турист, двигаясь по пересеченной местности, за первый час пути прошел 800 в, а за каждый следующий час проходил на 25 м меньше, чем за предыдущий. Сколько времени он потратил на путь, равный 5700 м? Ответ: 8
Слайд 10Геометрическая прогрессия:
Геометрическая прогрессия - это ряд чисел, каждое из которых получается
Формула п - го члена: bп= b1 ·qn1
q- знаменатель геометрической прогрессии:
q= bn+1 : bn
Характеристическое свойство:
Формулы суммы п - первых членов:
Слайд 11Задача 1: Известно, что бактерия в питательной среде через каждые полчаса
Решение: Бактерия была одна, следовательно, b1=1. Она делится на две, значит q=2, а так как время деления полчаса, то за 10 часов произойдет 20 делений и нам нужно найти b21
По формуле: bп= b1 ·qn1
b21 = 1·220 =1048576 ≈ 1,05·106
Ответ: 10,5·106
Слайд 12Задача 2: После каждого качания поршня под колоколом воздушного насоса давление
Решение: Из условия задачи получаем, что b1=760; q=0,83; n = 16, а найти необходимо b16 .
По формуле bп= b1 ·qn1 , значит:
b16=760 ·0,8315 ≈ 46,45
Ответ: 46,45
Слайд 13Задача 3 В сберегательный банк внесли вклад в размере 10000 рублей
Решение: За один год банк выплатит S1 = b1 + b1 q=b1 ·(1+q),
где b1- вклад, q- процентная ставка.
За 2 года S2 =S1+S1q = S1 (1+q), но S1=b1·(1+q), следовательно, S2=b1·(1+q)2.
Тогда за n лет Sn = b1·(1+q)n
Найдем по этой формуле S4 , S4 = b1·(1+q)4
10000·(1+2%:100%)4 = 10000 · 1,02 4 = 10824,32
10824 руб. 32 коп.
Ответ:10824,32
Слайд 14Служившему воину дано вознаграждение за 1 рану 1 копейка,
за
за третью – 4 копейки и т.д.
По исчислению нашлось, что воин получил вознаграждение 655 рублей 35 копеек. Спрашивается число его ран.
Занимательные задачи
№1 «Вознаграждение воина»
Слайд 15 Пусть число ран n, то
1+2+4+8+…+2n-1=65535.
1,2,4,8,… -геометрическая прогрессия, b1=1,
Sn=(1-2n-1*2)/(1-2)= 2n-1=65535.
2n=65536, 2n=216, n=16.
Ответ: воин имел 16 ран.
РЕШЕНИЕ
Слайд 16Решение:
80*(1+81+812+813+814+…+819)+1
Выражение в скобках
1,
b1=1, b2=81, q= 81, bn=819
Sn=(1-81*819)/(1-81)= (1-8110)/(-80)
(80* (1-8110)/(-80))+1=-1+8110+1=8110
№2 Вычислить
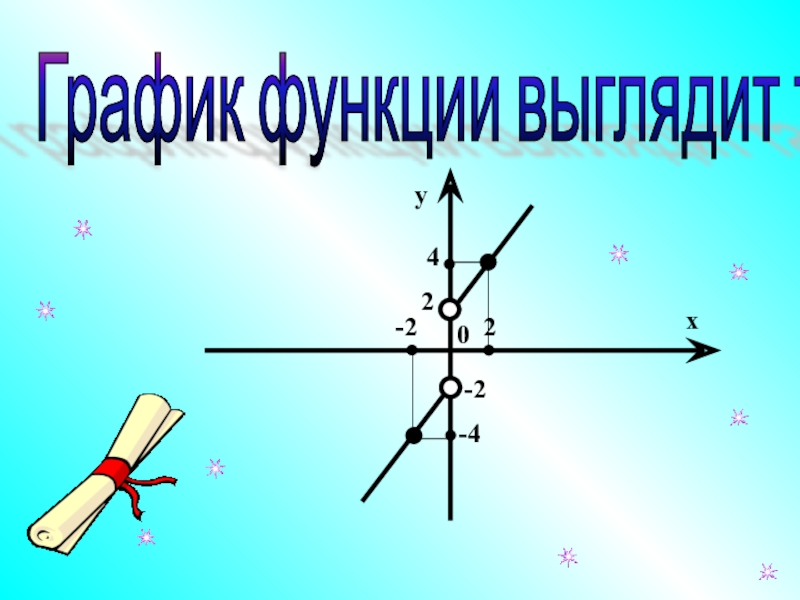
Слайд 17у =
Решение: Область определения функции: х ≠ 0.
1 +
Тогда S = 1 : (1 – 1/2 ) = 2.
Функция приобретает вид; 1) у = х + 2, если х > 0;
2) у = х – 2, если х < 0.
2
4
Задание №3 Построить график функции
Слайд 19Занимательные задачи на применение формул прогрессий
Однажды богач заключил выгодную, как ему
Ответ: получил 3·106 руб., отдал примерно 107 руб.,
богач проиграл
2. Больной принимает лекарство по следующей схеме: в первый день он принимает 5 капель, а в каждый следующий день – на 5 капель больше, чем в предыдущий. Дойдя до нормы 40 капель в день, он 3 дня пьёт по 40 капель, а потом ежедневно уменьшает прием на 5 капель, доведя его до 5 капель в последний день. Сколько пузырьков лекарства нужно купить больному, если в каждом содержится 20 мл лекарства (что составляет 200 капель)?
Ответ: 2 пузырька
3. Улитка ползет вверх по дереву, начиная от его основания. За первую минуту она проползла 30 см, а за каждую следующую минуту – на 5 см больше, чем за предыдущую. За какое время улитка достигнет вершины дерева высотой 5,25 м?
Ответ: 10 минут