- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по математике Задачи по теории вероятностей
Содержание
- 1. Презентация по математике Задачи по теории вероятностей
- 2. Запишите все трехзначные числа, для записи которых
- 3. Запишите все трехзначные числа, для записи которых употребляются только цифры 0 и 7.
- 4. 1. Запишите все трехзначные числа, в запись которых входят лишь цифры:
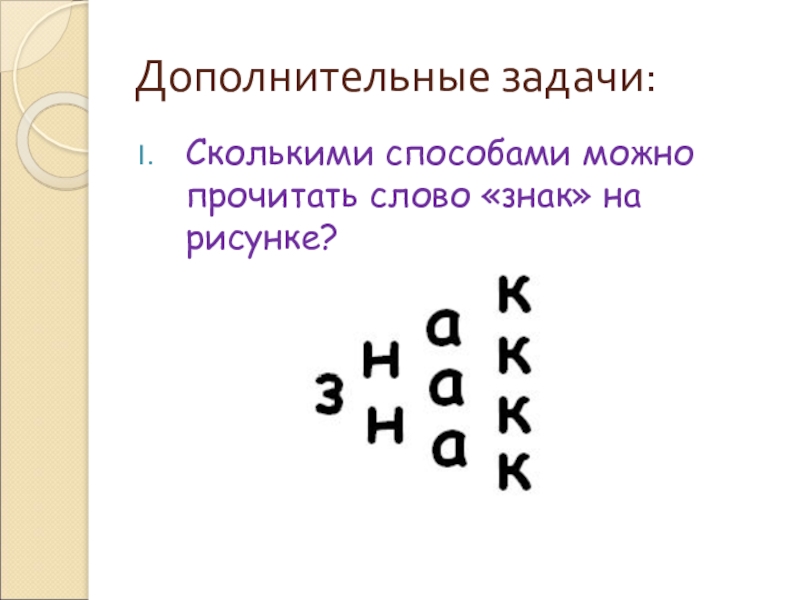
- 5. Дополнительные задачи:Сколькими способами можно прочитать слово «знак» на рисунке?
- 6. Сколько трехзначных чисел можно составить из цифр
- 7. 2. Сколько двузначных чисел можно составить так, чтобы в записи этих чисел не повторялись цифры:
- 8. В правление фирмы входят 5 человек. Из
- 9. 3. Сколькими способами можно выбрать капитана и вратаря для футбольной команды пятого класса, если в ней:
- 10. Семье, состоящей из бабушки, папы, мамы, дочери
- 11. Произведение нескольких последовательных натуральных чисел называют ФАКТОРИАЛОМ
- 12. 4. Вычислите:
- 13. Дополнительные задачи:2. Найдите значения выражений:а) 4! –
- 14. Дополнительные задачи:3. К полднику в детском саду
- 15. СПАСИБО ЗА УРОК!
Слайд 2Запишите все трехзначные числа, для записи которых употребляются только цифры 1
Решение. В записи числа на первом слева месте (в разряде сотен) может стоять цифра 1 или цифра 2:
или
На втором месте (в разряде десятков) в каждом случае также одна из двух цифр – 1 или 2:
На третьем месте (в разряде единиц) в каждом из полученных четырех случаев также можно записать либо 1, либо 2:
Получили 8 чисел: 111, 112, 121, 122, 211, 212, 221, 222.
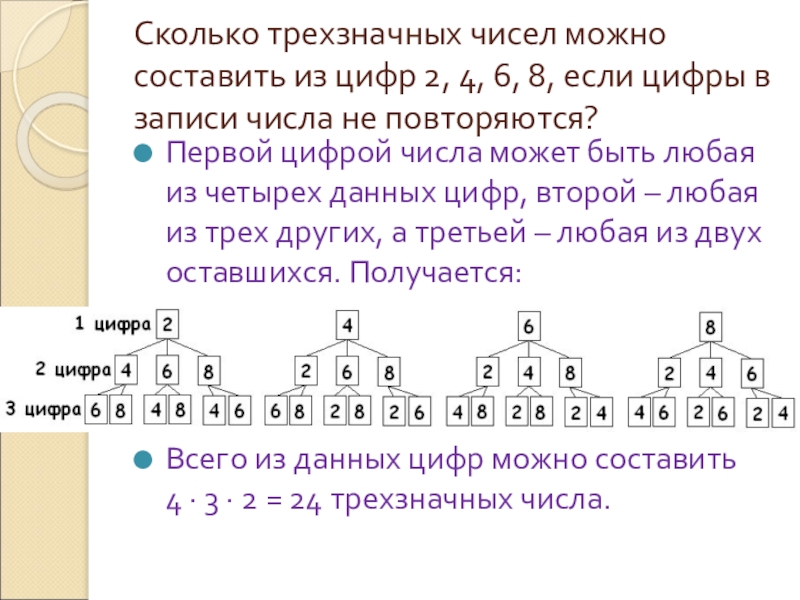
Слайд 6Сколько трехзначных чисел можно составить из цифр 2, 4, 6, 8,
Первой цифрой числа может быть любая из четырех данных цифр, второй – любая из трех других, а третьей – любая из двух оставшихся. Получается:
Всего из данных цифр можно составить 4 · 3 · 2 = 24 трехзначных числа.
Слайд 72. Сколько двузначных чисел можно составить так, чтобы в записи этих
Слайд 8В правление фирмы входят 5 человек. Из своего состава правление должно
Решение. Президентом фирмы можно избрать одного из 5 человек:
После того как президент избран, вице-президентом можно выбрать любого из четырех оставшихся членов правления:
Значит, выбрать президента можно пятью способами, и для каждого выбранного президента четырьмя способами можно выбрать вице-президента. Следовательно, общее число способов выбрать президента и вице-президента фирмы равно: 5 · 4 = 20 способов.
Слайд 93. Сколькими способами можно выбрать капитана и вратаря для футбольной команды
Слайд 10Семье, состоящей из бабушки, папы, мамы, дочери и сына, подарили 5
Решение. Бабушка может выбрать одну любую чашку из пяти, папа может выбрать любую чашку из четырех оставшихся, мама – из трех оставшихся, дочь – одну из двух оставшихся, а сын – только одну чашку. Каждому выбору одного человека соответствует некоторое количество выборов другого. Тогда количество всех выборов можно найти так:
5 · 4 · 3 · 2 · 1 = 120 способов разделить чашки.
Слайд 11Произведение нескольких последовательных натуральных чисел называют ФАКТОРИАЛОМ и обозначают знаком «!».
Например,
4! = 1 · 2 · 3 · 4 = 24.
3! = 1 · 2 · 3 = 6.
2! = 1 · 2 = 2.
1! = 1.
Кстати, считается, что 0! = 1.
В общем виде
n! = 1 · 2 · 3 · … · (n – 1) · n.