Выполнила: Харисова Азалия Рустемовна
ученица 5б класса МОБУ СОШ №1
Руководитель: Крылова Наталья Геннадьевна,
учитель математики МОБУ СОШ №1
- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад ПО МАТЕМАТИКЕ УМНОЖЕНИЕ С УВЛЕЧЕНИЕМ
Содержание
- 1. ПРЕЗЕНТАЦИЯ ПО МАТЕМАТИКЕ УМНОЖЕНИЕ С УВЛЕЧЕНИЕМ
- 2. исследовательская работа по математикеУмножение с увлечением. «Предмет математики
- 3. Цель моего исследования – изучить методы и
- 4. Гипотеза моего исследования: если показать, что применение
- 5. Нестандартные способы умножения.1. Индийский способ умножения.2. Умножение
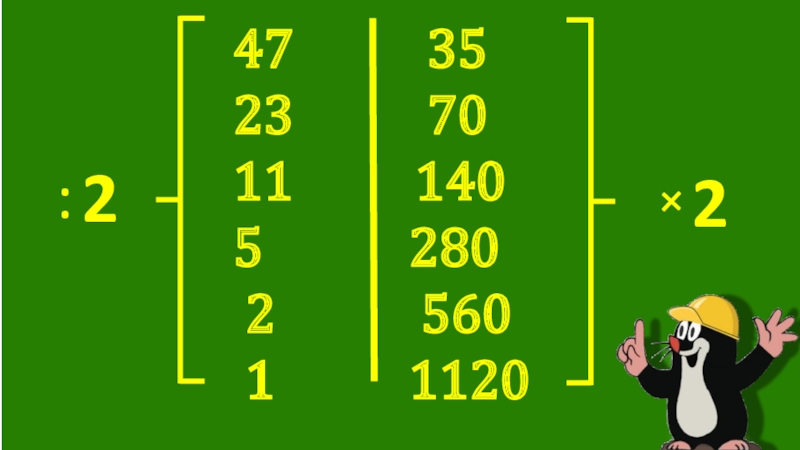
- 6. «Крестьянский способ»умножения
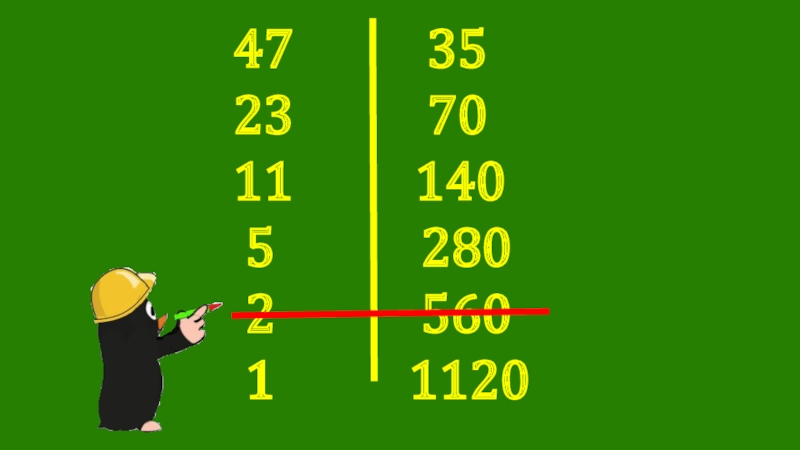
- 7. 47 3523
- 8. 47 3523
- 9. 35+70+140+280+1120=1645Итак, 47 35=1645+
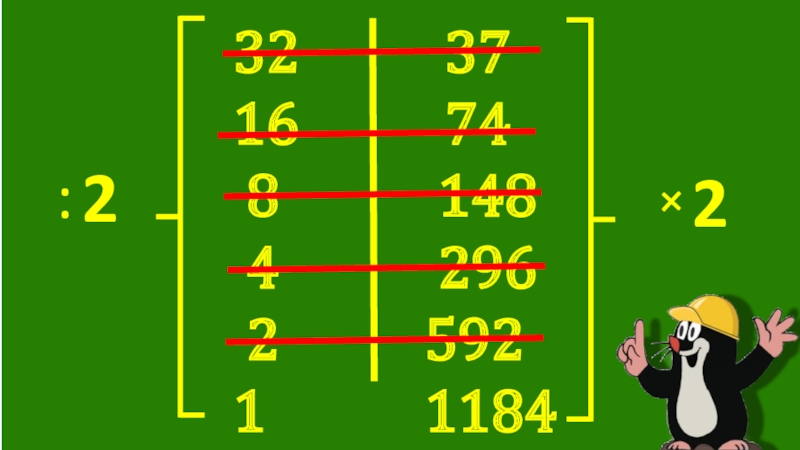
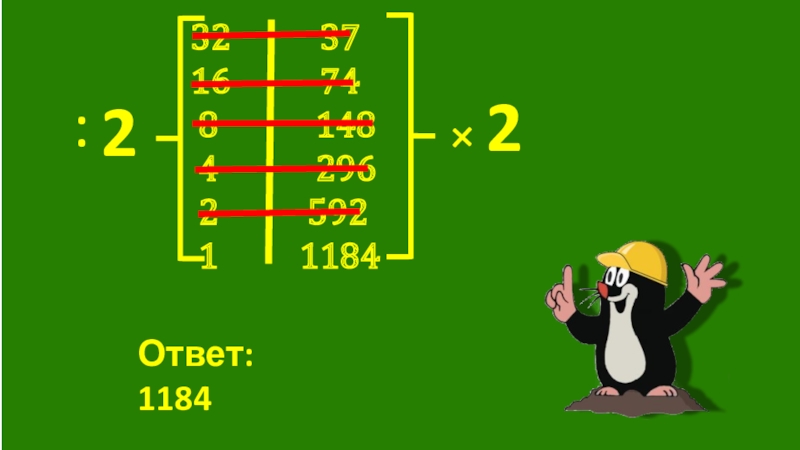
- 10. 32 3716
- 11. 32 3716
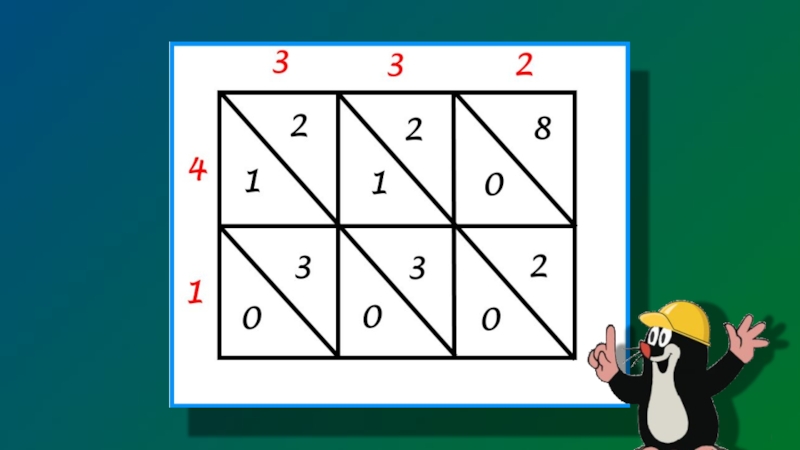
- 12. Способ описанныйАбу Абдалахом аль – Хорезмиили способ «Решетки»
- 13. Слайд 13
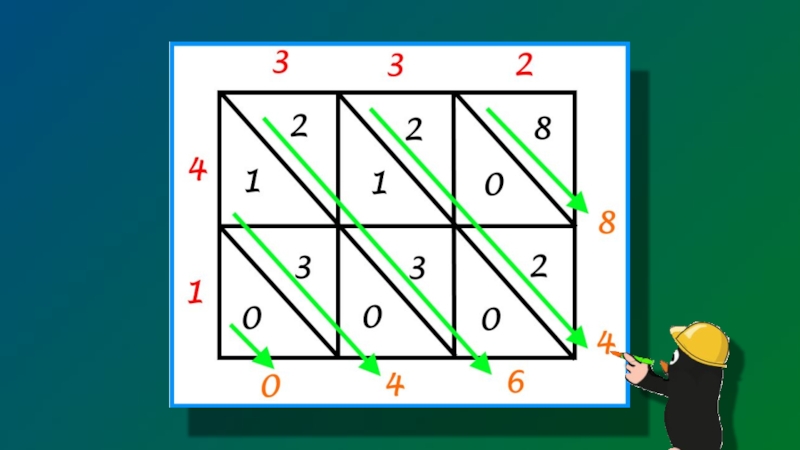
- 14. Слайд 14
- 15. Читаем получившиеся числа: 04648Ноль вначале отбрасываем -4648
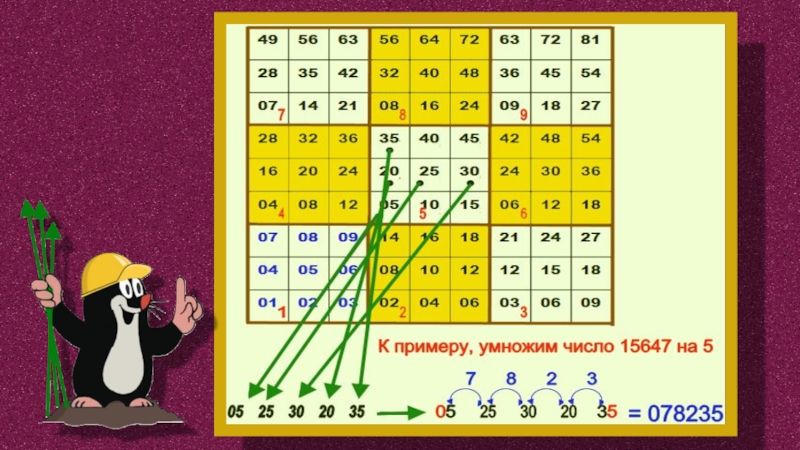
- 16. Способ умножения академика Оконешникова
- 17. Слайд 17
- 18. 1. Умножение на 11Умножение на
- 19. Мастер класс
- 20. Умножение на 11«Краешки сложи, в серединку положи»
- 21. Умножение на 22, 33, ..., 99Чтобы двузначное
- 22. Умножение двузначного числа на 101, 1001 и
- 23. Умножение чисел, близких к 100 и
- 24. Слайд 24
- 25. Слайд 25
- 26. Спасибо за внимание
исследовательская работа по математикеУмножение с увлечением. «Предмет математики настолько серьезен, что полезно не упускать случаев делать его немного занимательным».
Слайд 2
исследовательская работа по математике
Умножение с увлечением.
«Предмет математики настолько серьезен,
что
полезно не упускать случаев делать
его немного занимательным».
Б. Паскаль
Б. Паскаль
Слайд 3
Цель моего исследования – изучить методы и приёмы нестандартного умножения, которые
не только помогут вам во время покупок или при каких-либо расчётах, но вызовут немалое удивление у знакомых и товарищей, ведь свободное выполнение счётных операций в значительной степени может свидетельствовать о незаурядности вашего интеллекта.
Я поставила перед собой следующие задачи
1. изучить историю возникновения вычислений
2. рассмотреть правила вычислений, которыми пользовались в древности и которыми пользуются сейчас,
3. освоить правила быстрого счета и научить этому ребят нашего класса.
Я поставила перед собой следующие задачи
1. изучить историю возникновения вычислений
2. рассмотреть правила вычислений, которыми пользовались в древности и которыми пользуются сейчас,
3. освоить правила быстрого счета и научить этому ребят нашего класса.
Слайд 4
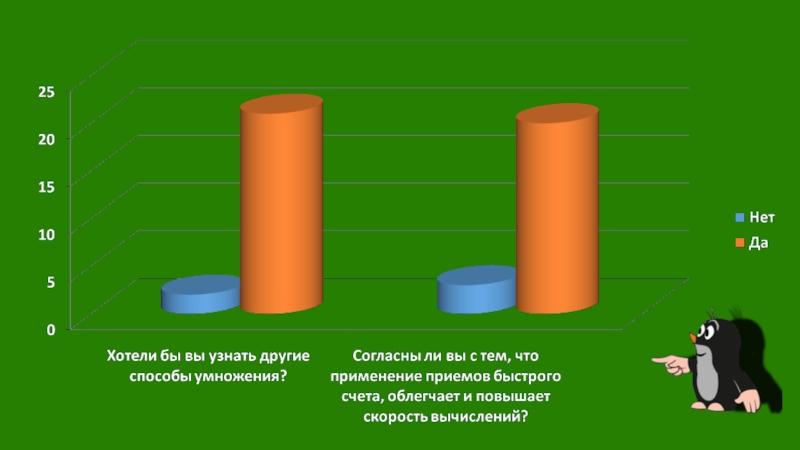
Гипотеза моего исследования: если показать, что применение приемов быстрого счета, облегчает
вычисления, то можно добиться того, что повысится качество и скорость вычислений учащихся, не прибегая к использованию калькулятора.
Актуальность данной темы заключается в том, что использование нестандартных приемов в формировании вычислительных навыков усиливает интерес учащихся к математике и содействует развитию математических способностей.
Актуальность данной темы заключается в том, что использование нестандартных приемов в формировании вычислительных навыков усиливает интерес учащихся к математике и содействует развитию математических способностей.
Слайд 5
Нестандартные способы умножения.
1. Индийский способ умножения.
2. Умножение способом «МАЛЕНЬКИЙ ЗАМОК».
3. Умножение чисел методом «ревность».
4. Крестьянский способ умножения.
5. Новый способ умножения.
Слайд 18
1. Умножение на 11
Умножение на 11 по Трахтенбергу.
Умножение на
22, 33, ..., 99
4. Умножение на число 111, 1111 и т. д., зная правила умножения
двузначного числа на число 11.
Умножение двузначного числа на 101, 1001 и т.д..
6. Умножение на 9.
7. Умножение на 99, на 999.
8. Умножение трёхзначного числа на 999.
9. Умножение на число, записанное одними девятками.
10. Умножение на 5, 25, 125.
11. Умножение на 37.
12. Умножение чисел, близких к 100 и 1000.
4. Умножение на число 111, 1111 и т. д., зная правила умножения
двузначного числа на число 11.
Умножение двузначного числа на 101, 1001 и т.д..
6. Умножение на 9.
7. Умножение на 99, на 999.
8. Умножение трёхзначного числа на 999.
9. Умножение на число, записанное одними девятками.
10. Умножение на 5, 25, 125.
11. Умножение на 37.
12. Умножение чисел, близких к 100 и 1000.
Слайд 20Умножение на 11
«Краешки сложи, в серединку положи» - эти слова помогут
легко запомнить данный способ умножения на 11.
Чтобы двузначное число, сумма цифр которого не превышает 10, умножить на 11, надо цифры этого числа раздвинуть и поставить между ними сумму этих цифр.
Примеры:
72 ∙ 11 = 7 (7 + 2) 2 = 792;
35 ∙ 11 = 3 (3 + 5) 5 = 385.
Чтобы умножить на 11 двузначное число, сумма цифр которого 10 или больше 10, надо мысленно раздвинуть цифры этого числа, поставить между ними сумму этих цифр, а затем к первой цифре прибавить единицу, а вторую и последнюю (третью) оставить без изменения.
Пример:
94 ∙ 11 = 9 (9 + 4) 4 = 9 (13) 4 = (9 + 1) 34 = 1034
68 11 = 6 (6+8) 8 = 6 (14) 8 = (6+1) 4 8 = 748
Чтобы двузначное число, сумма цифр которого не превышает 10, умножить на 11, надо цифры этого числа раздвинуть и поставить между ними сумму этих цифр.
Примеры:
72 ∙ 11 = 7 (7 + 2) 2 = 792;
35 ∙ 11 = 3 (3 + 5) 5 = 385.
Чтобы умножить на 11 двузначное число, сумма цифр которого 10 или больше 10, надо мысленно раздвинуть цифры этого числа, поставить между ними сумму этих цифр, а затем к первой цифре прибавить единицу, а вторую и последнюю (третью) оставить без изменения.
Пример:
94 ∙ 11 = 9 (9 + 4) 4 = 9 (13) 4 = (9 + 1) 34 = 1034
68 11 = 6 (6+8) 8 = 6 (14) 8 = (6+1) 4 8 = 748
Слайд 21Умножение на 22, 33, ..., 99
Чтобы двузначное число умножить на 22,
33, ..., 99, надо этот множитель представить в виде произведения однозначного числа на 11, то есть 44 = 4 ∙11; 55 = 5 ∙ 11 и т.д. Затем выполнить умножение сначала на однозначное число, а потом на 11.
Примеры:
24 ∙ 22 = 24 ∙ 2 ∙ 11 = 48 ∙ 11 = 528
23 ∙ 33 = 23 ∙ 3 ∙ 11 = 69 ∙ 11 = 759
Примеры:
24 ∙ 22 = 24 ∙ 2 ∙ 11 = 48 ∙ 11 = 528
23 ∙ 33 = 23 ∙ 3 ∙ 11 = 69 ∙ 11 = 759
Слайд 22Умножение двузначного числа на 101, 1001 и т.д..
Пожалуй, самое простое правило:
припишите ваше число к самому себе. Умножение закончено!!!
Примеры:
32 ∙ 101 = 3232;
47 ∙101 = 4747;
324 ∙ 1001 = 324 324;
675 ∙ 1001 = 675 675;
6478 ∙10001 = 64786478;
846932 ∙ 1000001 = 846932846932.
Примеры:
32 ∙ 101 = 3232;
47 ∙101 = 4747;
324 ∙ 1001 = 324 324;
675 ∙ 1001 = 675 675;
6478 ∙10001 = 64786478;
846932 ∙ 1000001 = 846932846932.
Слайд 23 Умножение чисел, близких к 100 и 1000.
Например, надо перемножить числа
96 и 97. Найдем вспомогательные числа. Их находим вычитанием данных чисел из 100. В нашем случая получается, что вспомогательные числа это 4 и 3. Дальше можем забыть о данных нам числах. Теперь найдем цифры стоящие вначале необходимого нам числа: мы складываем 4 и 3, а затем получившееся число отнимаем от 100. Получается: 93. Значит в начале нашего числа стоит цифра 93. Затем найдем последние цифры необходимого нам числа: мы просто перемножаем 4 и 3. Получается 12 — это последние цифры нашего числа. У нас получилось число 9312.
96 · 97 = 9312
1) 100-96=4 – вспомогательное число
2) 100-97=3 – вспомогательное число
3) 100-(4+3)=100-7=93 – первые цифры,
4) 4·3=12 – последние цифры.
96 · 97 = 9312
1) 100-96=4 – вспомогательное число
2) 100-97=3 – вспомогательное число
3) 100-(4+3)=100-7=93 – первые цифры,
4) 4·3=12 – последние цифры.